归一化概念
|
MinMaxScaler,最大最小归一化 from sklearn.preprocessing import MinMaxScale (x - min) / (max - min) 将数据映射到[0,1] ,近似于同比映射
|
|
StandardScaler from sklearn.preprocessing import StandardScaler (x - mean) / std 这实际上将数据拉向 均值为0 标准差为1的 标准正态分布 import torch from torch import nn from sklearn.preprocessing import StandardScaler data = [[0, 0], [0, 0], [1, 1], [1, 1]] scaler = StandardScaler() scaler.fit(data) scaler.transform(data)
array([[-1., -1.],
[-1., -1.],
[ 1., 1.],
[ 1., 1.]])
scaler.mean_ array([0.5, 0.5]) scaler.var_ array([0.25, 0.25]) (2-0.5)/0.5 = 3 scaler.transform([[2, 2]]) array([[3., 3.]])
|
在深度学习训练的过程中,数据以0为中心,在[-1,1]之间时,比较容易收敛 转化为标准正态分布的处理,虽然不是所有数据, 但绝大多数还是映射到了[-1,1]之间 这符合了深度学习多层网络训练的需求,大概过程如下: 数据预处理时,做了归一化,在[-1,1]之间, 经过一次神经网络,数据分布就漂一些, 然后标准归一化处理一下,让数据向标准正态分布靠拢一些, 再经过一次神经网络,数据分布再漂一些, 然后标准归一化处理一下,让数据再向标准正态分布靠拢一些, ... ... ... 深度学习中的归一化 同样的计算逻辑,将其封装为一层 每次神经网络处理,数据分布就会跑偏一些, 然后归一处理一下,它就往标准正态分布靠拢一些, 在理论上, 在理论上,会好那么一点点... 问题是,归一处理会不会影响数据中包含的规律, 确切地说,会不会影响数据到指定标签之间的规律? 这个经过多次,或者说很多人的很多次试验证明, 不影响,或者影响可以忽略不计 计算机擅长计算[-1,1]且以0为中心分布的数据,这样的数据不容易分散, 过大容易梯度爆炸, 过小容易数据都消失了, - 数据流过N个网络最终到达标签所在的网络层, - 结果还没到呢,数据就全是0或者几乎不变了, - 或者是一次训练一次改变,结果还没到预期效果呢,数据就全是0了,相当于流不到标签那里就断流了 归一化能很大程序上缓解这个问题 |
- 将数据分布拉到标准正态分布 - 加速收敛 - 一定程度上将数据集中到[-1,1]之间,捎带有统一量纲的作用 |
|
归一化的位置 归一化是为了解决数据分布偏移的问题,通常是经过几次神经网络计算之后 , 比如transformer的每一层中,有以下几步: 1 求补码, 2 编码并按特征维度拆分, 3 矩阵相乘,即线性变换 4 做softmax, 5 求得分, 6 再矩阵相乘,即线性变换 7 层归一化 8 全连接, 9 激活函数处理, 10 全连接 1-7 是一个逻辑,这一通计算后数据分布肯定偏移了,第8步加一个归一化 - 当然了,如果网络简单,可以尝试不要归一化 - 意思是,如果不加归一化的效果会更好,那么就不要归一化 在传统神经网络中,BN在卷积之后,再之后是relu - 如果是这样,BN将数据拉到以0为中心,relu直接抹掉小于0的数据,相当于抹去一半的正态分布 - 但要注意的是,批次数据半不是前半部分为负,后半部分为正,而是正负混合的 - 被抹去的一半负数据,是零散分布于批次数据中的 - 因为经过relu处理,矩阵会零零散散一多出一些0数据 |
BN论文
Batch Normalization论文标题解读
这是论文的标题: Batch Normalization: Accelerating Deep Network Training byReducing Internal Covariate Shift Reducing Internal Covariate Shift 减少内部协变量偏移 加速收敛及减少数据分布的偏移 accelerating英/əkˈseləreɪtɪŋ/ 美 /əkˈseləreɪtɪŋ/ v.(使)加速;加快 数据是有分布的,或者说不管它有没有,统一将数据看作或者默认它是符合正态分布的 数据分布主要有两个衡量指标:分布中心以及其离散程序 深度学习训练不像机器学习那样一次训练就定型,或者网络有很多的层, 多次训练,每次微调模型参数... 再用新的模型参数与数据计算,得到新的分布 一次次训练后,新的分布与原有数据有分布就不一样的,或者说漂移了,这就是论文标题提到的 Internal Covariate Shift 这种分布的改变,过大会导致梯度爆炸, 过小梯度消失,数据很小后,改变量也随之就小...
BN与归一化
本质上BN与归一化算法思路一样,细节上有些差异:BN增加了可学习参数 这个细节设计的来源: - 数据分布改变了,你说这不适合,你想拉回来 - 那拉回来多少合适? - 你就这样要求所有数据回到标准正态分布是否太断武断,是否是一刀切行为? - 如果一刀切了,有些激活函数,比如ReLU直接把小于0的全扔了,这是否合适呢 - 有的神经网络没有把ReLU直接放BN的后面,或者干脆就没用BN,效果也不差 - 你所认为的不适合,只是你认为的,还是实现也的确如此? 解决方法 - 到底是否适合,拉到什么程度,设计成可学习的,由模型的参数通过学习决定 也就是常说的为神经网络赋予某种能力, - 功能给你了,有需要再用,实际不需要时,参数自动学习为0,相当于不用 - 用的时候用几分力,用到什么程度,由实际情况决定
BN核心逻辑

输入是一列的数据中的一个批次, 1 一个x对应一个y 2 求均值 3 求方差 5 映射到标准正态分布,其中分母为了防止为0,加一个微小的数 6 yi = a*xi + b, - a,b是可学习参数, - 如果a=std,b=mean的话,y那么yi就是最开始的xi - 如果a,b是其他的值的,y就是以正态分布为基础,根据数据规律漂移后的结果
图像处理用批归一化的多, 序列处理用层归一化的多
DL的批次
机器学习没有批次的概念,一个批次就是全体数据集 深度学习中有批次的概念,所有的计算都是以批次形式计算的 但有时会用到均值,标准差这些变量,同时要寻找的规律,实现是整个数据集的规律,怎么办? 先求批次的,然后逆推整个数据集的
批归一化(Batch Normalization)
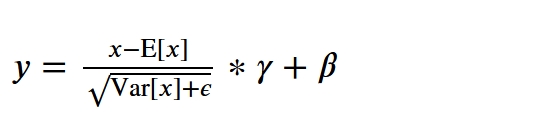
import torch
from torch import nn
# The mean and standard-deviation are calculated per-dimension over
nn.BatchNorm2d()
y = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta
参数num_features:特征数,比如像素的3色,单词的embedding_dim
nn.BatchNorm2d(num_features=3) 如果是2维关系表,对一列做归一化, - 如果是RGB3色的话,就是对[H,W]的数值做归一化 按维度的话,就是对一个维度的特征做归一化
不管原来是什么shape,统一转化为[B,C,L],然后对L做归一化
第一个维度是批次 第二个维度是特征 第三个维度是原特征图展平形成的向量/列表 对于图像[B,C,H,W] -- 将[H,W]展平求归一化 对于文件[B,C,L] -- 直接对L求归一化 归一化:减 均值 ,再除以标准差
取特征维度数据
X表示RGB三色的批次图像数据 X[B,C,H,W] 取第1个特征 X[:,0,:,:] 取第2个特征 X[:,1,:,:] 取第3个特征 X[:,2,:,:]
预测时使用的是训练时批次的均值和标准差
训练是批次的,预测通常是单个样本 单个样本的均值与标准差 浮动过大,不合适用 批次训练时,记录每个批次的均值与标准差,并以此评估整个数据集的均值与标准差 预测使用的是,训练时预测的整个数据集的 均值与标准差 这种思想是伟大的... 即保证了预测与训练的计算过程是一样的,又避免了预测时单个样本均值与标准差浮动带来的波动问题
为什么图像多使用BN(以下仅个人猜测,如有...纯属...)
图像处理用批归一化的多, - 因为图像特征数不多, - 基本就1-灰色,3-RGB,4-RGB+一个透明度, - 特征图[H,W]的元素数据是很多的 - 核心的信息更多在特征图[H,W]中,而不是RGB特征维度中 序列处理用层归一化的多 - 序列中一个单词的维度通常在100-300之间 - 单词个数,即句子长度可能是8,32,64...不等,一句话20个单词就算多了 - 核心的信息更多在单词的维度中,所以才不是像图像那样对特征图做归一化
The mean and standard-deviation are calculated per-dimension over
deviation英/ˌdiːviˈeɪʃn/美/ˌdiːviˈeɪʃn/ n.偏差; dimension英/dɪˈmenʃn/ 美/daɪˈmenʃn/ n.方面;范围;维(构成空间的因素);侧面 The mean and standard-deviation are calculated per-dimension over 核心在于“dimension”-特征维度 均值和标准差是在 特征维度 上计算的
nn.BatchNorm要求特征维度在第2个位置上,即索引为1的维度上
也不是BatchNorm的要求,实际上是torch框架的要求 在torch框架中, 文本等一维数据的shape通常为[Batch_size,特征维度(单词向量维数,embedding_dim),特征shape(单词个数)] 图像等2维数据[Batch_size,C,W,H],特征维数也是在第2个位置上 BatchNorm在torch.nn下面,自然就遵守这个约定,将特征维度放在了第2个位置上
针对一个特征层上的数据分布进行归一化,相当于对库表某列做归一化
import torch
from torch import nn
torch.manual_seed(73)
batch_size = 1
num_features=2
x=torch.linspace(start=1,end=6,steps=6).reshape(batch_size,num_features,3)
x
tensor([[[1., 2., 3.],
[4., 5., 6.]]])
bn = nn.BatchNorm1d(num_features=num_features)
bn(x)
tensor([[[-1.2247e+00, 0.0000e+00, 1.2247e+00],
[-1.2247e+00, -1.1921e-07, 1.2247e+00]]],
grad_fn=NativeBatchNormBackward0)
文本处理举例
import torch from torch import nn data = [[[1,2,3,4,5],[1,2,3,4,5],[1,20,30,400,500]]] embedding_dim = 5 data = torch.tensor(data).float() data.shape torch.Size([1, 3, 5])
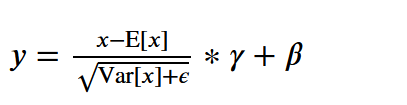
批归一化:特征层必须在第2个维度,公式完全一致
层归一化,归一的是每个元素(比如每个单词)的特征数据,,相当于对库表某行做归一化 批归一化,归一的是每个特征层上的数据分布(所有数据在某个特征维度上的数据),相当于对库表某列做归一化
# 1D要求3维[B,C,L],2D要求4维[B,C,W,H]
data = [[[1,2,3,4,5],[1,2,3,4,5],[1,2,3,4,5]]]
data = torch.tensor(data).float()
data = data.permute(0,2,1) # 这里不要用reshape,这里是交换维度
bn = nn.BatchNorm1d(num_features=5)
# 每个特征层上的数据分布
data
tensor([[[1., 1., 1.],
[2., 2., 2.],
[3., 3., 3.],
[4., 4., 4.],
[5., 5., 5.]]])
bn(data)
tensor([[[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]]], grad_fn=NativeBatchNormBackward0)
层归一化
文本处理举例,1个批次,3个单词,每个单词5个维度
import torch from torch import nn data = [[[1,2,3,4,5],[1,2,3,4,5],[1,20,30,400,500]]] embedding_dim = 5 data = torch.tensor(data).float() data.shape torch.Size([1, 3, 5])
层归一化:标准化 + 可学习参数
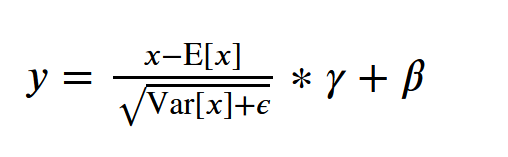
# normalized_shape必须是data.shape的最后一维,将这个维度的数据分布拉到正态分布
# 如果是文本,[batch_size,seq_len,embedding_dim],相当于对每个单词做了归一化
layer_norm = nn.LayerNorm(normalized_shape=embedding_dim)
#400,500相对1是一个很大的数,归一化后,接近于1,
# 这是要将每个元素的数据分布拉到标准正态分布了,有加速收敛的作用
layer_norm(data)
tensor([[[-1.4142, -0.7071, 0.0000, 0.7071, 1.4142],
[-1.4142, -0.7071, 0.0000, 0.7071, 1.4142],
[-0.8813, -0.7928, -0.7463, 0.9773, 1.4431]]],
grad_fn=NativeLayerNormBackward0)
The mean and standard-deviation are calculated over the last `D` dimensions, where `D`
is the dimension of :attr:`normalized_shape`. For example, if :attr:`normalized_shape`
is ``(3, 5)`` (a 2-dimensional shape), the mean and standard-deviation are computed over
the last 2 dimensions of the input (i.e. ``input.mean((-2, -1))``).
:math:`\gamma` and :math:`\beta` are learnable affine transform parameters of
:attr:`normalized_shape` if :attr:`elementwise_affine` is ``True``.
The standard-deviation is calculated via the biased estimator, equivalent to
`torch.var(input, unbiased=False)`.
Shape:
- Input: :math:`(N, *)`
- Output: :math:`(N, *)` (same shape as input)
NLP Example
# NLP Example batch, sentence_length, embedding_dim = 20, 5, 10 embedding = torch.randn(batch, sentence_length, embedding_dim) layer_norm = nn.LayerNorm(embedding_dim) # Activate module layer_norm(embedding)
参数 elementwise_affine
note:: Unlike Batch Normalization and Instance Normalization, which applies scalar scale and bias for each entire channel/plane with the :attr:`affine` option, Layer Normalization applies per-element scale and bias with :attr:`elementwise_affine`. elementwise_affine: a boolean value that when set to ``True``, this module has learnable per-element affine parameters initialized to ones (for weights) and zeros (for biases). Default: ``True``. 批归一化是一个特征层(相当于数据处理时列的维度)一个可学习参数加一个偏置 层归一化是每个元素(相当于数据处理时行的维度,一行多列为一个元素)都有一个可学习参数加一个偏置 elementwise_affine为True时,初始化参数所有值为1,默认为True
归一对比
import torch
from torch import nn
def batch_norm(data):
data = torch.tensor(data).float()
print(data.shape) #torch.Size([3, 5])
# 1D要求3维[B,C,L],2D要求4维[B,C,W,H]
data = data.unsqueeze(1)
#目录仍然是一行一个样本
print(data.shape) # torch.Size([3, 1, 5])
#相当于取data[:,i]作归一化
bn = nn.BatchNorm1d(num_features=data.shape[1])
return bn(data)
#常见2维数表,一行对应一个样本
data = [[1,2,3,4,5],[1,2,3,4,5],[1,2,3,4,5]]
batch_norm(data)
torch.Size([3, 5])
torch.Size([3, 1, 5])
tensor([[[-1.4142e+00, -7.0710e-01, 1.1921e-07, 7.0711e-01, 1.4142e+00]],
[[-1.4142e+00, -7.0710e-01, 1.1921e-07, 7.0711e-01, 1.4142e+00]],
[[-1.4142e+00, -7.0710e-01, 1.1921e-07, 7.0711e-01, 1.4142e+00]]],
grad_fn=NativeBatchNormBackward0)
data = [[5,2,3,4,5],[1,2,3,4,5],[1,2,3,4,5]]
batch_norm(data)
torch.Size([3, 5])
torch.Size([3, 1, 5])
tensor([[[ 1.2480, -0.9120, -0.1920, 0.5280, 1.2480]],
[[-1.6320, -0.9120, -0.1920, 0.5280, 1.2480]],
[[-1.6320, -0.9120, -0.1920, 0.5280, 1.2480]]],
grad_fn=NativeBatchNormBackward0)
一个维度上修改一个数,影响了所有维度上的数据
批归一化针对的是整个批次的数据
|
import torch
from torch import nn
def layer_norm(data):
data = torch.tensor(data).float()
print(data.shape) #torch.Size([3, 5])
# 1D要求3维[B,C,L],2D要求4维[B,C,W,H]
data = data.unsqueeze(1)
#目录仍然是一行一个样本
print(data.shape) # torch.Size([3, 1, 5])
#相当于取data[:,i]作归一化,不同于BN,这里按维度进行了分组,要求需要做归一化的维度放在数据的最后一维
norm = nn.LayerNorm(normalized_shape=data.shape[2])
return norm(data)
#常见2维数表,一行对应一个样本
data = [[1,2,3,4,5],[1,2,3,4,5],[1,2,3,4,5]]
layer_norm(data)
torch.Size([3, 5])
torch.Size([3, 1, 5])
tensor([[[-1.4142, -0.7071, 0.0000, 0.7071, 1.4142]],
[[-1.4142, -0.7071, 0.0000, 0.7071, 1.4142]],
[[-1.4142, -0.7071, 0.0000, 0.7071, 1.4142]]],
grad_fn=NativeLayerNormBackward0)
#常见2维数表,一行对应一个样本
data = [[5,2,3,4,5],[1,2,3,4,5],[1,2,3,4,5]]
layer_norm(data)
torch.Size([3, 5])
torch.Size([3, 1, 5])
tensor([[[ 1.0290, -1.5435, -0.6860, 0.1715, 1.0290]],
[[-1.4142, -0.7071, 0.0000, 0.7071, 1.4142]],
[[-1.4142, -0.7071, 0.0000, 0.7071, 1.4142]]],
grad_fn=NativeLayerNormBackward0)
层归一化针对一个维度,某个维度上的数据变化,不会影响其他维度上的数据
|
|
相同点 [B,C,feature_shape] [B,C,L] 都是对[B,C]的处理,处理方式都是拉到标准正态分布 不同点
层归化一化比批归一化多一次分组
- 批归一化是按C分组,一个C,即一个特征维度上的所有数据取出来做一个归一化
- 层归一化,是按[C,L]分组,先按C分组,然后再按L分组
输入参数不同
- 批归一化,处理的维度确定为第2维C,只需要输入C的维数num_features
- 层归一化,确定为[B,C,L],[B,C,H,W]为B,C之后的维度,但由于不确定是有多少维,所以要输入shape:normalized_shape
import torch data = torch.randn(2,3,4,5) norm = nn.LayerNorm(normalized_shape=[4,5]) norm(data).shape #torch.Size([2, 3, 4, 5]) 层归一化 虽然可以对多个维度进行归一,但必须是data.shape最后的维度 - 可以是最后一维,也可以是最后2维 |
|
|
单位向量化(个人观点)
没见过这种方法,目前看仅个人推测,非官方观点,仅供参考,如有雷同,纯属巧合;
警告,如果你初步接触 统计学,对正统(教材)的基本概念没有深刻的理解,请不要看下面的内容!!! 向量单位化 = 向量/向量的模 向量的模就是 向量的欧氏距离,向量的大小,L2距离, 是各个元素的平方之和再开方, 强调向量本身的长度,向量/向量本身的长 才归于1 而方差呢,方差有两个重点: 1. 每个元素 - 分布的均值,强调分布的中心 2. 平方求和,再除以样本个数,是个平均值 如此, 方差强调的是 整个分布 相对分布中心 的离散程度, 标准差就是整个分布相对分布中心的离散长度(距离或大小) 每个元素-分布均值=每个元素离分布中心的长度(距离或大小) 二者相除,就得到一个分布离散比 从物理学的角度看,就是,要比较两个事物的不同,可以看看两个事物的密度... 方差的侧重点,并不是统一量纲, 而向量单位化则是让任何一个向量100%变化模为1的单位向量,100%的统一量纲 此时向量之间的差异,完全由其夹角体现, 夹角所体现出来的差异性, 个人感觉(就是本人目前没有能力也没时间用数学严格推导证明(就是一疲惫不堪的上班族...)), 要比 纯距离的 分布离散比 有更强的表达能力,带有更多的信息...
批归一化或层归一化LayerNorm(LayerNorm中的layer就是指特征层), 它并不是将矩阵中向量的模归于1,而是 将分布 按数据的 每个特征层都拉向一个正态分布
交叉熵
import torch
def entorpy(x,label):
"""两个概率分布越接近其交叉熵越小
"""
# 转tensor
label = torch.tensor(label)
x1 = torch.tensor(x)
# 熵计算
# log0是负无穷,
# torch.log(torch.tensor(0.)) = -inf
# 为了避免出现此情况,为向量加上一个极小的数,通常是1e-6
x1 = x1 + 1e-6
entorpy = -label*torch.log(x1)
return entorpy.sum()
label = [0,0,1]
x1 = [0.7,0.1,0.2]
print(entorpy(x1,label)) # tensor(1.6094)
label = [0,0,1]
x1 = [0.02,0.06,0.92]
print(entorpy(x1,label)) # tensor(0.0834)
label = [0,0,1]
x1 = [0,0.0001,0.9999]
print(entorpy(x1,label)) # tensor(9.9008e-05)
模型输出分布与标签分布
交叉熵是衡量两个分布之间的差距 在AI中通常使用one-hot编码对标签进行编码,比如 [ [0, 0, 1] [0, 1, 0] [1, 0, 0] ] 对于某个样本,比如[0, 0, 1] 中的三个元素,每个元素的位置代表的是一个类别 ,[0, 0, 1] 则表示第3个类别 从概率的角度讲, [0, 0, 1]是第1类别的概率是0 [0, 0, 1]是第2类别的概率是0 [0, 0, 1]是第3类别的概率是1, 同时0+0+1 = 1,满足概率所有事物可能之和为1的条件 所以[0,0,1]是标签的分布,同时也是其概率分布 模型输出 对于第3个类别,模型输出[0.1, 0.3, 0.7]则表示该样本 在第1类别的输出是0.1,它的目标是0 在第2类别的输出是0.3,它的目标是0 在第3类别的输出是0.7,它的目标是1 或者是干扰因素多,或者是模型不够好,或者是还没有优化到极限, 总之,它现在输出了[0.1, 0.3, 0.7] 它是模型输出的分布,但不是其概率分布 0.1+0.3+ 0.7=1.1
模型输出转概率
import torch # 转概率 label = torch.tensor([0,0,1]) x1 = torch.tensor([0.1,0.3,0.7]) x1 = torch.exp(x1)/torch.exp(x1).sum() + 1e-6 print(x1) # tensor([0.2473, 0.3021, 0.4506])
模型输出是转成概率了,但有两个问题: 1. 对于第3个类别,模型在通过参数调整试图逼近标签,到0.7了,结果转了概率后变成了0.4506,离标签更远了 2. 标签由于是one-hot编码,[0,0,1]前两类是0,算了相当于没算,因为0乘以其他数还是0 工程上优化方向思考: 1. 针对概率变小的问题,a=x-min(x),a/max(a),可使最大索引位置的数值化为1,更符合分类问题的处理方式 2. 不做概率转化,只计算标签[0,0,1]中第3类位置上的数据, 即只计算标签为1的索引位置上的数据, 这里标签永远是1,模型输出则是0.7,|1-0.7|=0.3 计算代价最小,关键是这么做有实际效果吗? 经实践验证是有的,并且效果不差
参考
神经网络】神经元ReLU、Leaky ReLU、PReLU和RReLU的比较