集合与组合
从排列组合的角度来看,事件A与事件B同时发生的概率 P(AB) 可以通过以下方式解释: 1. 样本空间的概念 首先,我们定义一个样本空间 S,它包含了所有可能的基本事件(或称为样本点)。 每个基本事件都是实验的一个可能结果。 2. 事件A和事件B的样本点 事件A:是样本空间 S 的一个子集,包含了所有使得事件A发生的基本事件。 事件B:同样是样本空间 S 的一个子集,包含了所有使得事件B发生的基本事件。 3. 事件A与事件B的交集 事件A与事件B同时发生,即事件A和事件B都发生, 这对应于这两个事件的交集 AB(或写作 A∩B)。 交集包含了同时属于事件A和事件B的所有基本事件。 4. 概率的定义 在概率论中,一个事件的概率是 该事件包含的样本点数与样本空间总样本点数的比值。 如果事件 E 包含 n(E) 个样本点,而样本空间 S 包含 n(S) 个样本点,则事件 E 的概率为: P(E)=n(E)/n(S) 5. 事件A与事件B同时发生的概率 根据上面的定义,事件A与事件B同时发生的概率 P(AB) 就是 交集 AB 包含的样本点数与样本空间总样本点数的比值。即: P(AB)=n(AB)/n(S) 这里,n(AB) 是同时属于事件A和事件B的基本事件的数量,而 n(S) 是样本空间的总基本事件数量。 6. 注意事项 如果事件A和事件B是独立的,则 P(AB)=P(A)×P(B)。 但从排列组合的角度来看,独立性并不是这里的重点;我们只是在解释 P(AB) 的基本概念。 在实际应用中,计算 n(AB)、n(A)、n(B) 和 n(S) 可能需要具体的排列组合技巧或公式。 综上所述,从排列组合的角度来看, 事件A与事件B同时发生的概率 P(AB) 是 交集 AB 包含的样本点数与样本空间总样本点数的比值。 |
学术性的东西,比如数学中的集合,统计学中的集合, 皆是先假设你有了一个全集,这就相当于你是某方向的全知, 你先是全知/先有全体,然后再去研究个体之间的组合... 现实中,一个人初入一个领域,刚刚接触一个东西,不是全知,也很难去收集一个领域的全体 通常都是组合在做这样的事 基本上都以以局部推理全体,甚至直接假定自己知道的就是全体,有点说着说着自己就深信了 然后去印证一些东西,结果印证出来的东西...效果不怎么好... 但回想一些规律的发现,的确有一些是凑齐了全体...而后在个体方向有所突破的 比如, 一个硬币抛了上万次的实验,只是去印证抛一个硬币出现一面的可能 真的是 二分之一 又比如有人真的去收集了百万张图片才去训练一个简单的神经网络... 结果这个神经网络展现了不可思议的效果... |
|
|
|
|
|
|
计数
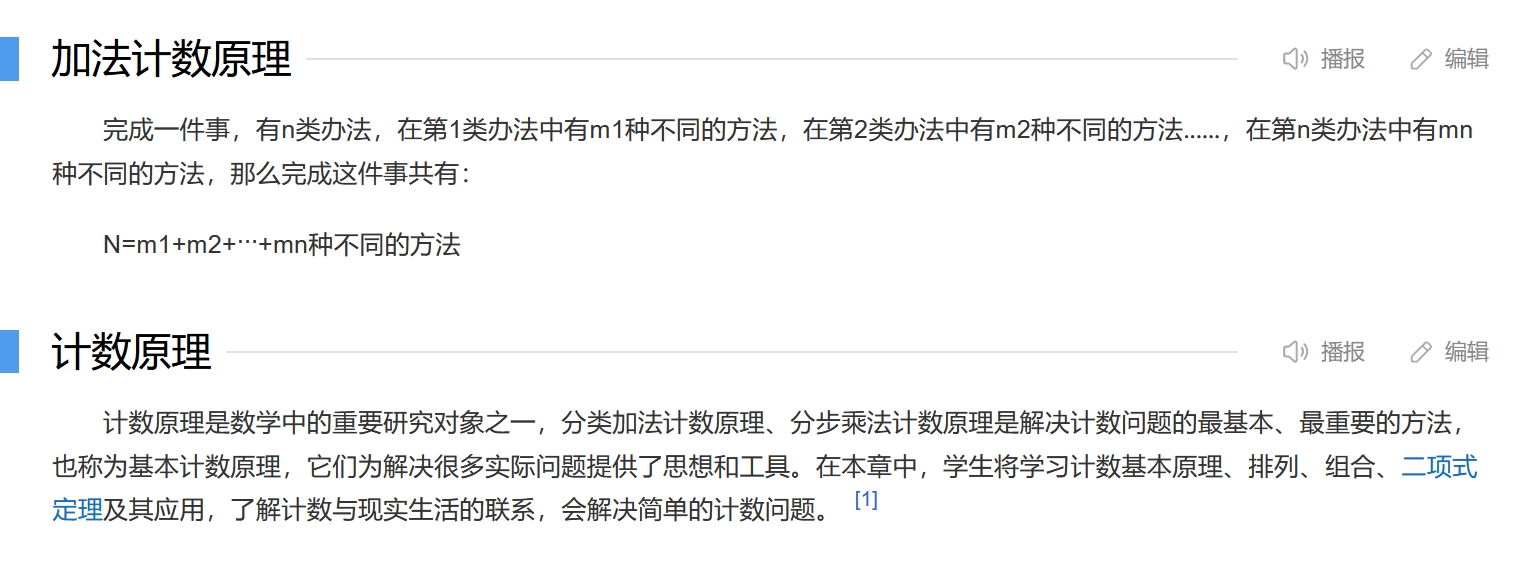
计数,就是 数 数,数一数 事物/事件 的个数,就这么简单 简单不足描述 数 数 这个事情,因为它太底层,有很多的理论是以此为基础的 比如说,统计学中的统计,说白了还是 数 数, 统计概率,就是通过数数算一算概率 比如,有RGB红绿蓝三个小球... 任取一个小球,为红色的概率是多少 1. 数一下总共有多少个小球,共有3个 2. 数一下红色小球有多少个,共1个 那么红球的概率为 1除以3 = 1/3 条件概率 条件:只计算绿球与蓝球 A 求概率:取蓝球的概率 B 即在 只有绿球与蓝球的情况下,取一个球,该球是蓝球的概率 P(B|A) = P(取到蓝球|只有绿球与蓝球) = 蓝球的个数/(蓝球与绿球的总个数) = 1/2 求单词概率 有一篇文章,嗯,就是“有一篇文章”这五个字,指代一篇文章 求“一篇”,“文章”等单词的概率 还是数 数, - 先把文章分词,数一下总单词个数,“有”,“一篇”,“文章” ,共3个 - “文章”的个数为1,那么“文章”出现的概率为 1/3 - “一篇”出现的概率为1/3 求 “文章”这个单词跟在“一篇”这个单词后的概率 这就是后面要说的条件概率,AI中都是条件概率 这里知道,概率是 数 数 来的就可以了 |
|
|
|
|
|
|
|
概率·小小说
概率指一件事发生的可能的大小 概率是确定的,频率在概率附近波动 概率在[0,1]之间 事件A发生的概率可以记为P(A) 条件概率:在一件事A发生的前提下另外一件事B发生的概率 P(B|A) 表示事件A发生的前提下B发生的概率 概率描述的是事件发生的可能性 的大小 是一个数值 该数值是 可能性的度量 ,比如1/2 是数值,有大小,并且还是规律性质的,是固定的,就可以代入数学公式进行计算 进而可以在此基础上,通过数学公式 衍生出其他概率相关的概率 |
|
第一章·生死之门 一老道为探索一个宝藏,提前捉了几十个凡人,供其探路, 最后一关为生死二门,一生一死,此时,凡人也只剩下了最后一个 此人名叫刘老二,此他战战兢兢地走进了老道为他随手一指的门中 踏入此门,入眼是一个昏暗的世界,荒芜,贫瘠,了无生机,脚下是一条泥泞不平的土路, 刘老二心想自己应是踏入了死门, 走在此路上有一种苦燥,孤寂之感,简单的世界,不断的重复,唯已前行... 在他走了一段时间之后, 发现身体越来越舒服,之前辛劳打工留下的胸痛之症消失了,弯曲的腰也慢慢直了起来, 其内心越来越安定不再紧张了 “这是生路”这个想法突然就跳了出来... 此想法一经出现,刘老二思维慢慢地活跃了起来, 他回想起了自己的一生,年少无知无觉随父母流浪, 后来发奋图强想为自己在这残酷的世界求一条生路,结果发现努力好像也没改变什么... 再后来为了讨个生活折了腰... 直到不久前被这老道捉来探路,身边一个个探路者不断地死去,自己现在是最后一个... 刘老二本来也认命了,就这样吧,哪怕自己不被宝藏的风险杀死,最后也会被老道灭口! 但受生门影响,刘老二思维活跃之后,发现了一个可以灭杀老道报仇的机会... 生死二门,一生一死,若自己所在门为生门,那么另外一门必为死门, 入门前,老道为自己简单制作一个命牌,人死牌碎... 若自己死在这里,老道必然会认为这是死门,那么老道会踏入真正的死门... 以自己必死之身,拉一位修道者陪葬,怎么都是赚得! 自己一生卑躬屈膝,死时能拉一位寿数达到千年的修道者陪葬,这一生也是值的! 那毕竟是千万人中才会出现一人的修道者! 此想法在刘老二脑海中反复翻转,并且越来越强,刘老二眼中流出决然之色, 随手捡起路边一截枯枝,狠狠地插进了自己的喉咙... 第二章·死前顿悟 老道发现刘老二命牌碎了之后,未作多想,就跨进了另外一个门中, 他一路就是这么走过来的... 进入死门,眼前呈现的是一片繁花盛世... 花香鸟声悦,人们谦虚礼让,津津乐道,有吃不完的食物,住不完的房子,且都是免费的... 人们再不会因为资源不足而争抢了;老道心中一安,道:“果然是生门” 走着走着,不知道怎么回事,心中开始有一丝不安生起,这生门好的有点过分了! 再细看这些 和颜悦色的人与动物,发现他们慢慢开始变成猛兽,不断向自己靠近... “怎么可能?!”老道失言道,“老刘二...他...以自己的性命为我布了一局...凡人不都是贪生怕死吗?!” 没有给老道太多的时间思考,猛兽已经攻击到了身前,老道也开始恐惧,开始拼命自救... 但这是死门,老道渐渐明白今日自己必死, 知道这一点无法改变之后, 老道的心也渐渐安静了下来,脑海中不禁中开始回往自己的一生... 人生而无知,以无知入世,会被自己的环境困住,这环境一层之外还有一层,层层相扣无穷尽也... 自己悟性在千万人中都是独一无二, 10岁求于道,历经千难万险,斩羁绊,破囚笼,于50岁半百之年跨入修道第一步,获得千年寿数 自己能在50岁入道,很大原因在于明白了 道是道,心是心,道不随心转,求道须舍弃自己的妄念! 要尊重规律,实事求是! 自己10岁就明白这个道理了,又后经40年刻苦学习,甚至不择手段,一心向道,终于在50岁时入道! 这么多年来,一直在压制由心而生的各种念头,一经出现就立刻灭杀, 像什么爱情之类,自己从不触碰...那...会...影响自己求道! 在而后的数百年中,自己不断探索这世界的真相,追求本质,抑制内心, 活得好像没了自己... 像个机器! 但也发生众多的规律!这些规律的确不以人的意志为转移,老夫没错! 只要按规律办事,人怎么想的,根本不重要! 凡夫者,蝼蚁! 第一步修道者,有千年寿数,现在自己已经900多岁了, 要不是寿数将尽,也不会来探索这九死一生的宝藏了! 现在自己终于还是要死了么? 自己这次是如何陷入这次死局的? 事先自己为探索这次宝藏已经准备了100年,明明有很大把握才对,哪里出了问题? 对了,是刘老二,凡夫本应该是怕死的,但在极端的情况下,也有可能不怕 物极必反!自己漏算了这一点... 也就是,要百分之百做成一件事,那么必定要 集齐一件事形成的所有条件, 漏算哪一个,就有可能出问题! 想到这里,老道心中开始有一种明悟,如何跨入修道第二步, 修道第一步是认识到世界的运转依赖的是规律,而不是人心,只有掌握规律才能更大强大 修道第二步是明白事物之间的联系, 万物有联系,没有孤立的存在,或者说如果一个存在是孤立的,那么它就不会被发现 第二步的关键在于以一个规律为中心,找到与它相关的所有规律,以点成面, 成为一个领域的专家,如此才能突破第一步,踏入第二步 初步入道,觉得自己够强了很多,进而陷入对规律的盲目追求之中, 看见这好,就去研究这个,过几年又看见那强,就舍弃了当前的研究,转而研究那个... 会的好多,知的道也不少... 但都是一个个孤点 一念至此,老道开始将心中有联系的点,依据他们自身的特性,开始不段地组合... 以点成线,多个线段反复断开重接,慢慢地有一个圆环诞生了, 该圆环中 各个点相互作用,循环往复,生生不息... 老道身上开始散发出第二步的气息,如果给再他一点的时间,必定能踏入第二步 第二步则有百万年的寿数... 但当下是死门... 数百年来,老道的心早已坚如磐石,早已看淡生死, 这生死有别人的,也包括自己的,除了一开始的惊慌无错,之后心就慢慢平静了... 朝闻道,夕死,足矣!老道就此归去... 全剧终!没有第三章了,本人要去上班了... 尾言 第一步指概率, 一件事物的发生的可能的大小 叫概率,不由心,概率是规律,是不变的, 概率是客观规律,生死二门,我若为生,他则为死,规律不以人的意志为转移 第二步就是指条件概率, 更重要的是 研究明白一件事物发生的环境,有哪些条件,也就是条件概率 提前条件不一样,事件发生的概率就可能不同,甚至是生死逆转 好像自从高中毕业就再没像现在这样写作了... 理科生写的小作文怎么样,有没有 荒诞,胡说八道,乱七八糟的感觉... |
P(AB)表示事件A与事件B同时发生的概率 事件A与事件B要同时发生,那么就必须有交集,否则 P(AB)的值为 0 |
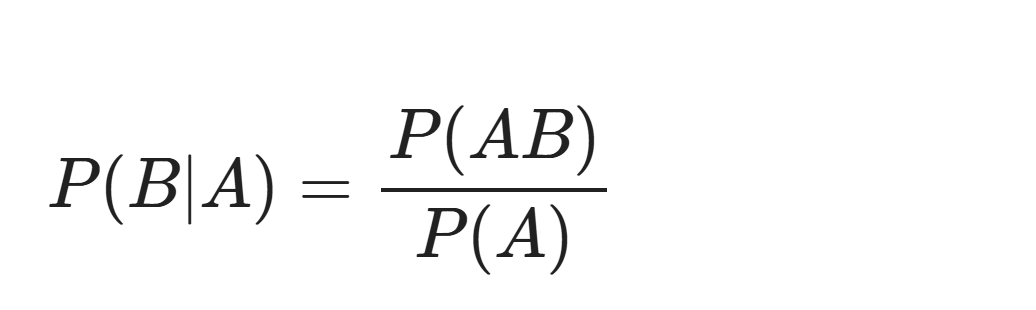
|
|
|
条件概率
五张卡片,共有 3个A,4个B 每张卡片最多一个A,最多一个B P(A)发生的概率 = A的卡片数/总卡片数 = 3/5 P(B)发生的概率 = B的卡片数/总卡片数 = 4/5 P(AB)发生的概率 = AB卡片数/总卡片数 = 2/5 P(B|A) = 包含A的卡片中B的卡片数/A的卡片数 = 2/3 |
|
|
|
|
|
|
|
|
最大似然估计
先验概率与后验概率,似然概率与条件概率,贝叶斯,最大似然估计(MLE)与最大后验概率估计(MAP) https://blog.csdn.net/weixin_40701016/article/details/96484479 详解最大似然估计(MLE)、最大后验概率估计(MAP),以及贝叶斯公式的理解 https://blog.csdn.net/u011508640/article/details/72815981 |
估计 就是 评估 ,尝试计算,认为... 似然,likely,可能性,很像,好像... 似然估计,就是可能性评估/计算 最大似然估计,最大的可能性计算 ,即最大概率计算... 不知道一个事物是什么样的,那么就先默认它具有同类事物中最大可能的样子 生命的本能反应,生活习惯,就是按 最大似然估计而来的 一个稳定的系统/环境,遇到的人与事,都是高度重复的, 连说的话,都会省去大背景,不会每次说话都加上大背景,默认听的人都懂 ... 这是以最小的代价进行各种活动... 不好的影响是,会有小概率的误会,意外发生...能应对就好... 比如,每天早上起床时,身边的一切跟昨天睡觉时差不多... 今天要吃的饭,经历的人,跟最近一段时间经历的差不多 所见,人还是两条腿的多,大地还是大地,天空还是天空, 这世界有无限的信息, 但改变的不多,或者说很缓慢... 所以,当谈到一个你没见过的人的时,你默认他是两条腿, 不会主动问一句,“你说的那个人是两条腿吗?” 这就是本能默认,这就是最大似然估计 不知道一个事物是什么样的,那么就先默认它具体同类事物中最大可能的样子 |
|
|
|
|
|
|
概率密度图
|
概率密度函数 
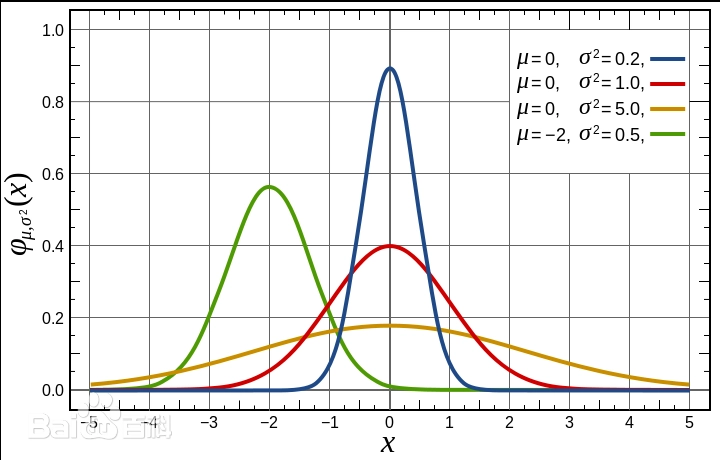
概率(分布)函数 
这里说的分布指概率分布,指的是事物的概率, 事物本身太多,基本不可计数,没有一个固定图形,或者说万物有万形... 即,没有一个公式能表示万物的形状... 但...事物的概率的分布是有规律的,概率的密度分布有是有函数公式的 啥规则? 简单说,常见的事物,它出现的概率就大,少见的事物概率就低...像 是 废话,但 是 真理! 世界是连续,至少从目前这样认为没有什么冲突的地方... 人们看世界是离散的,通常要采样,因此计算的数据全部是离散数据 f(t)在从负无穷到正无穷的的变量x上的积分就是原函数-概率分布函数 在现实世界中,当“数据量达到一定规模”,足够大的时候,都是正态分布函数, 正态就是常态,即常态分布,... 以“常”为“正” 但大多时候,很难收集足够多的数据,但也自认为,即默认我们的数据符合正态分布... 参考 https://baike.baidu.com/item/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%83/829892?fr=ge_ala |

在数学上,概率密度图为 概率分布函数的 导函数 反应的是 概率的变化趋势 x轴代表 连续数据的 分布范围,即 负无穷至正无穷 密度,旨在说明 概率多的数据所集中的区域 即y轴并不是概率,而是概率分布函数的导函数值, 概率密度图中的面积,才是概率 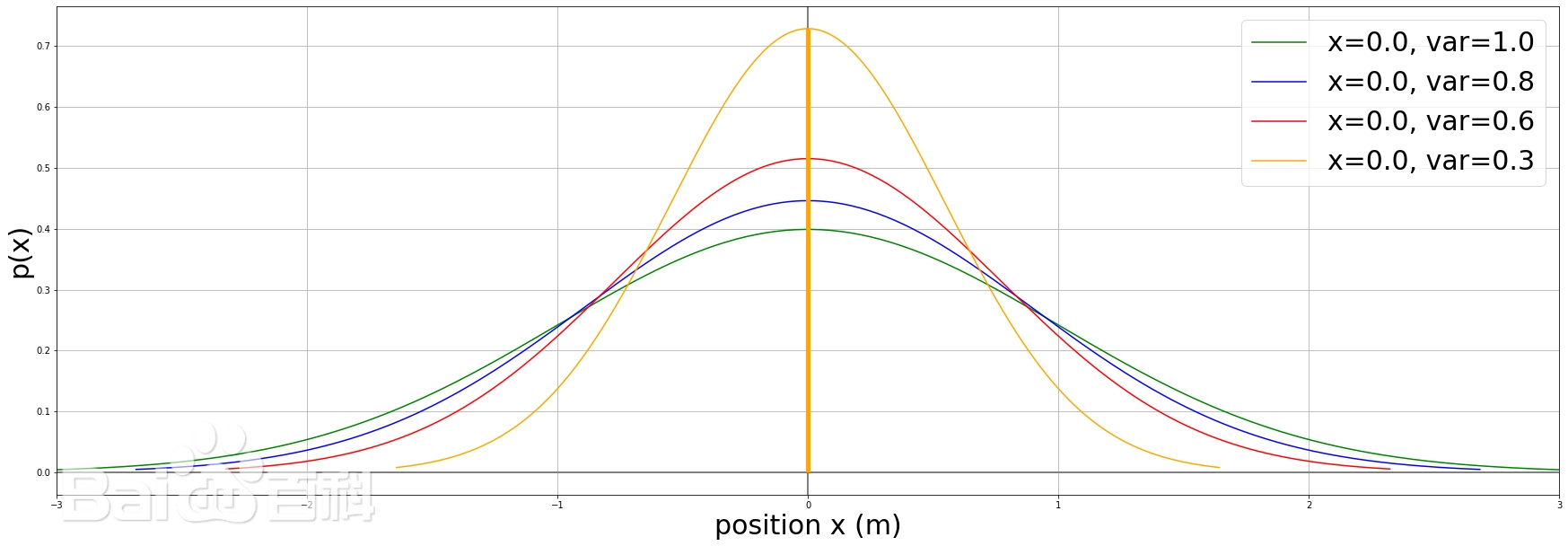
|
|
概率密度函数(Probability Density Function, PDF)的定义 概率密度函数 f(x) 是一个非负函数, 它描述了连续型随机变量 X 在某一特定值附近的概率密度。 具体来说,对于任意实数区间 [a,b],随机变量 X 落在这个区间内的概率为: 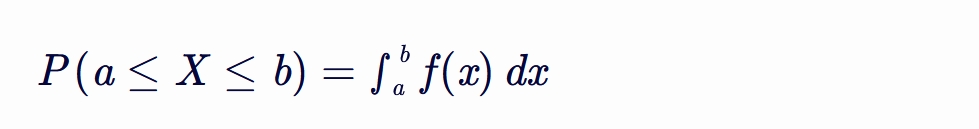
物理上的密度 = 质量/体积 密度大表示集中,俗语说 瓷实... 概率的密度大,就表示某个概率出现的集中 这里再强调一下, 概率是定值,比如抛出一枚硬币出现正面的概率是1/2,是固定的 频率是变的,在概率附近上下波动(数据量大的前提下,就是正态分布时) 概率是体现的是规律,是固定的, 出现的比如集中/稀疏,是指 比如标准正态分布中,数据都集中于0附近 x=0的概率,即P(x=0),密度就很大,有多大?那得看数据的分布了 可以根据概率密度函数进行计算 根据概率密度函数的定义,随机变量 X 落在整个实数域内的概率应为 1,即: P(−∞≤X≤+∞)=1 x轴上的数是不重复的, 比如,x=0只有一个位置,一个点, 但一个以0为中心的分布中,0附近的数据是相当多的,要比其他数据多, 在概率密度图上表现为x=0附近的概率密度最大 注意,我用了“附近”这个词, 概率密度的意义在于表达 一个范围内的概率的大小, 而不在于具体看某个点的概率是多大 概率密度函数形成的曲线与x轴之间的面积, 比如,x属于[a,b]之间的面积,是x出现在[a,b]范围内的概率 
|
AI 第一步,就是要将具体的业务转化为一个数字集合 第二步就是做归一化,向量的模型尽量归于 1 1与1本身不管相乘多少次还是1... AI不注重距离/长度,注重差异, 还有什么能比概率,即百分比 更能体现 差异 呢? 没有了 同时,计算机擅长计算[0,1]之间的数,这与概率不谋而合 万物何其多, 其 概率 密度 用一个公式就可以概括, 而AI正是要计算万物的规律的... 所以,概率在AI的应用非常广泛 补充一下,应用广泛不代表学AI就必须把概率统计学好了, 要先学 线性代数,再学概率... 概率了解就行了 |
|
|
参考