概述
图深度学习 2021年电子工业出版社出版的图书 https://baike.baidu.com/item/%E5%9B%BE%E6%B7%B1%E5%BA%A6%E5%AD%A6%E4%B9%A0 有些数据以图的形式展示更好 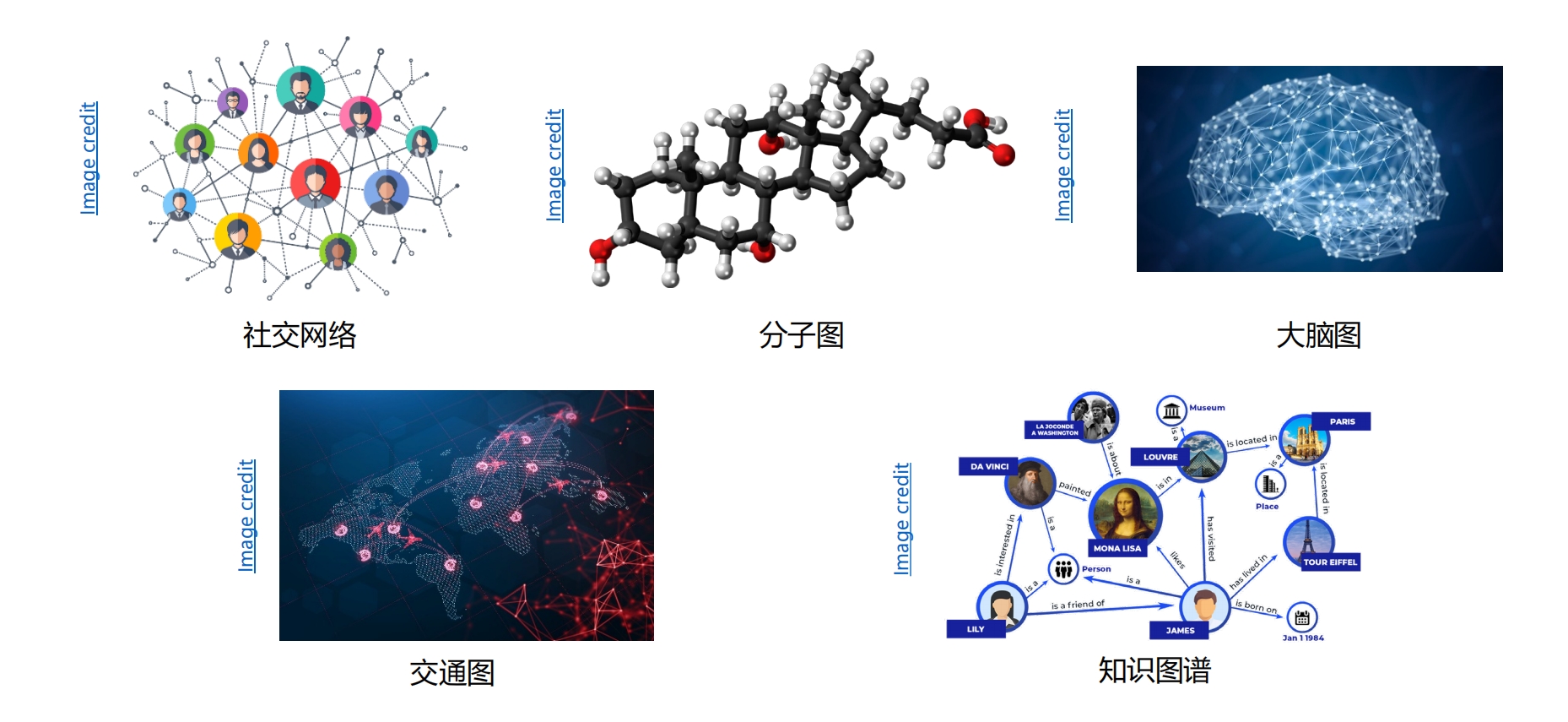
其他数据可以转为图形式 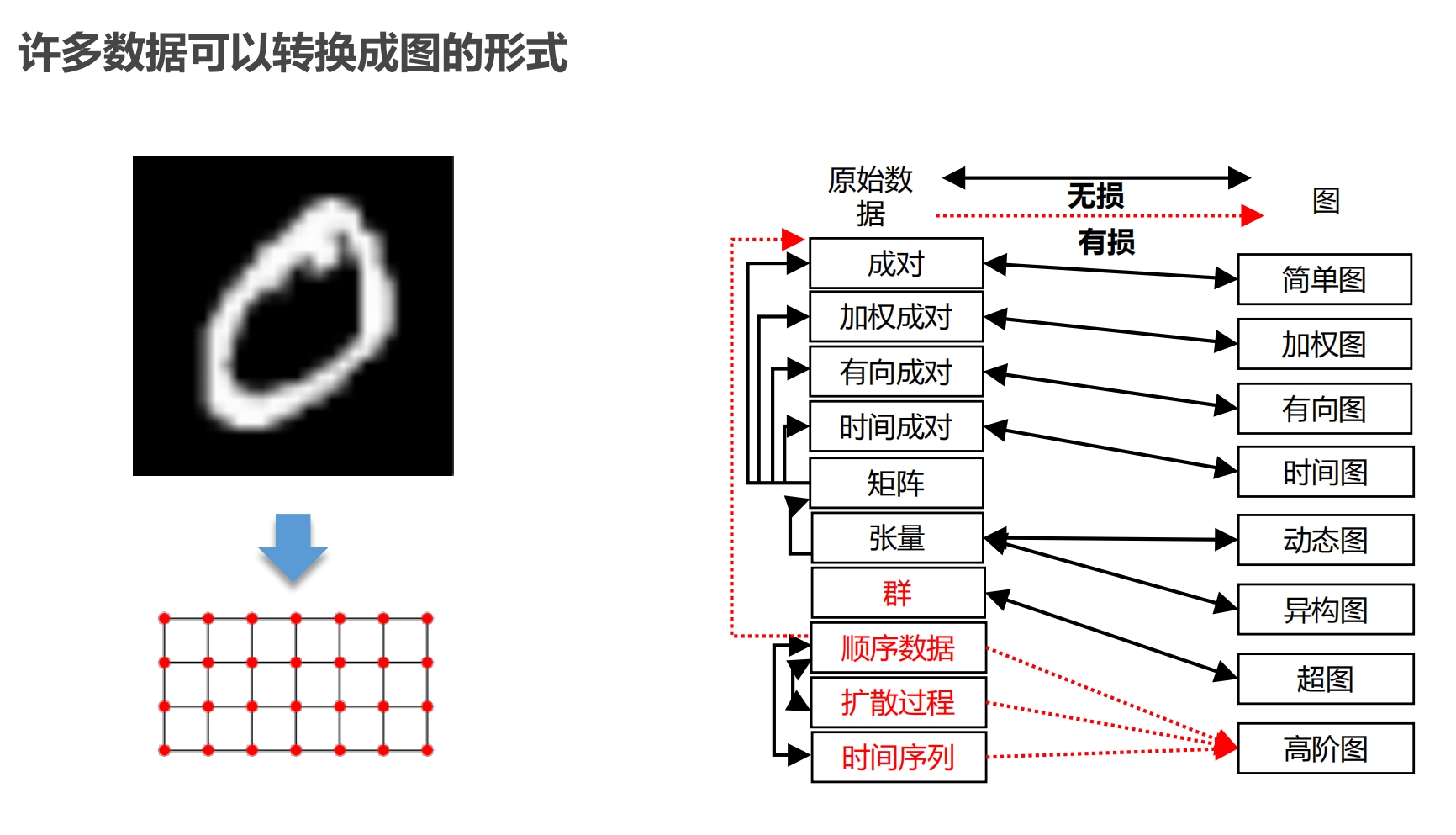
像素为节点,相邻像素为边 顺序数据转图数据会有损失,但这种损失可以忽略不计 |
|
节点之间关系预测 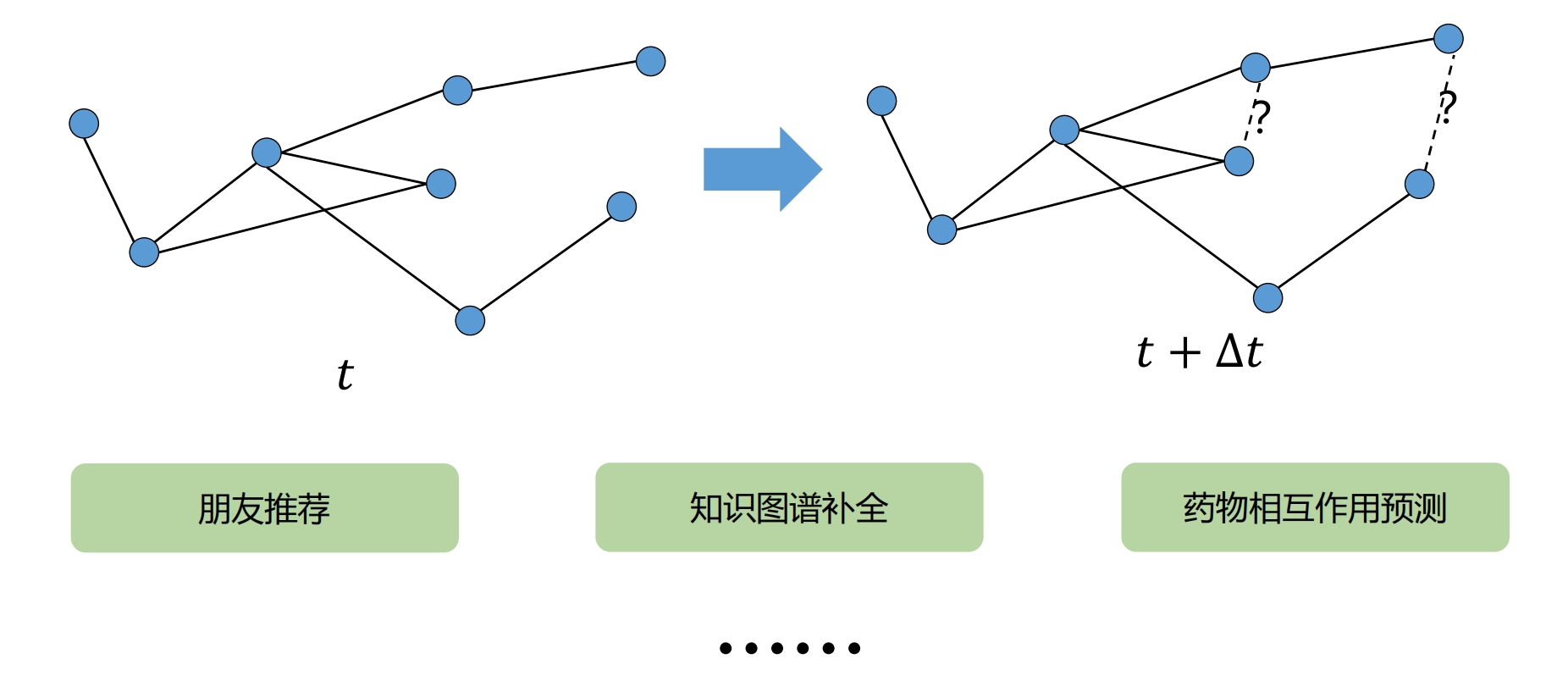
节点分类 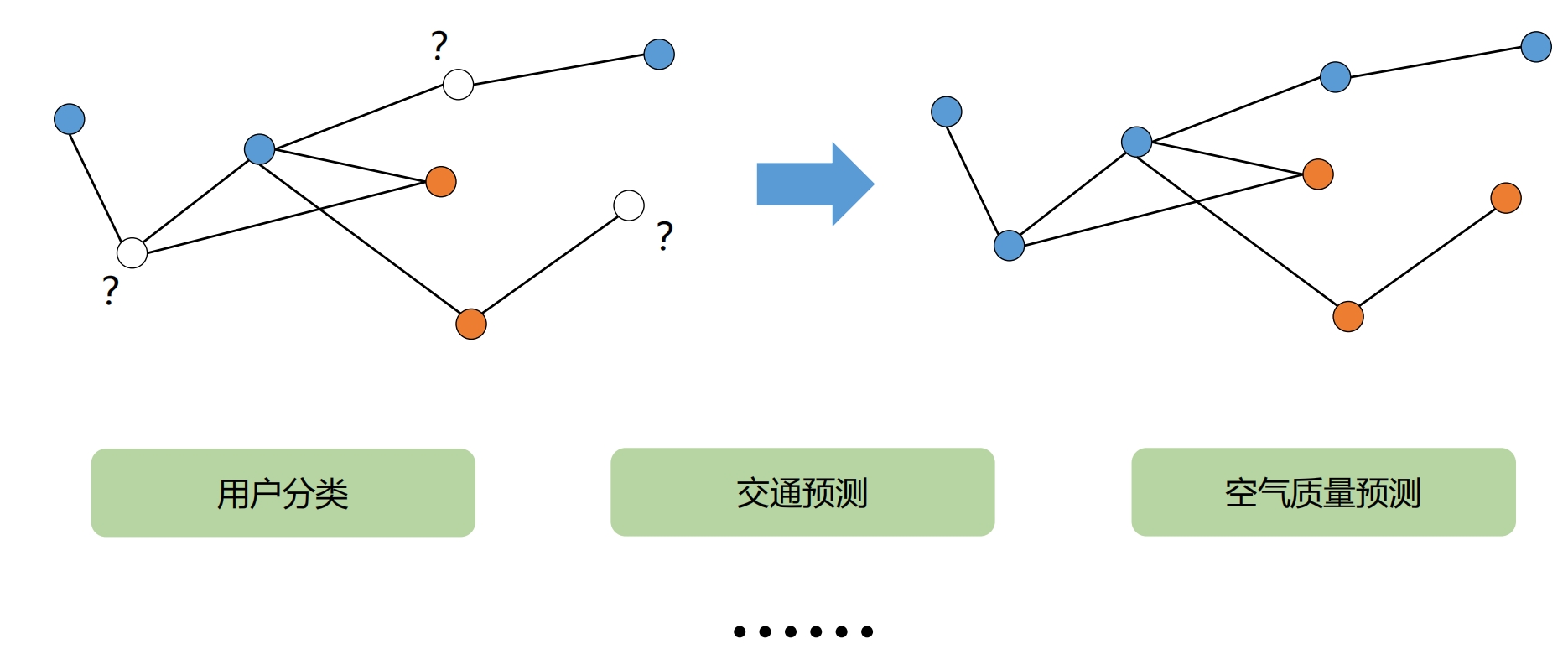
上面 - 每个节点是一个事物,事物之间的关系是图 下面 - 每个数据就是一个图,比如分子结构,分子本身就是图 - 图的生成,匹配... 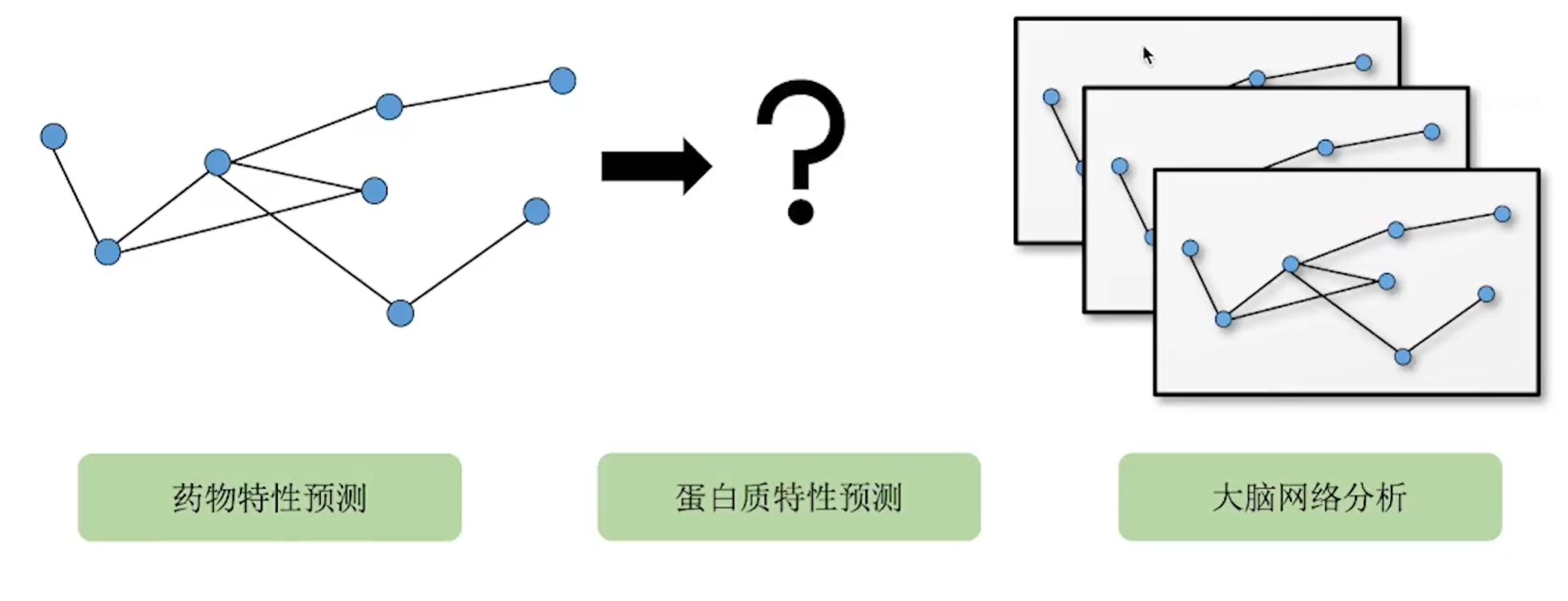
|
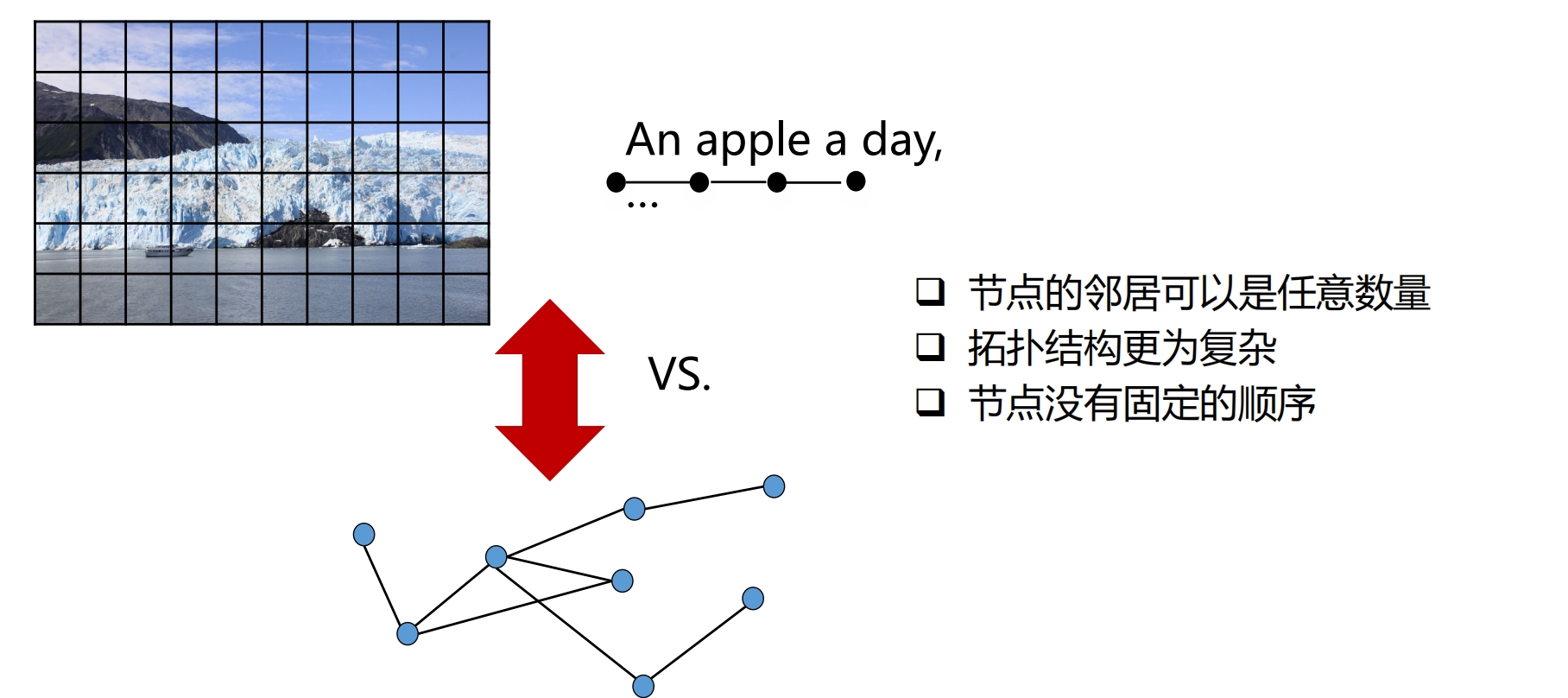
比如,抖音 粉丝 数量,有人几个,有人几万个
因为,深度学习与图的结合,需要依据特定的业务场景进行分析,
下面就列举几个场景
推荐系统 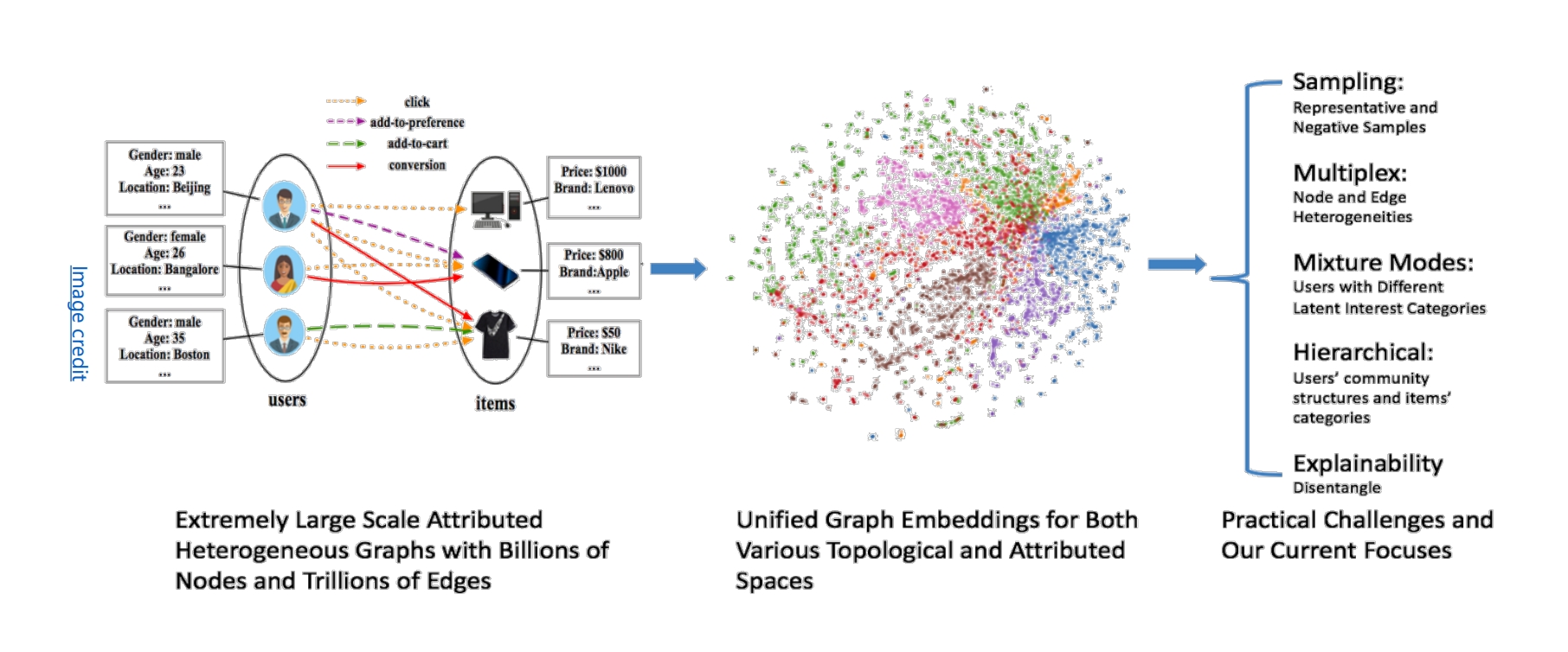
用户,商品为节点
用户的信息可以表示为节点的属性
推荐系统的核心是 学习用户与商品之间的关系
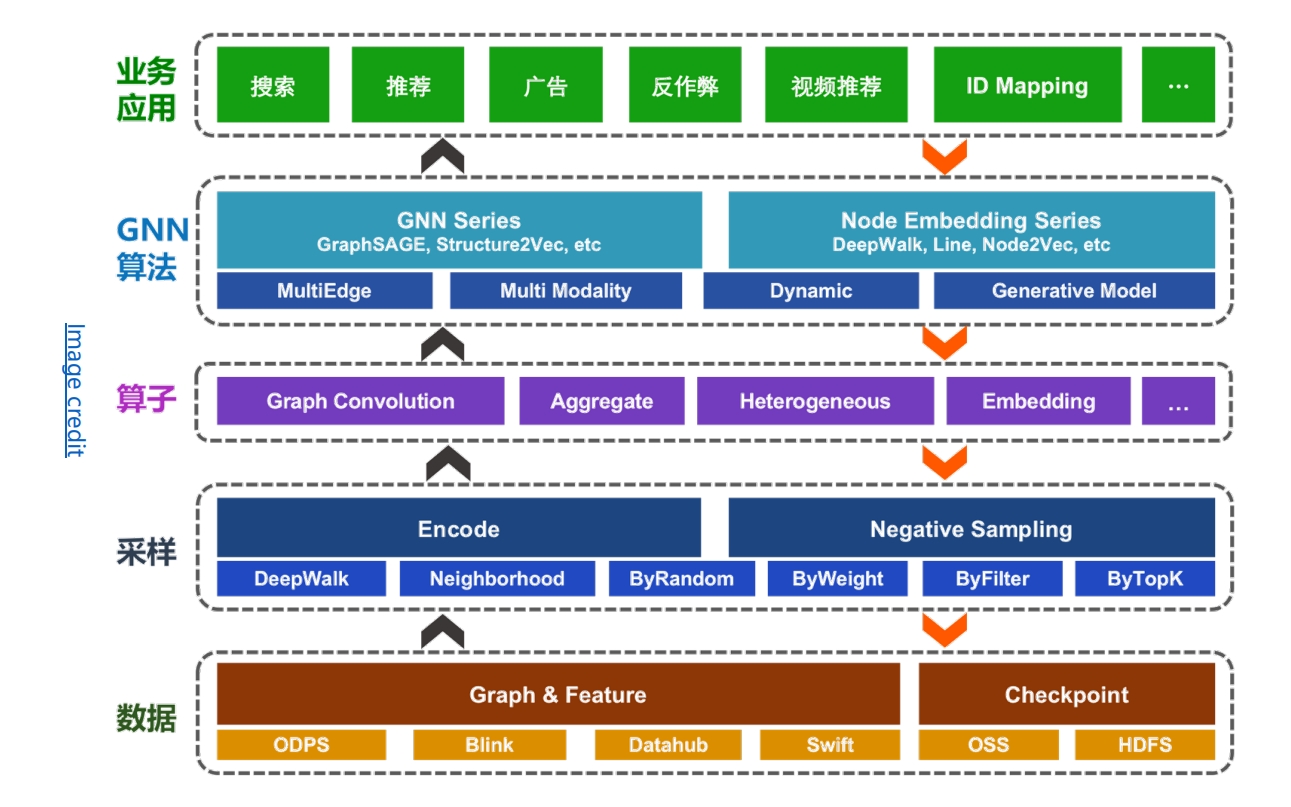
交通预测
Traffic prediction with advanced Graph Neural Networks
https://deepmind.google/discover/blog/traffic-prediction-with-advanced-graph-neural-networks/
路段作为节点
路段之间的关系为边

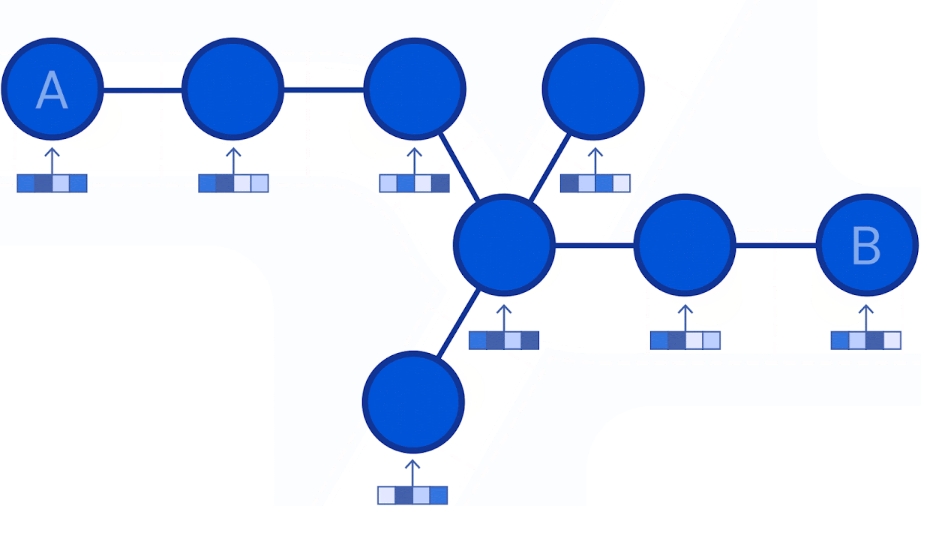
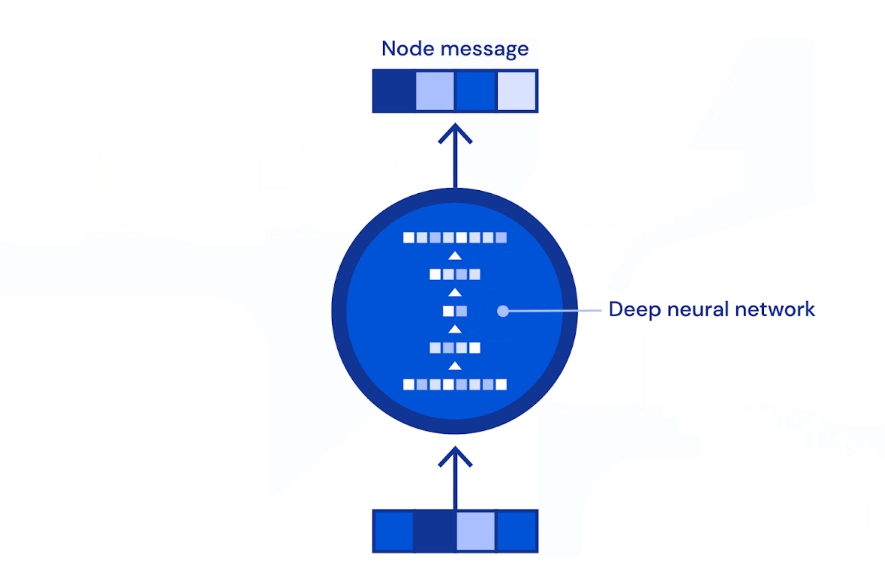
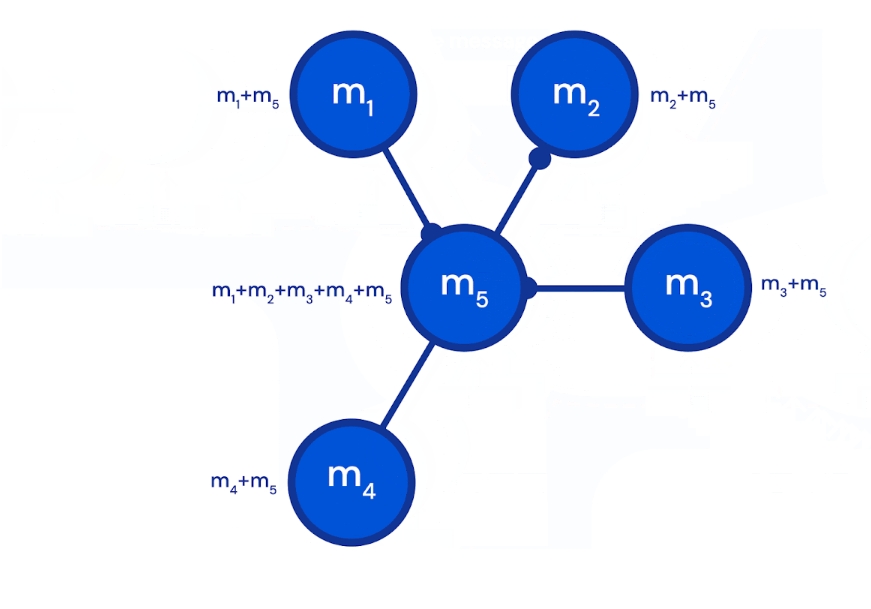
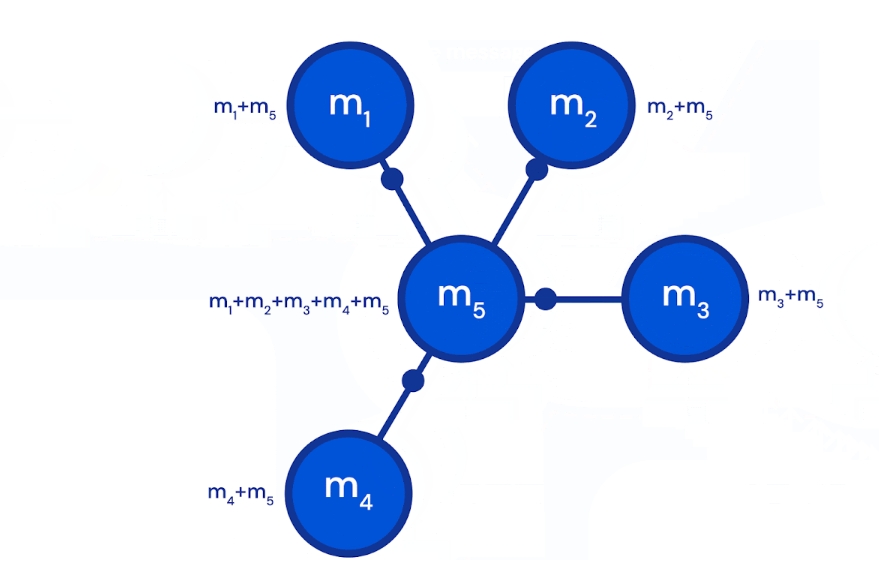
将道路分段,每个段是一个节点,段与段之间的关系为边
每个节点上有流量数据
预测未来几小时的流量
药物发现
药物的成本低,研发成本高,
GNN可以降低研发的成本
- 分子结构 -- 功能 ... 学习中
- 需要的功能 -- 分子的结构 预测
|
图表示学习
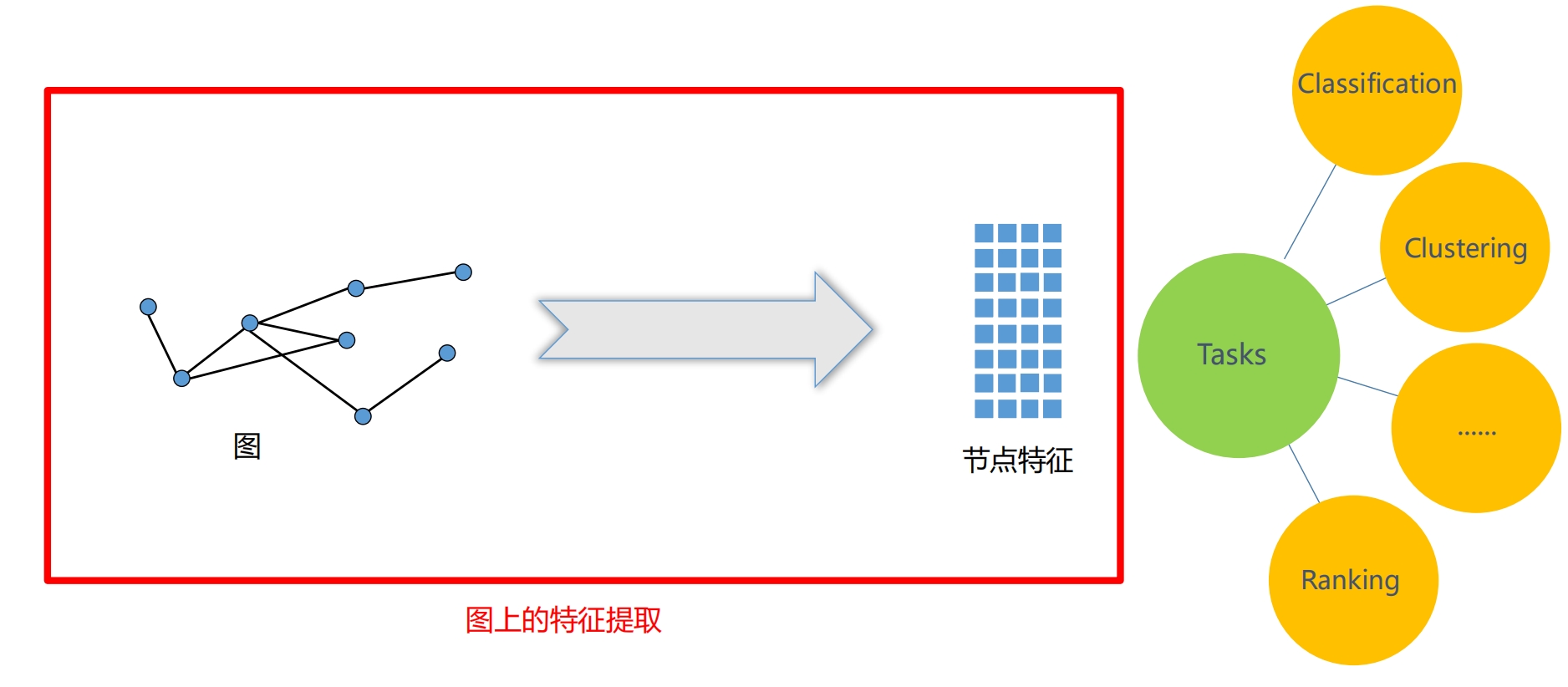
从图上提取特征,得到行列二维表,就可以转机器学习了 特征工程 - 手工提取节点信息 - 度 - 中心性 缺陷 - 手工麻烦 - 特征固定后,后续固定继承,无法最优 |
|
特征学习 改手工提取 为 自动学习 针对下游任务 从100个结构/节点特征选择10个,降维,灵活 表示学习 特征学习是选择,不改变 表示学习是从原特征中 学习出一组特征 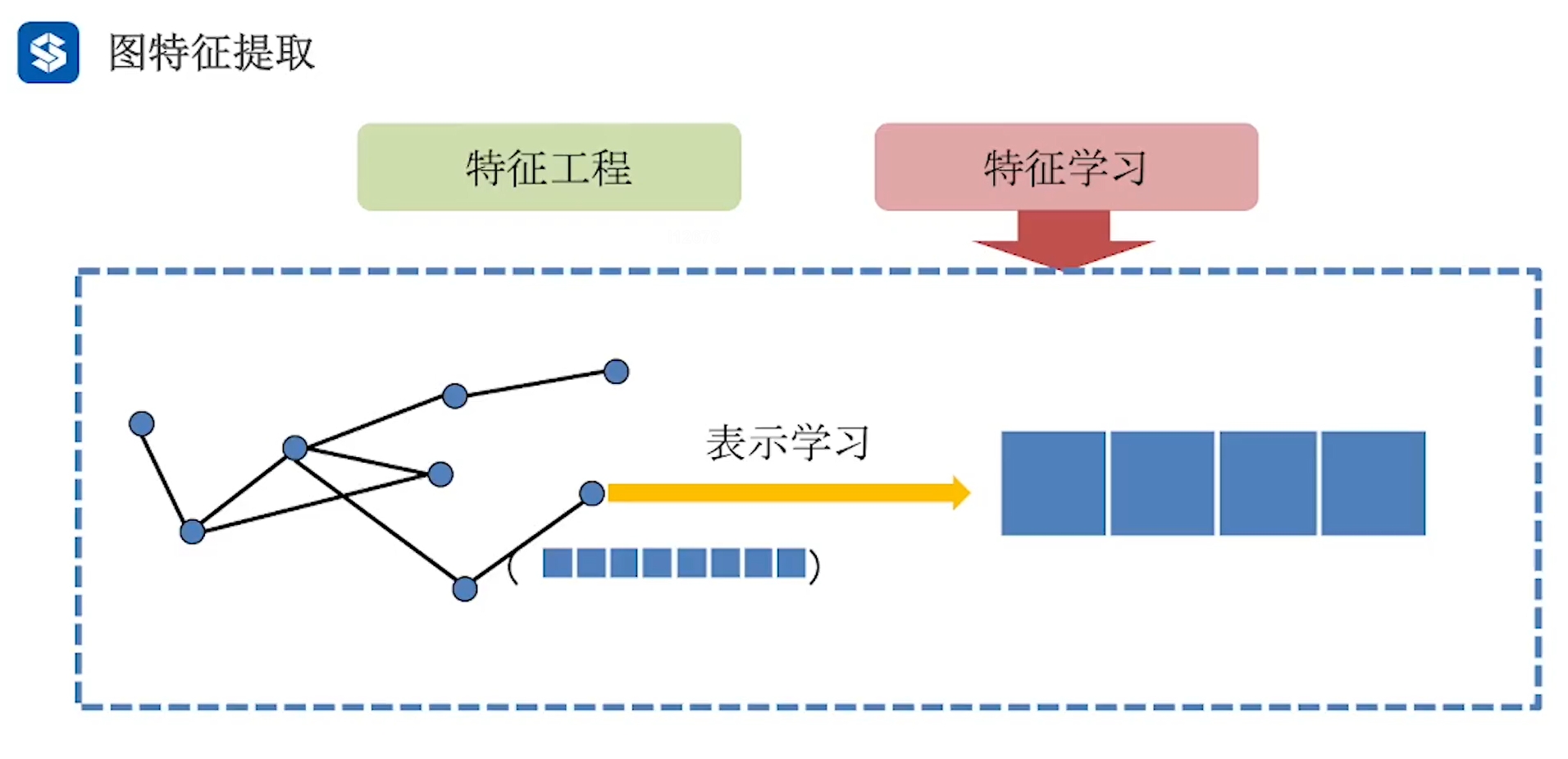
|
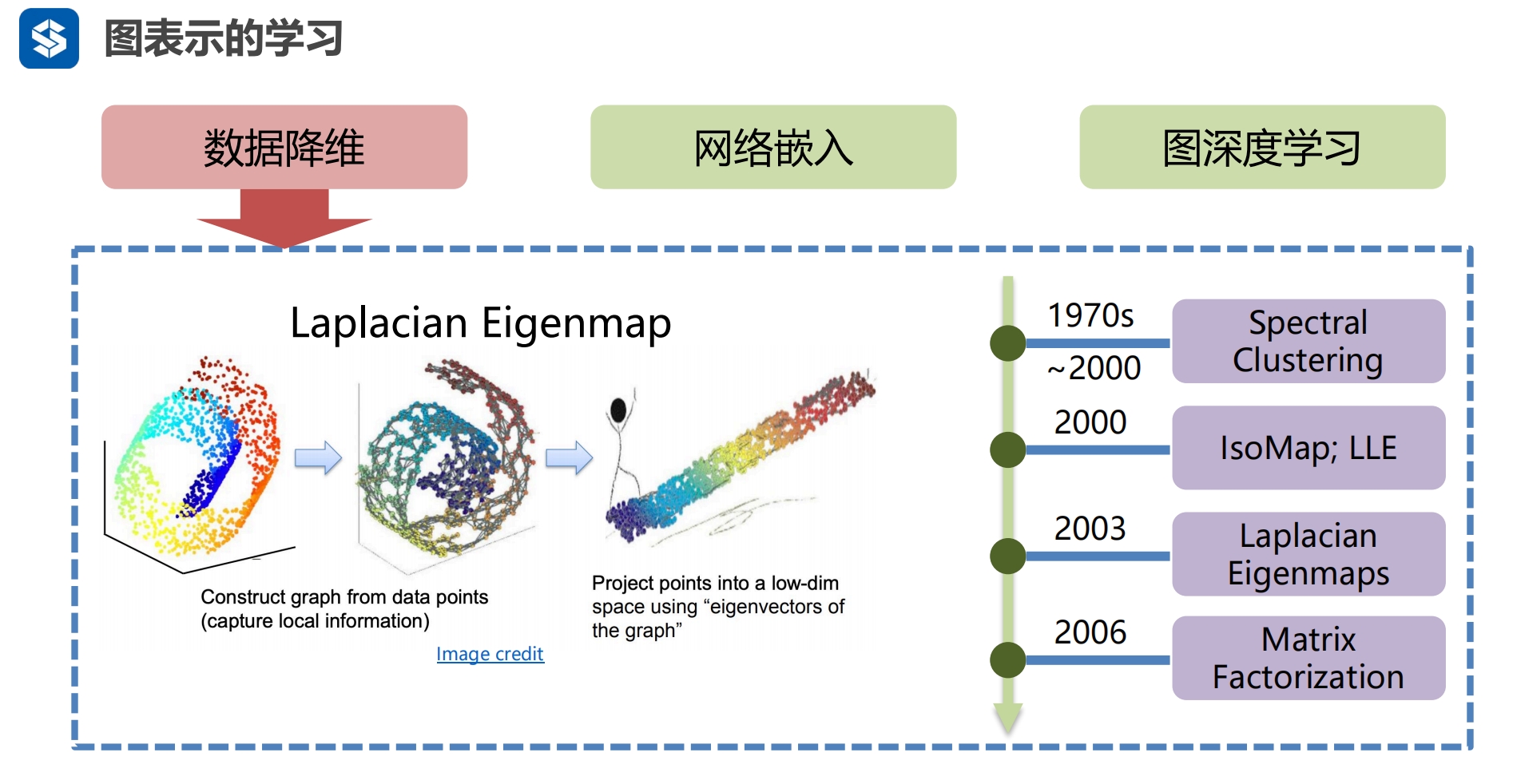
第1代 最开始1970-2000通过聚类的方式...降维 2006通过矩阵因子分解的形式降维 - SVD 奇异值分解 第2代 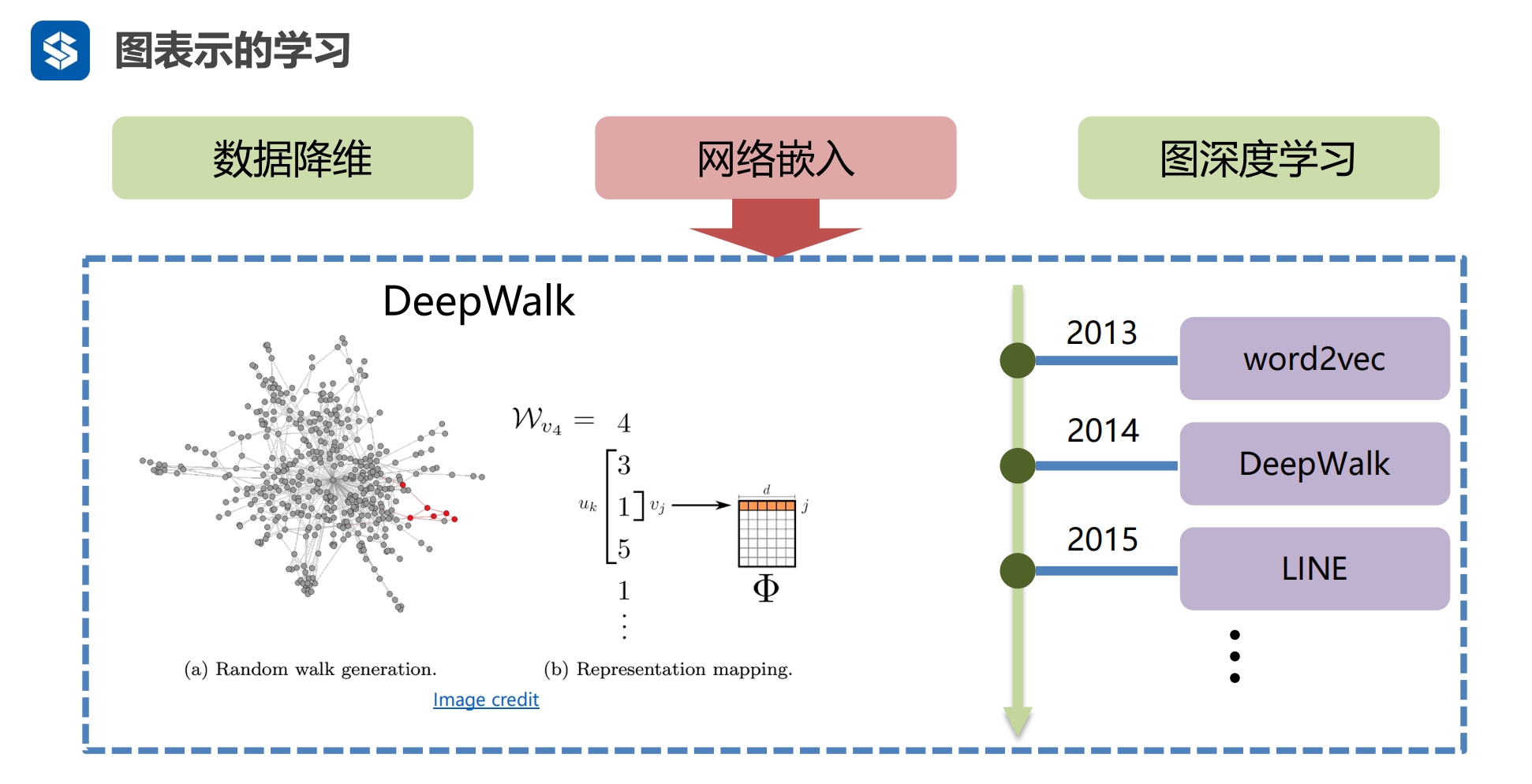
实际上也是矩阵分解 第3代:引入深度学习 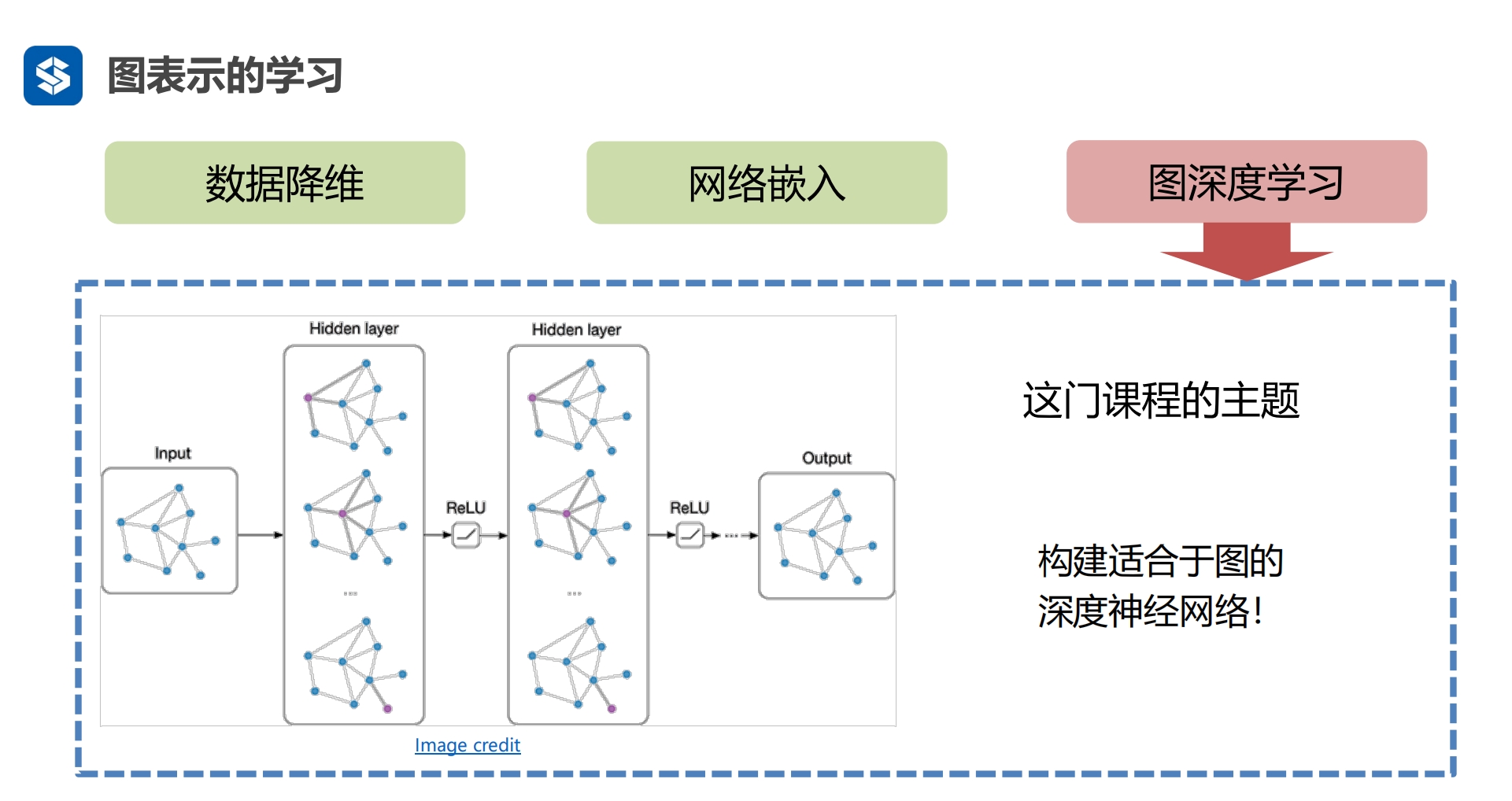
|
|
|
|
|
图论基础
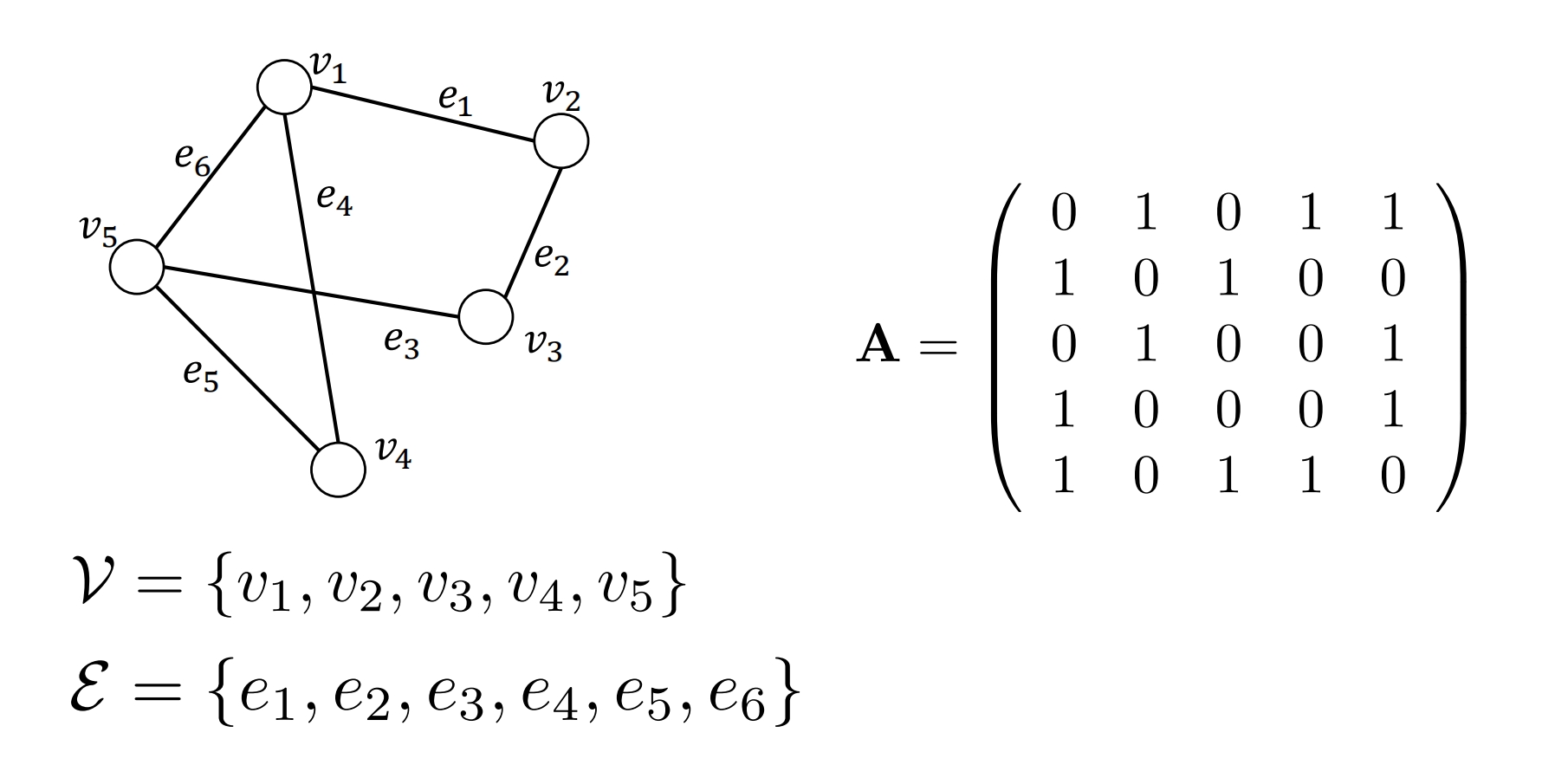
v:节点
e:边,无向,权重,有边为1,无边为0
矩阵n*n ,A为邻接矩阵
- v1与v2有边为1,无边为0
- 有5个节点,为5*5矩阵
- 第1行/列为第1个节点到各个节点的边
- 第2行/列为第2个节点到各个节点的边
关于主对角线对称,即A与其转置矩阵一样
|
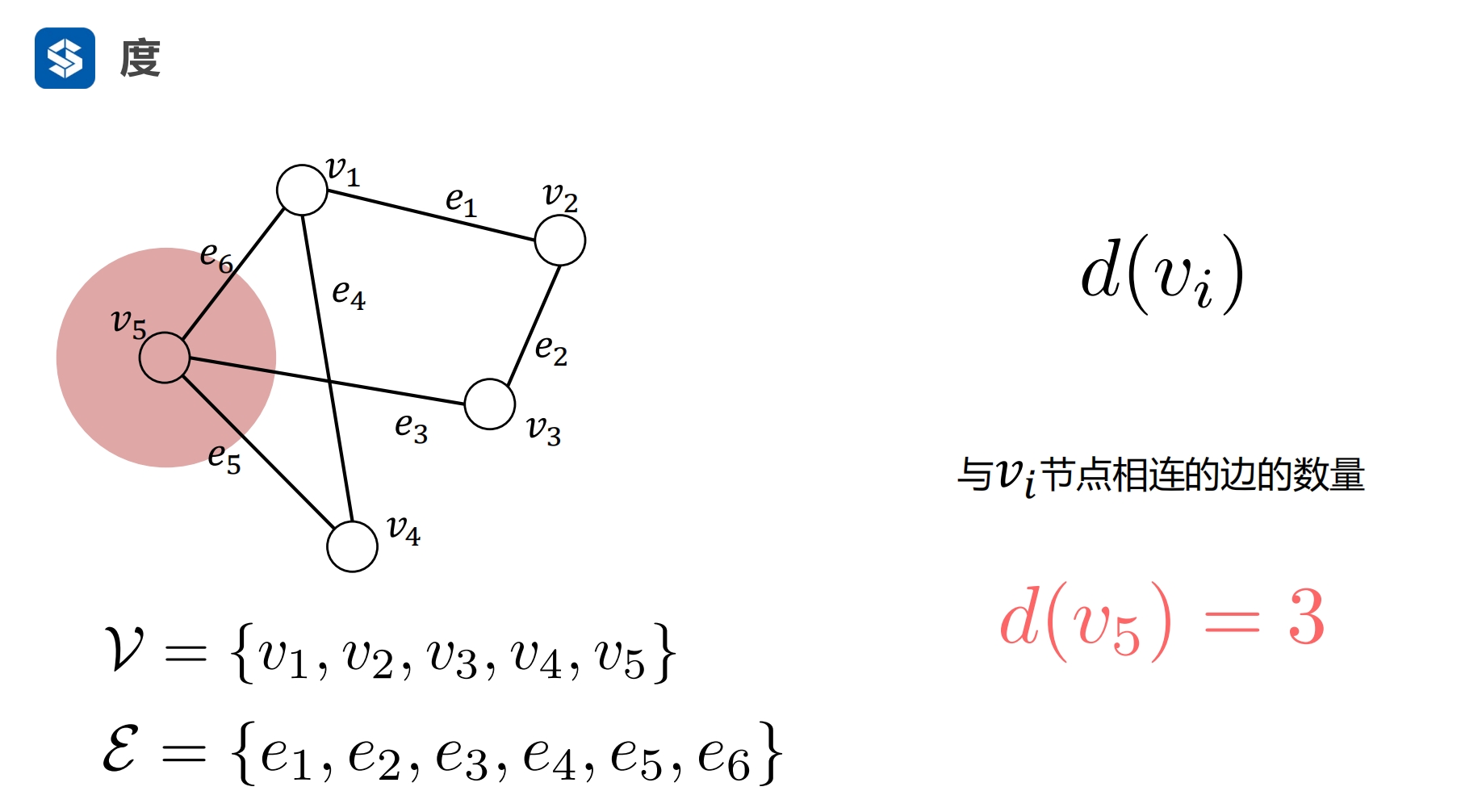
一个节点的度是该节点与其他节点之间边的个数
邻域:相邻节点的集合 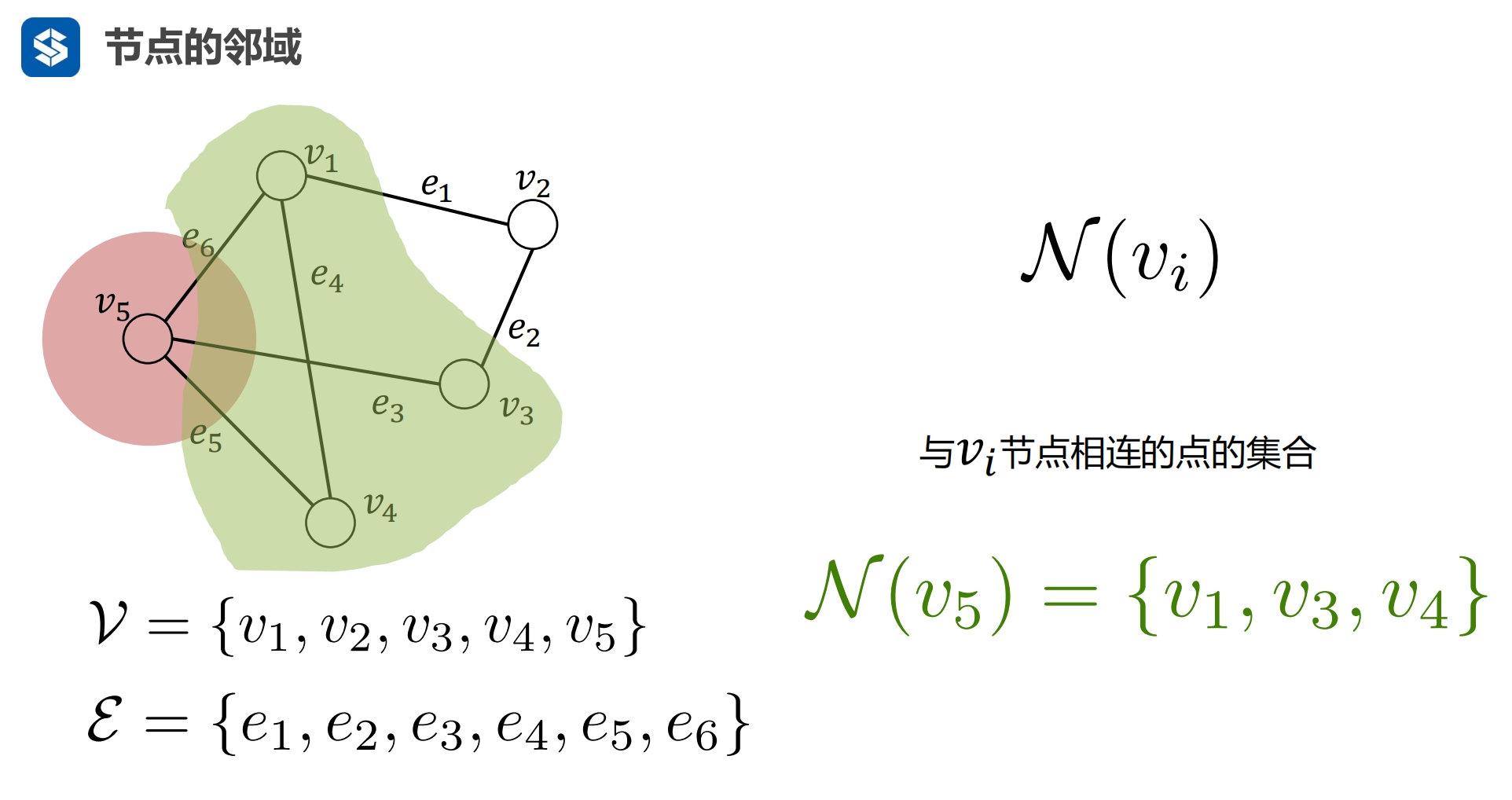
|
|
途径(walk): 两个节点之间的路径 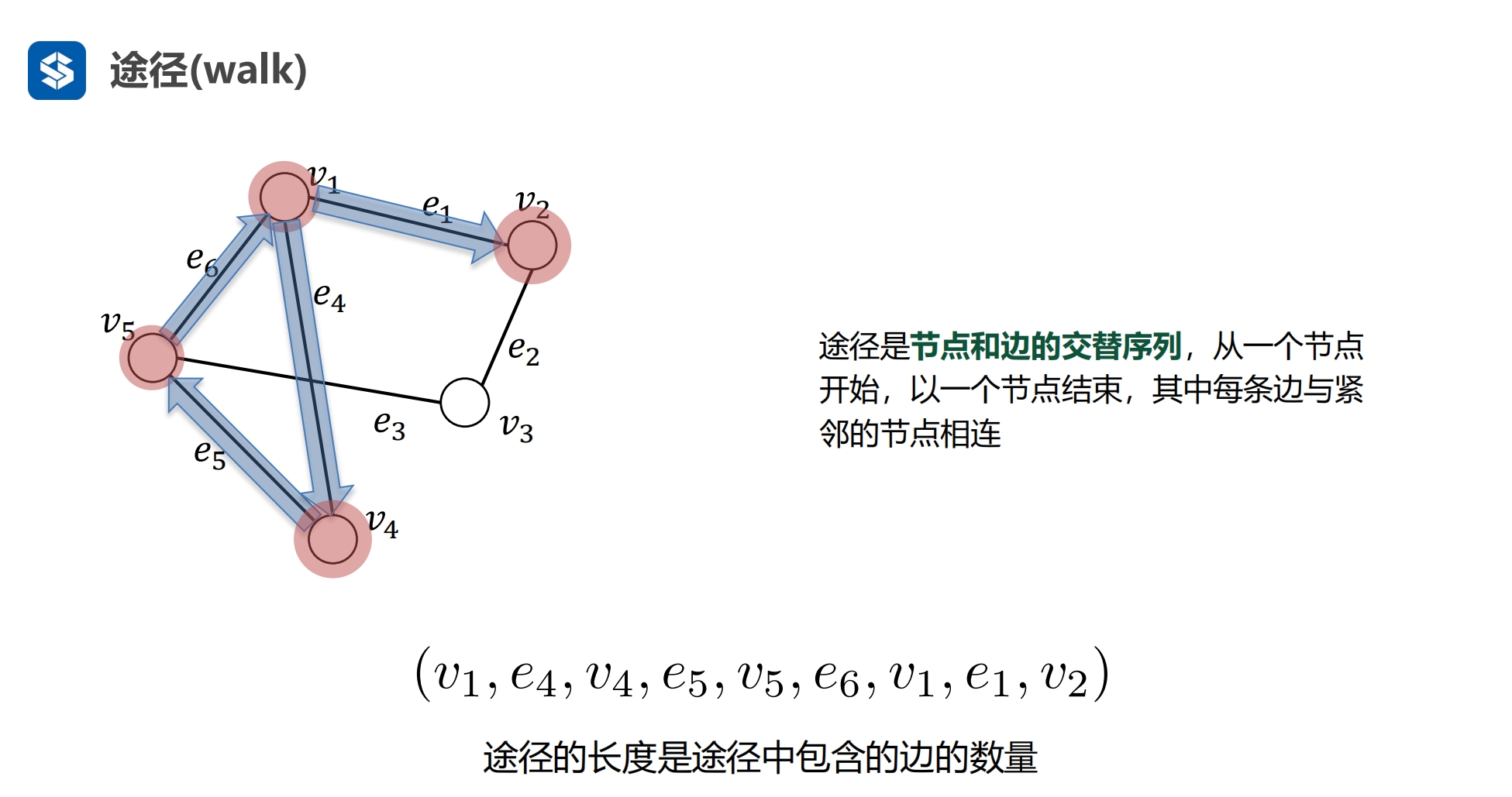
交替排列 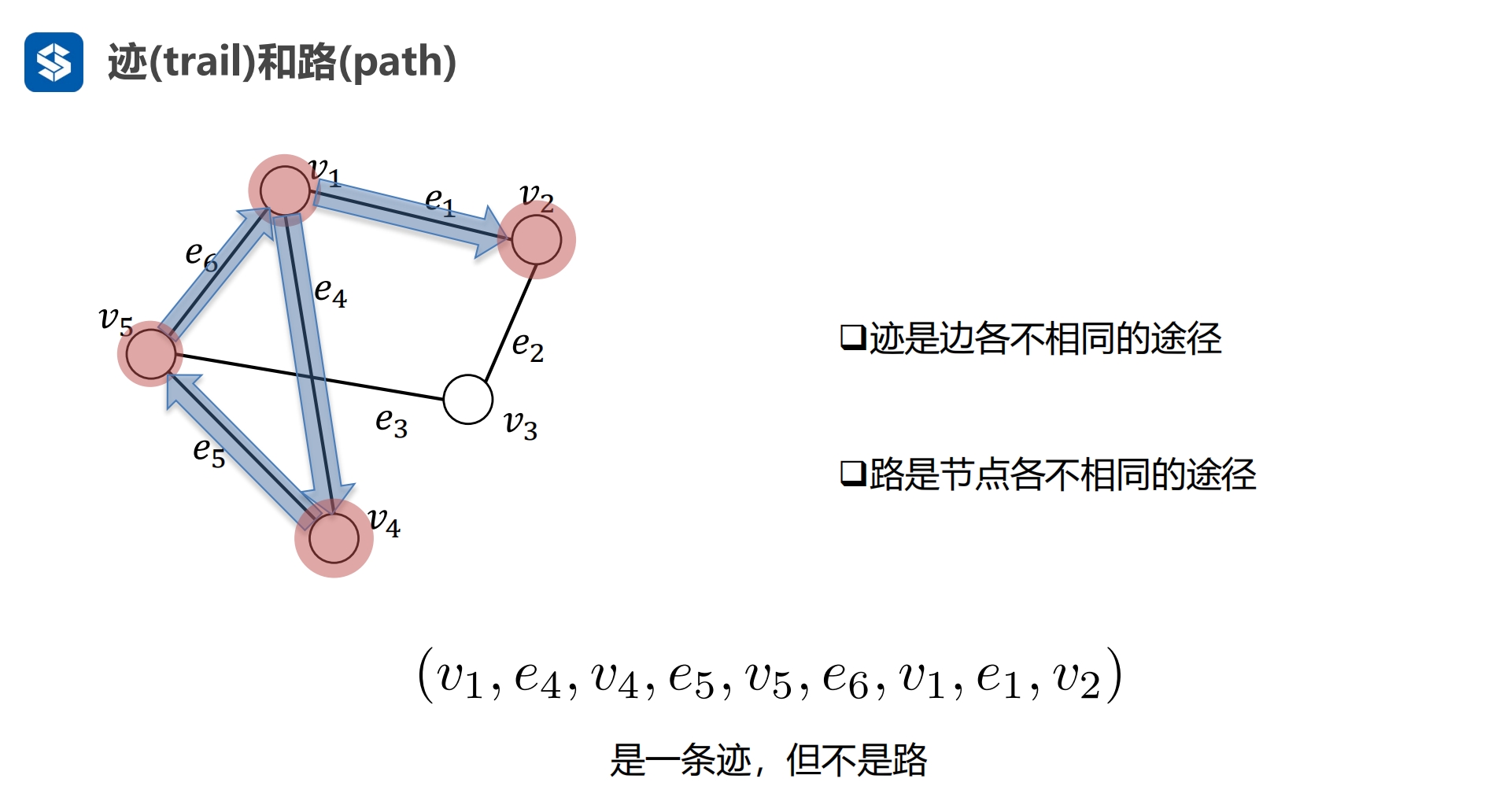
算法中并不严格区分 途径与路 |
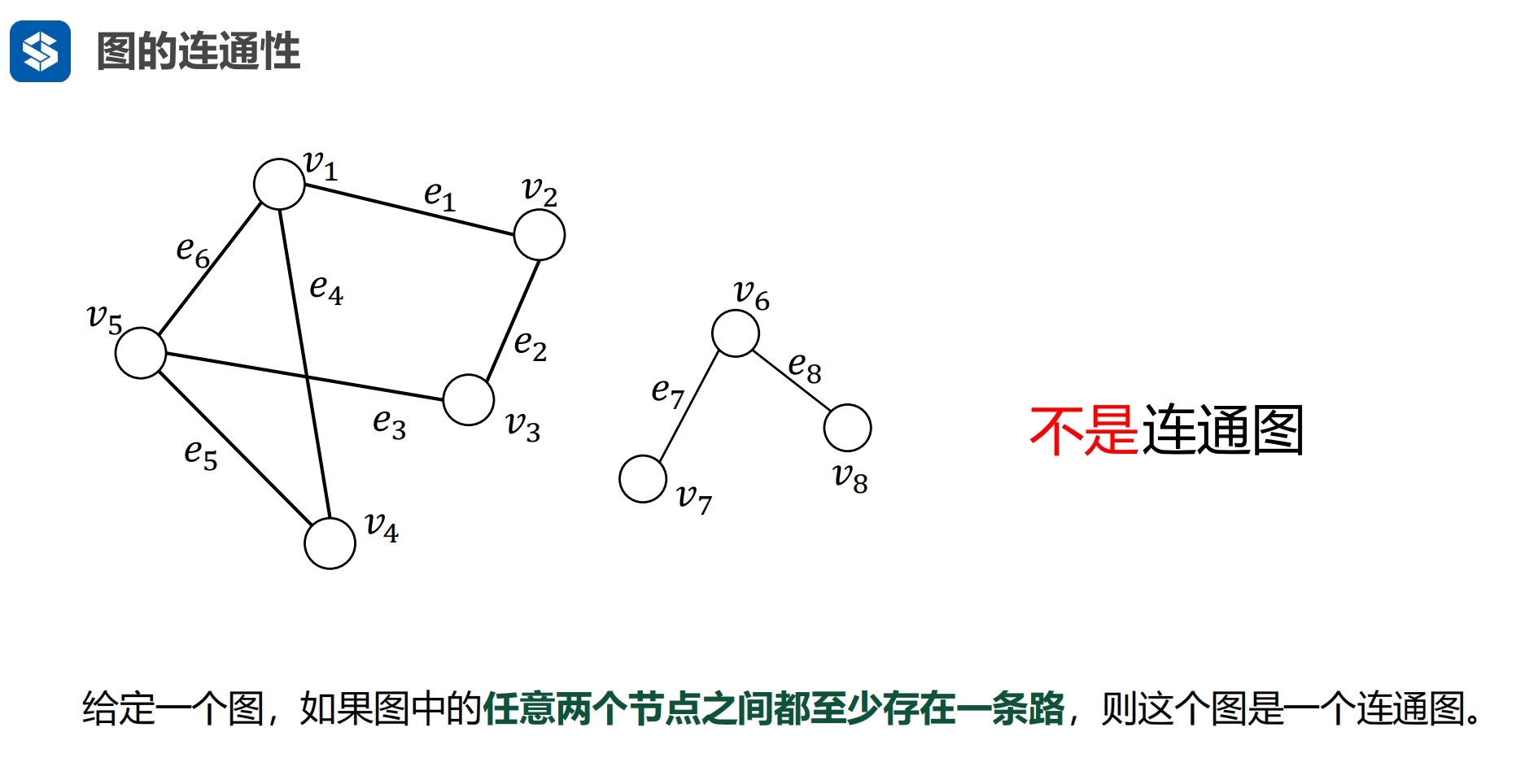
路的长度就是边的个数 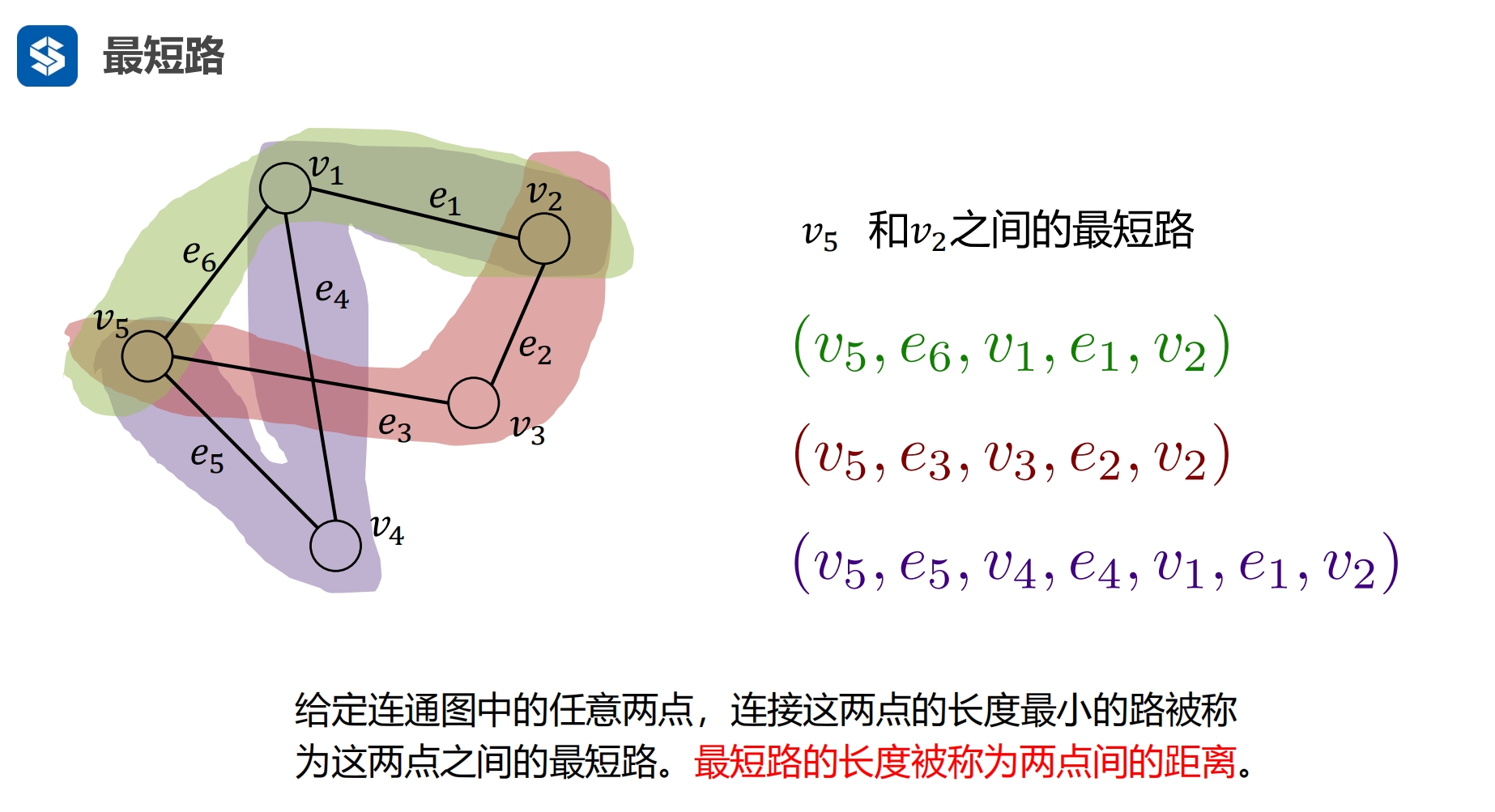
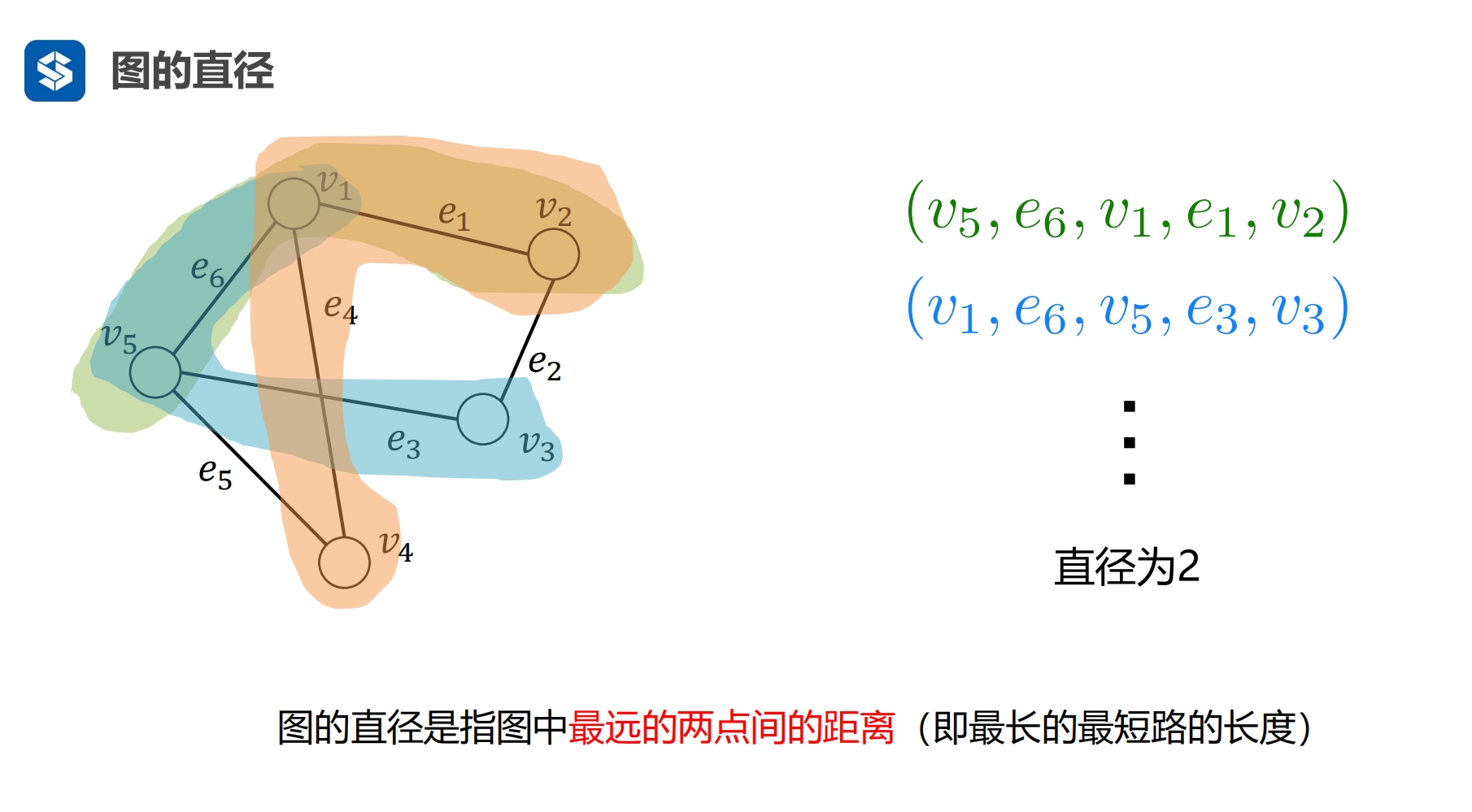
两个节点之间 最长的最短路径 |
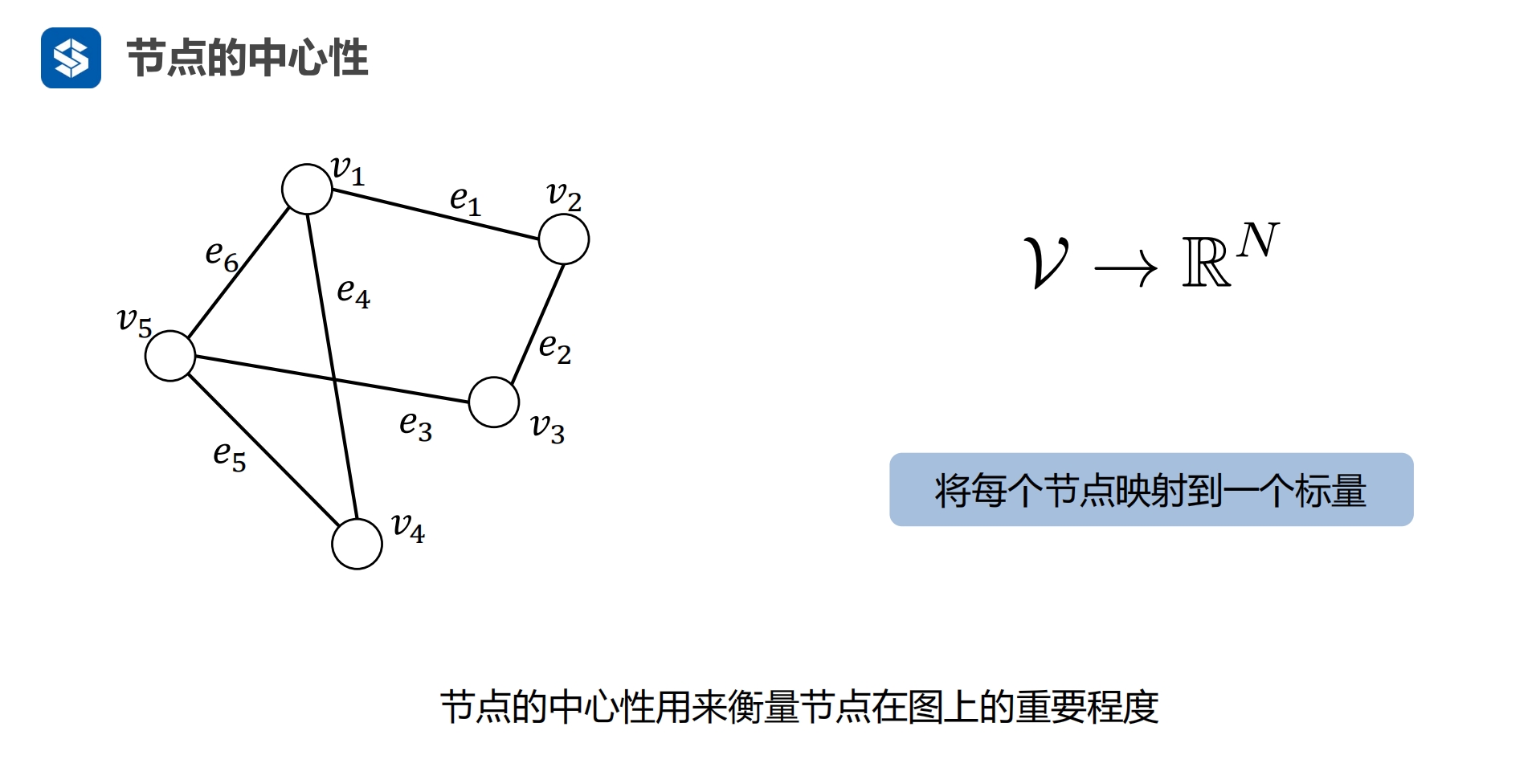
将节点转化为了一个数字,用数字的大小来代表重要性 度中心性:一行中边的个数 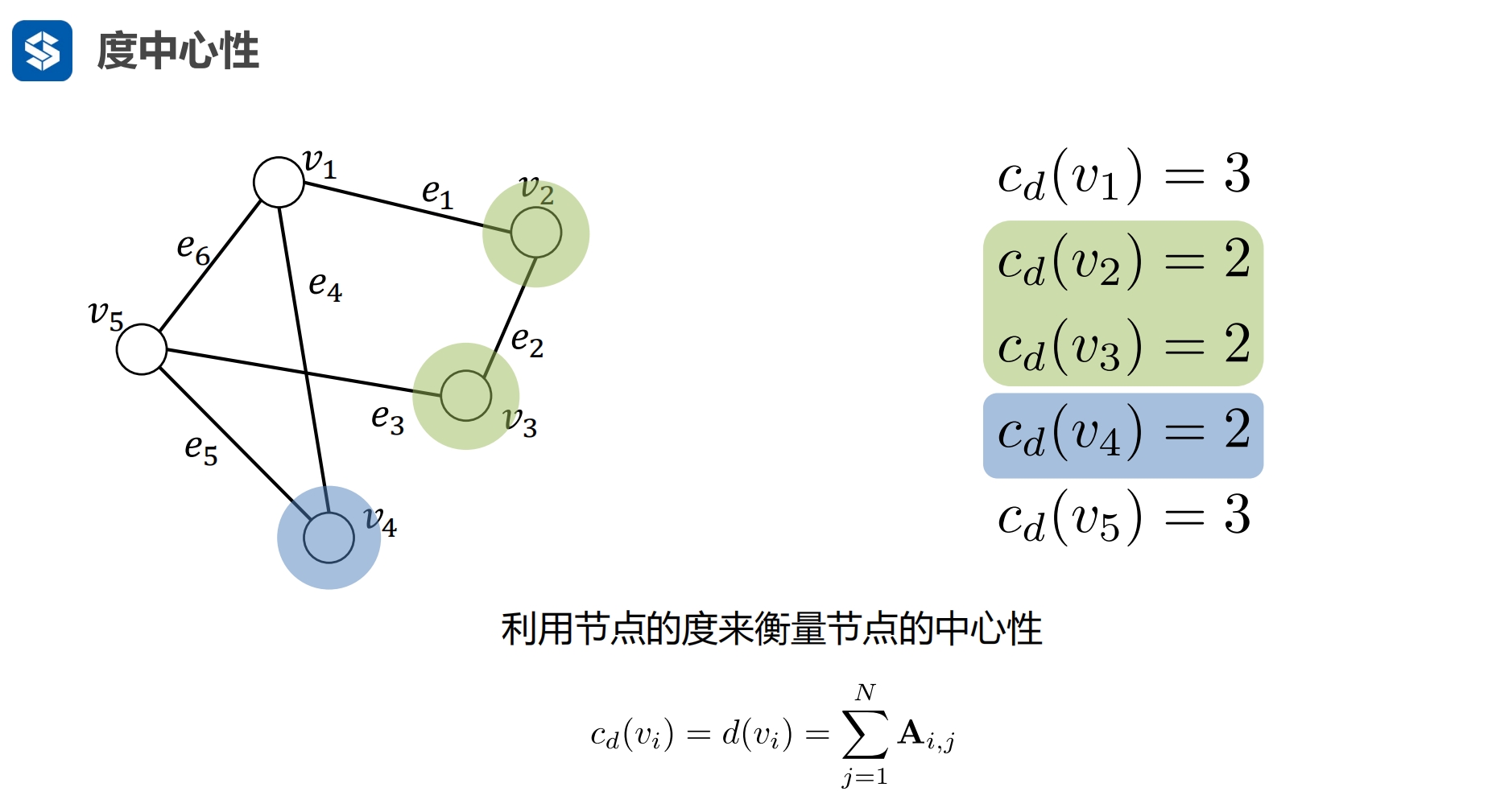
c 中心
d 节点的度
cd 节点度所表示的中心性
考虑两个因素
- 度:节点关联的边越多就表示重要性越高
- 自身:自身的信息
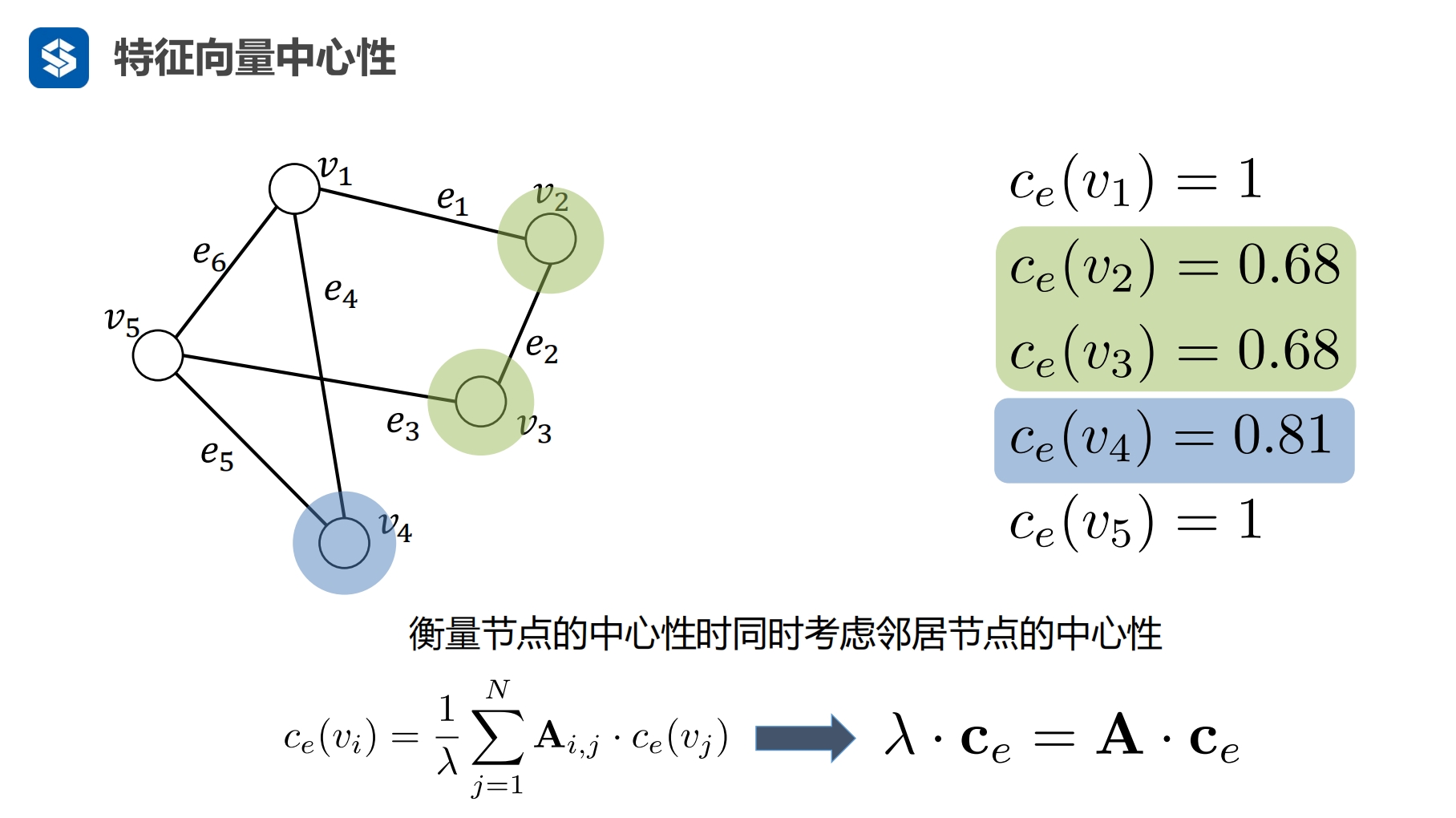
Ax = ax
a为特征值,x为特征向量,现在有关联矩阵A,就可以求出特征值a,以及对应的特征向量x
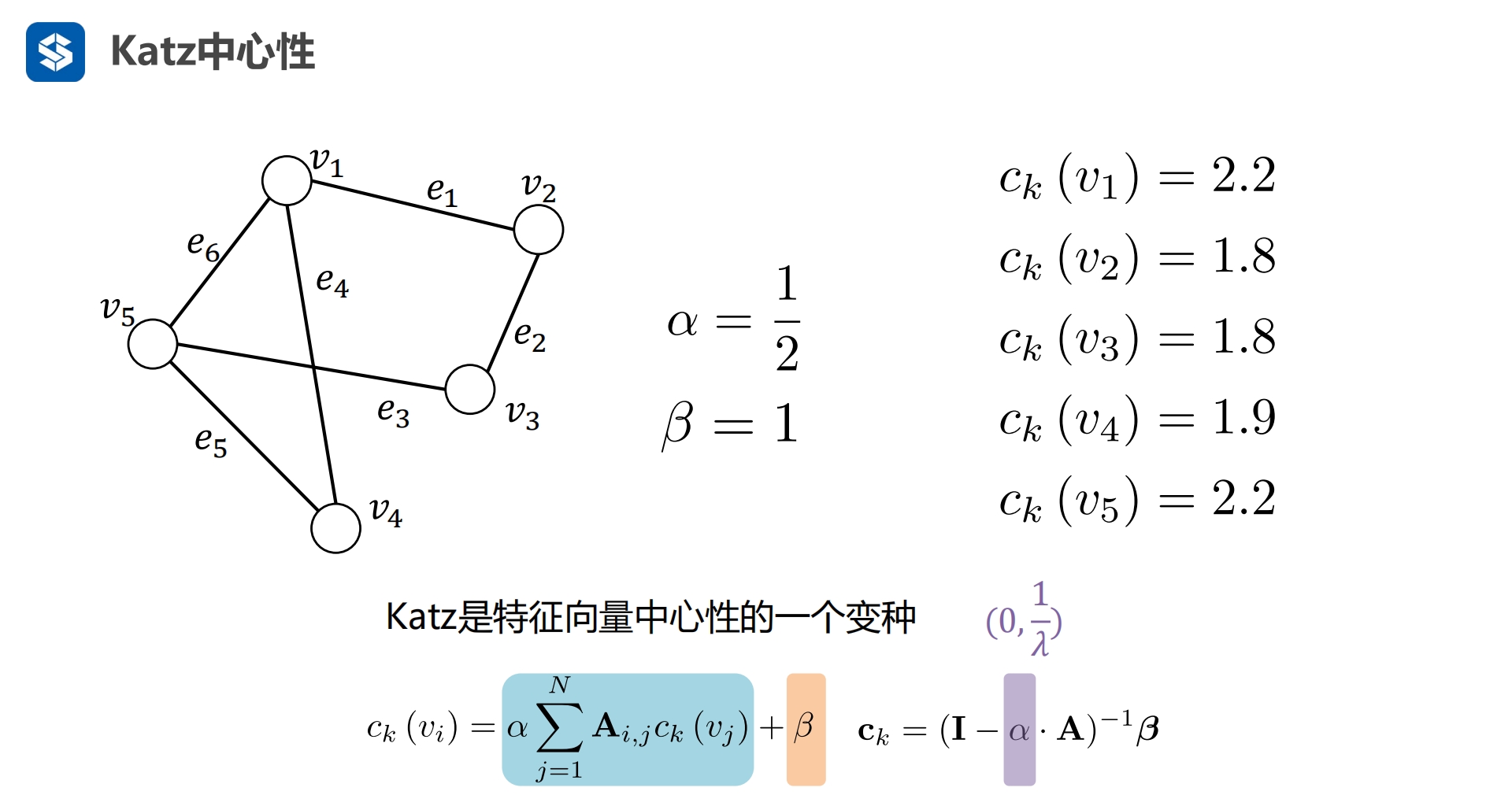
β实际为βi
节点关联的节点多
所关联的节点重要
自己重要 -- Katz中心性
|
图信号
|
一个节点代表一个信号 
RN是实数上的n维度向量,一个节点一个数值,n个节点形成一个n维向量
- n维列向量,一个节点映射到一个数值,
- n个节点映射到n个数值,形成n维列向量
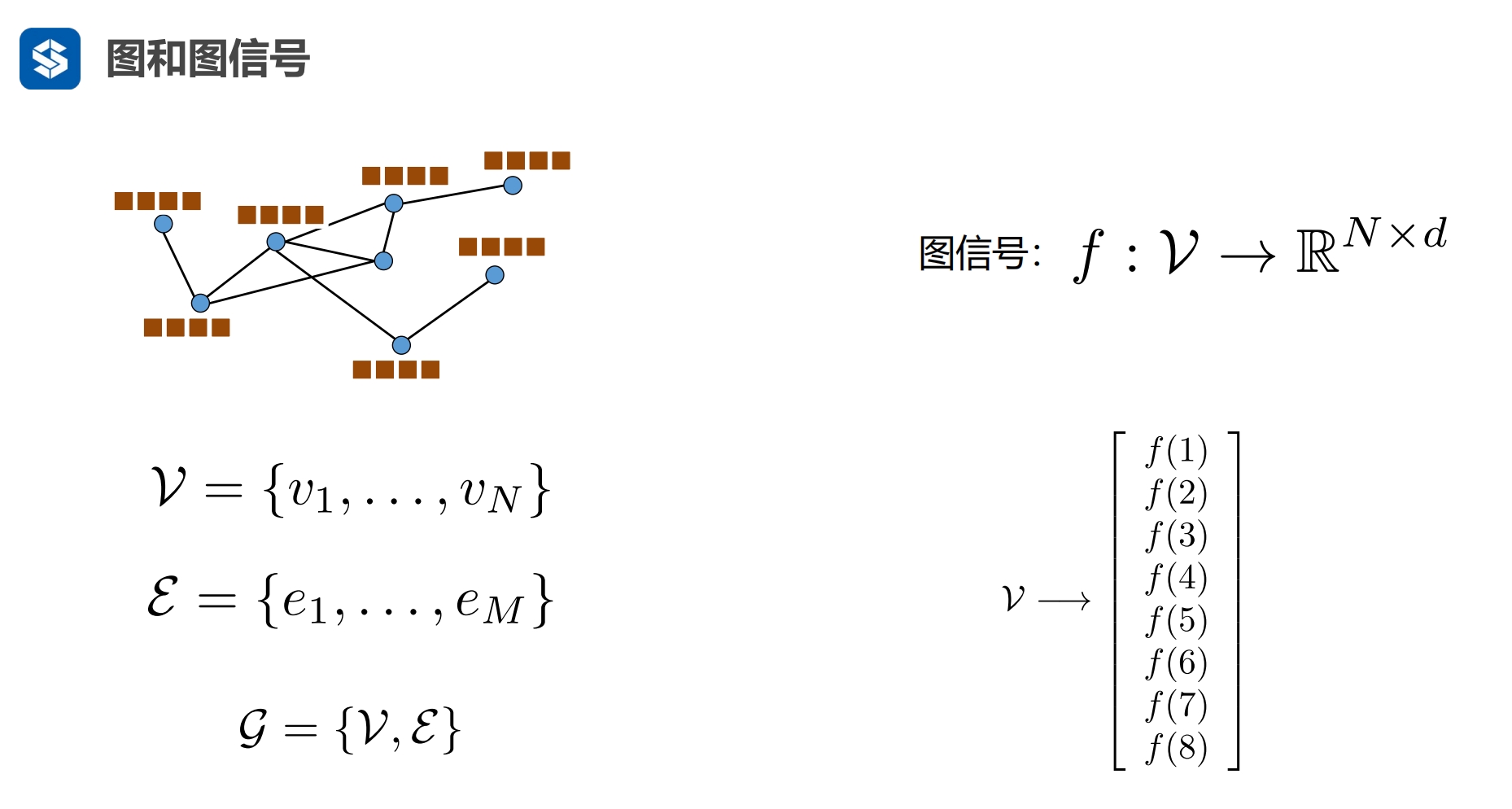
一个信号可以有多维,一维一个通道,图上表示的是4通道 - 如果是在机器学习中,说法就会换成一个对象的多个属性,只是叫法不一样 - 这里f(1)有4个数值
|
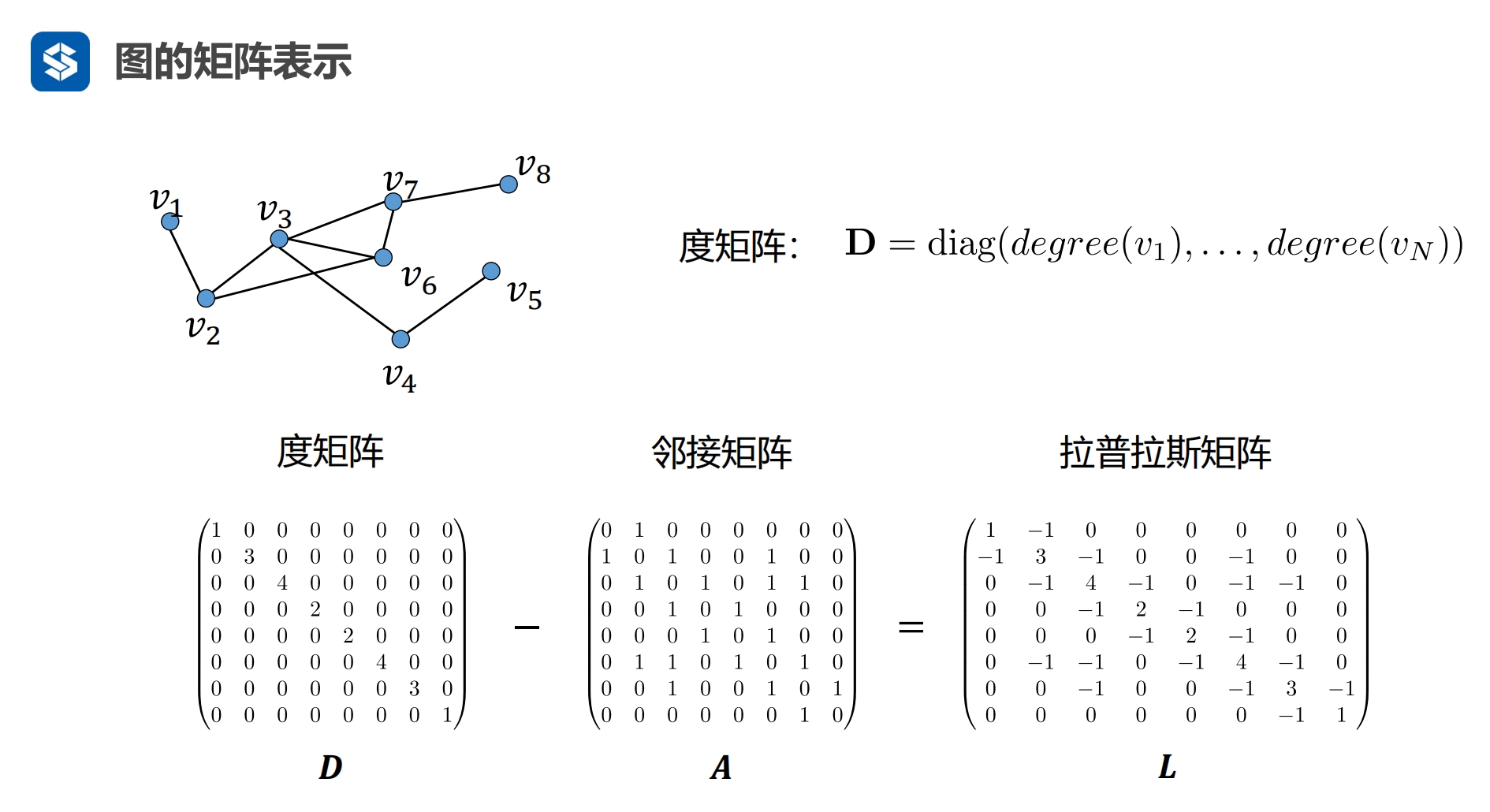
度矩阵为对角阵,用一个行/列向量表示节点的度,
- 第i个节点只在向量的第i个元素上有值,该值为该节点的度
- 其他位置上的元素皆为0
f,h为 列向量
vj 是vi的相邻节点
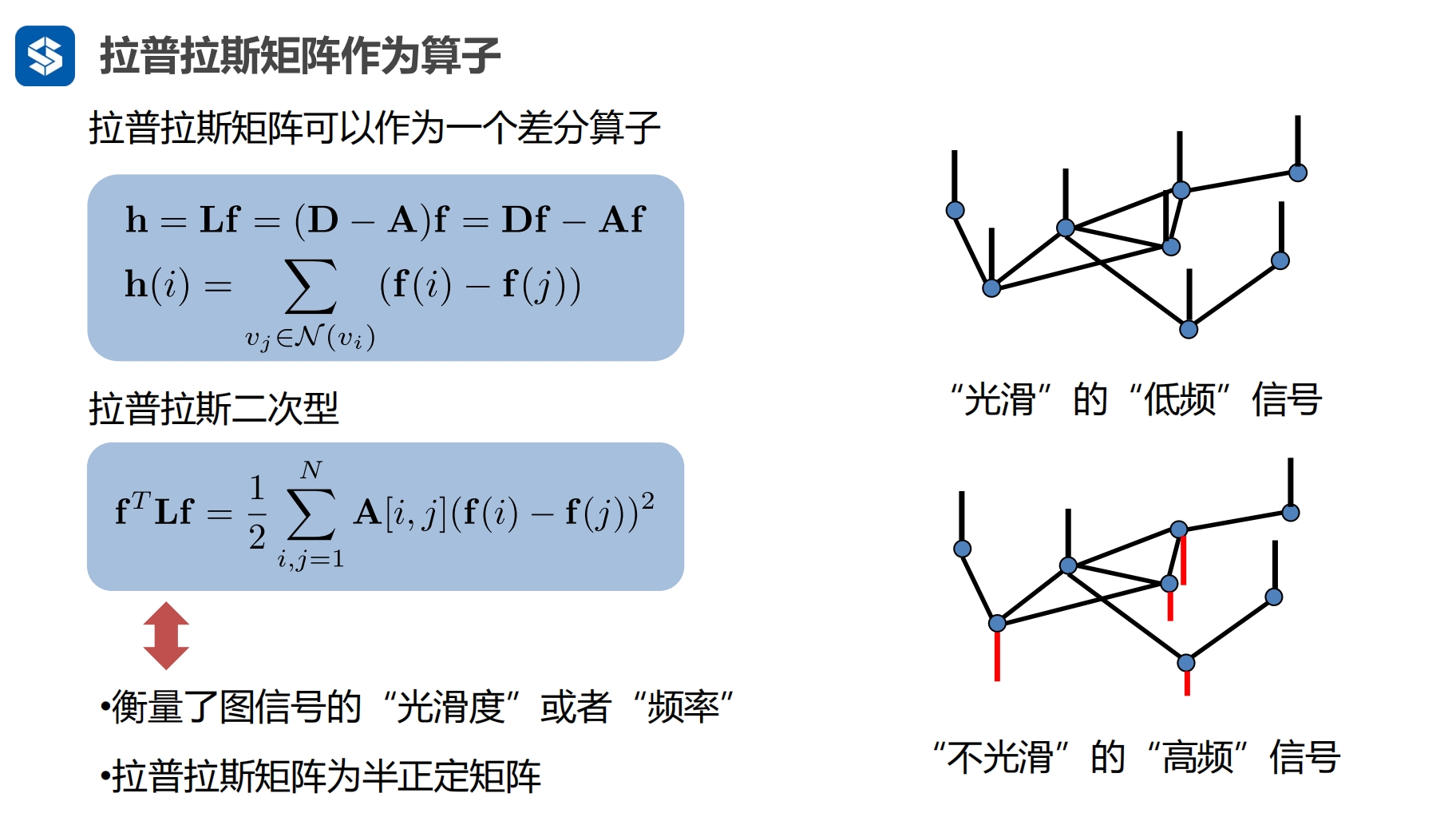
hi 是 第i个节点 与 其相邻节点 信息差的和
- 两个节点的信息值想减后有正有负,再相加后会 中和
- 因此对差做平方
如果两个节点之间有连接的话
- 二次型可以衡量两个节点信息值的差异
- 如果节点之间相近,则过渡平滑...
|
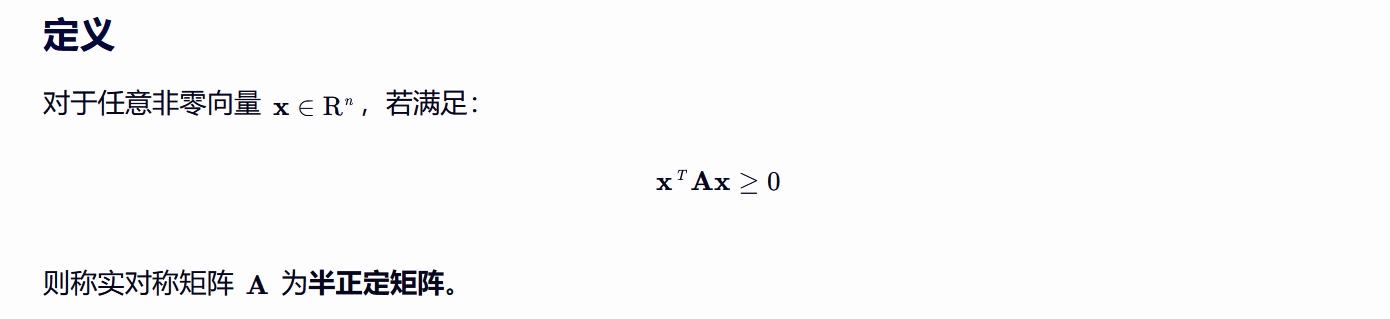


|

半正交矩阵可以进行特征分解
邻接矩阵的对角线为为0
- 可能因为这个的原因,它会有一个为0的特征值
- 从而导致它为半正定矩阵
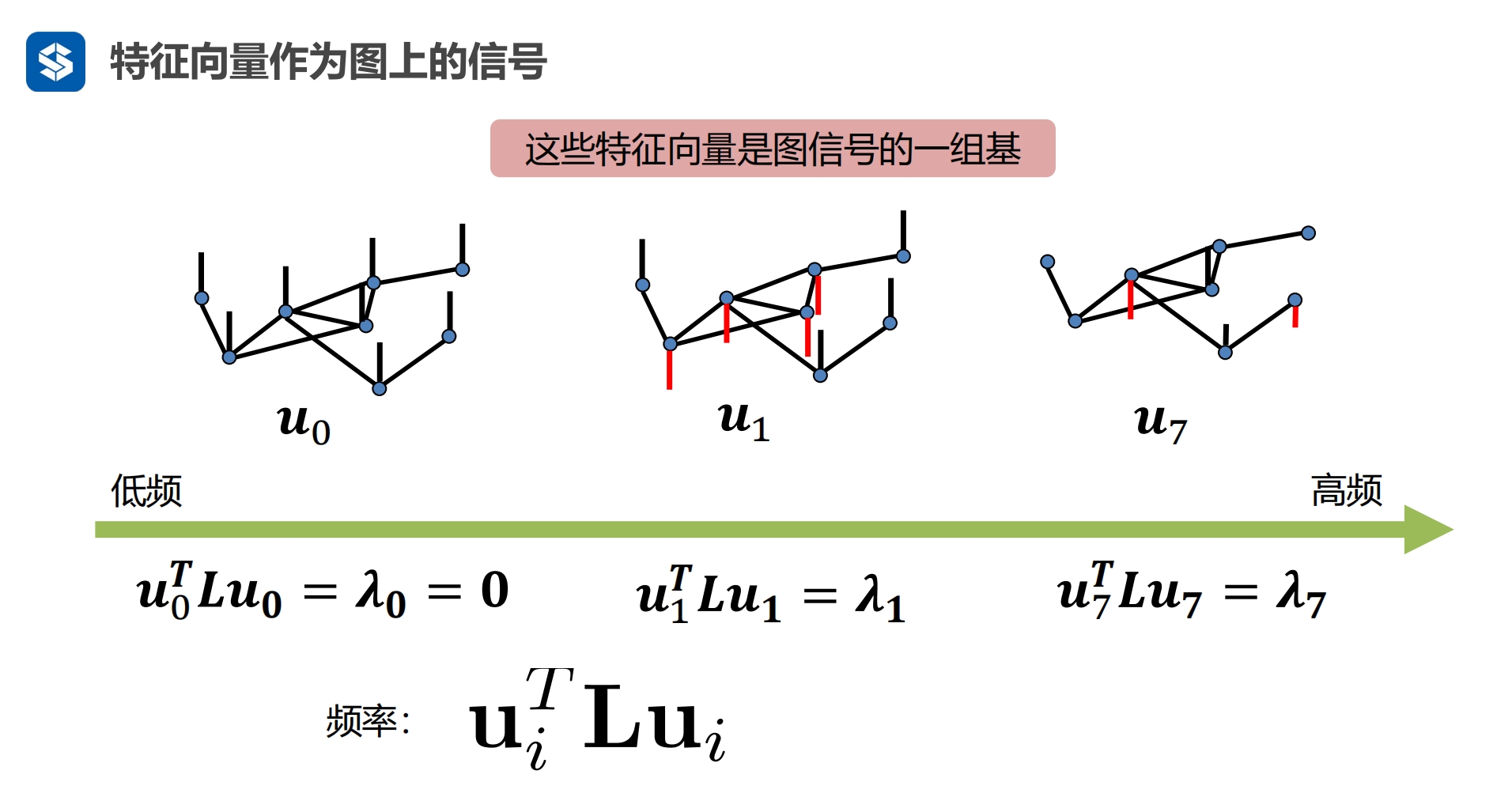
u是特征向量,应该还是一个单位向量,其模为1,这样最后才能剩下一下特征值
将该特征值作为信号的频率,由小到大排列,就是频率由低频到高频排列
|
|
|
图傅立叶变换
|
向量与线性组合 任何一个图信号都可以表示为一组特征(或者叫特征向量)与一组特征向量的线性组合 特征值1*特征向量1 + 特征值2*特征向量2 ... 特征值n*特征向量n 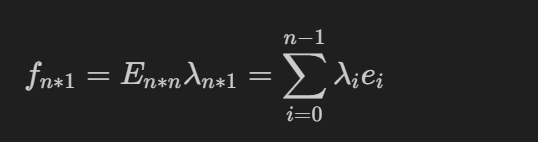
特征向量与特征值 
SVD 奇异值分解(Singular Value Decomposition, SVD)是线性代数中的一种分解方法, 它可以将一个矩阵分解为三个特殊矩阵的乘积。 SVD 在信号处理、统计学、机器学习等多个领域有着广泛的应用, 尤其是在数据压缩、去噪和特征提取等方面。 
然而,在实际编程中,尤其是在使用 NumPy 库进行 SVD 分解时, 返回的 Σ 矩阵通常以向量形式给出,而不是完整的对角矩阵。 因此,如果你使用 U, S, V = np.linalg.svd(A) 进行 SVD 分解,得到的各部分含义如下: 
使用这种方式,你可以通过 np.diag(S) 将 S 转换为一个对角矩阵,然后手动构造出原始的 SVD 形式: 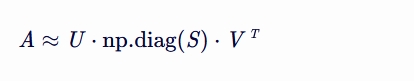
注意,这里的“≈”表示当 A 不是方阵或者其秩小于其行数和列数的最小值时, SVD 分解后的重构可能只是原矩阵的一个近似。 如果 A 是方阵且满秩,那么这种分解是精确的。
|
U,S,V = np.linalg.svd(A) U与V皆是正交矩阵 方阵中对称阵比较特殊,以对称阵举例说明SVD import numpy as np A = np.array([[3, 5, 7], [5, 1, 0],[7,0,3]]) U,S,V = np.linalg.svd(A) U.shape,S.shape,V.shape ((3, 3), (3,), (3, 3)) 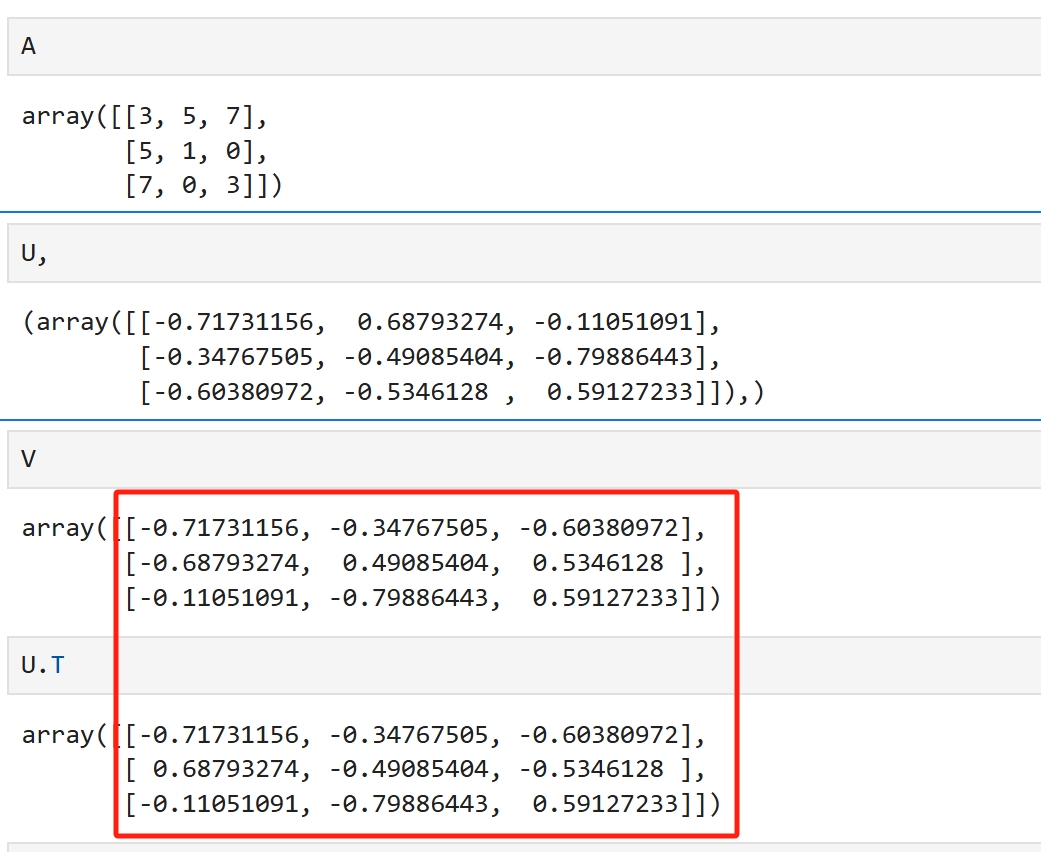
当A为对称阵时,U的转置就是V,由于U是正交矩阵,U的转置就是U的逆,于是此时的SVD就是 V的逆矩阵,S,V = np.linalg.avd(A) 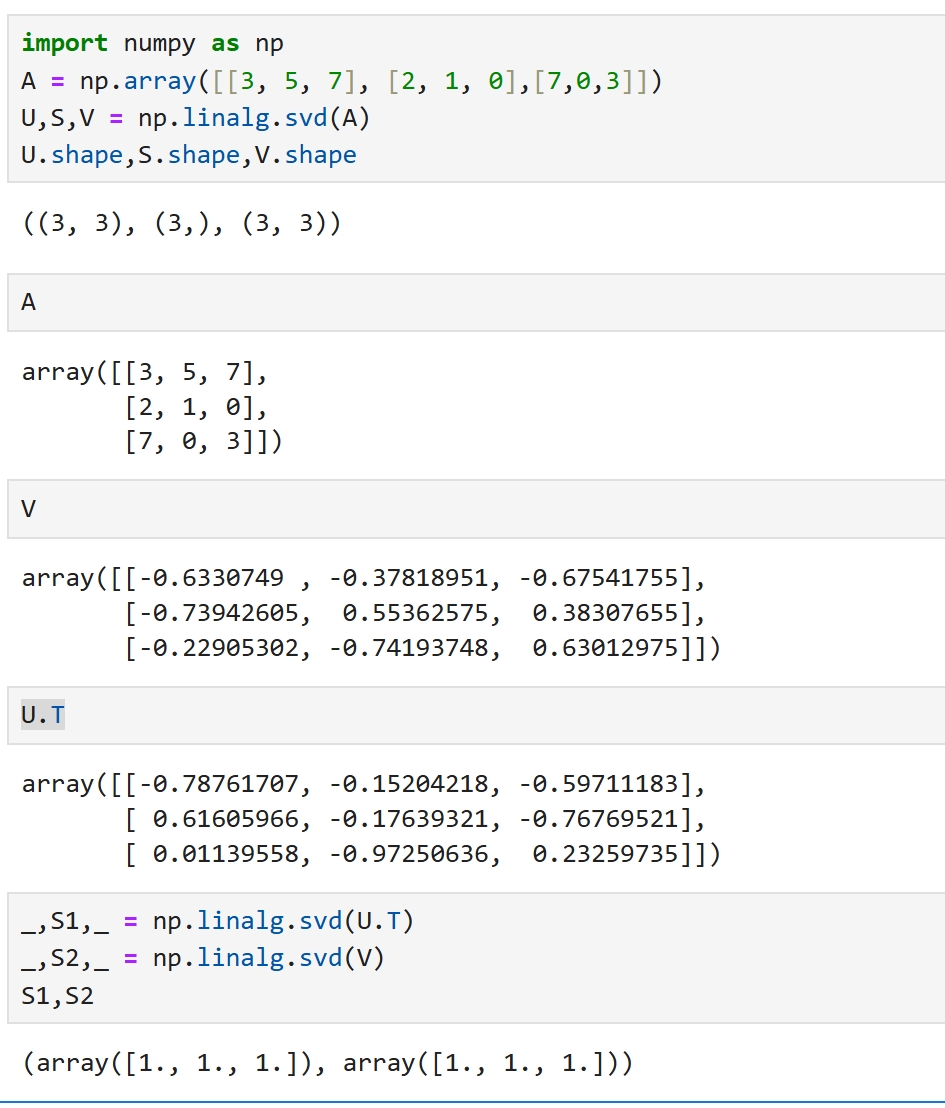
当A不为对称阵时,U与V不再满足这种关系,但它们依然是正交矩阵, 其特征值都是1,其结构依然是比较相似的 V[:,1]@V[:,2] -2.7755575615628914e-16 V[:,1]@V[:,0] 8.326672684688674e-17 V[:,2]@V[:,0] -5.551115123125783e-17
|
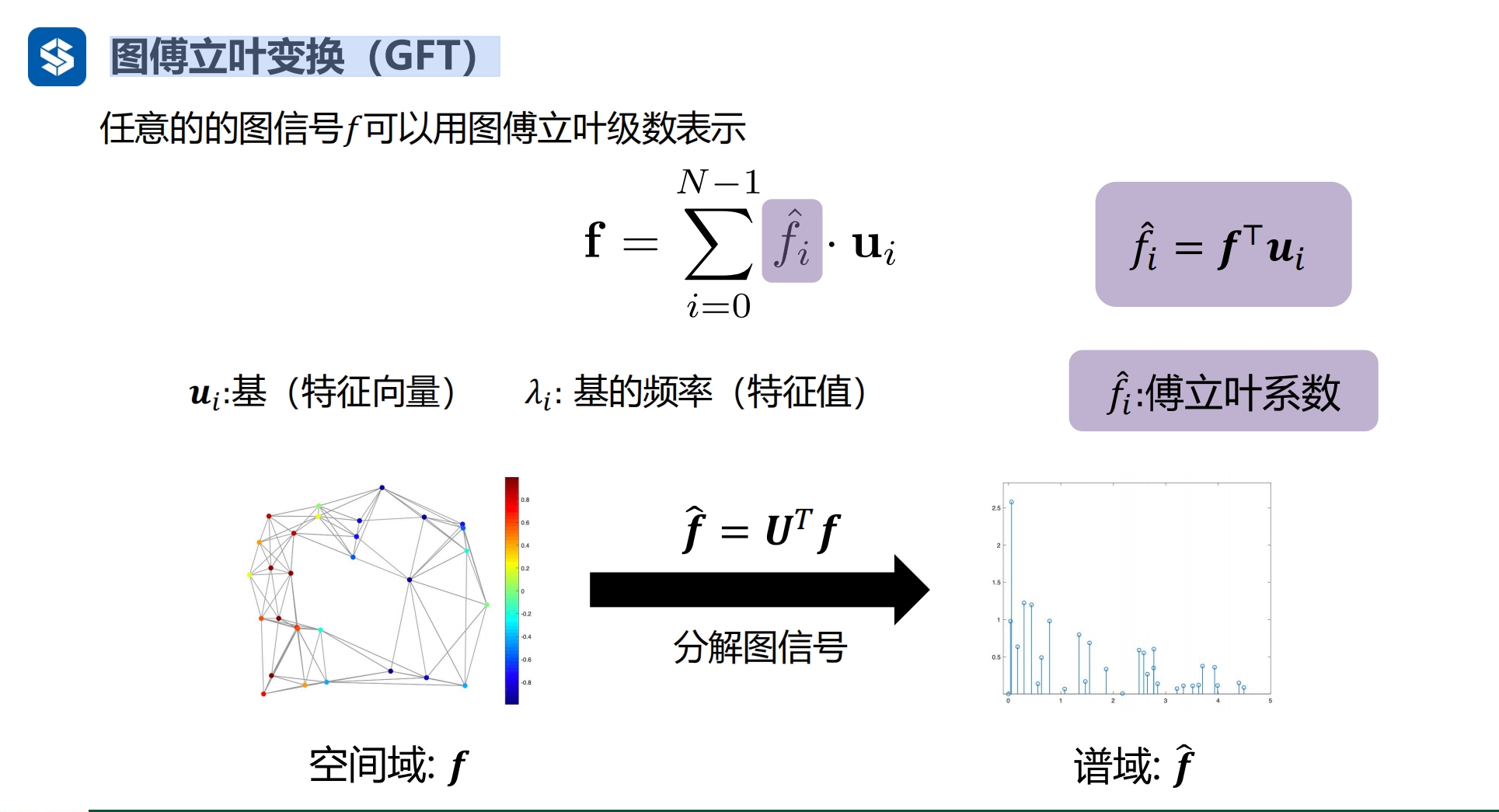
傅立叶变换
通过傅立叶级别将图信号从空间域变换到谱域
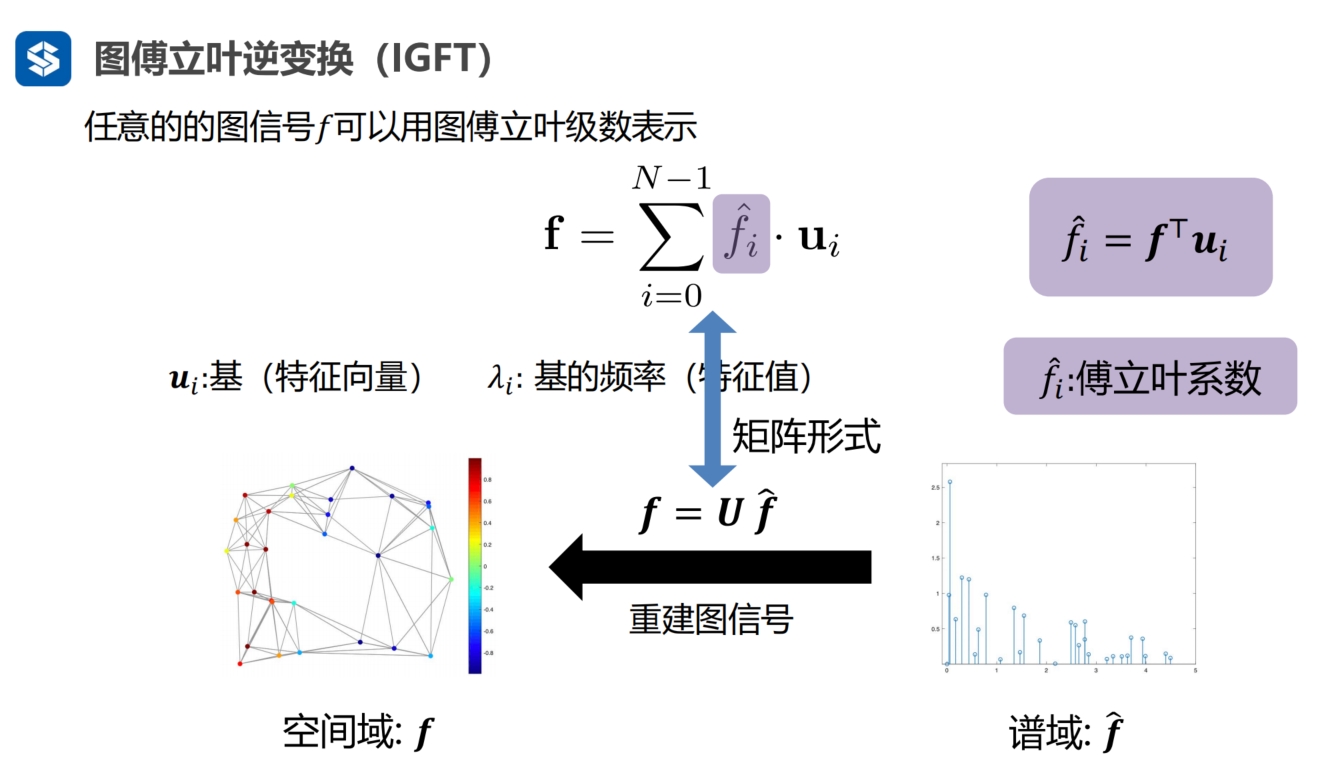
反傅立叶变换
U是正交矩阵,空间域到谱域的公式两个同时乘以U的转置矩阵后,就得到了谱域到空间域的变换公式
|
|
|
|
|
|
|
|
复杂图
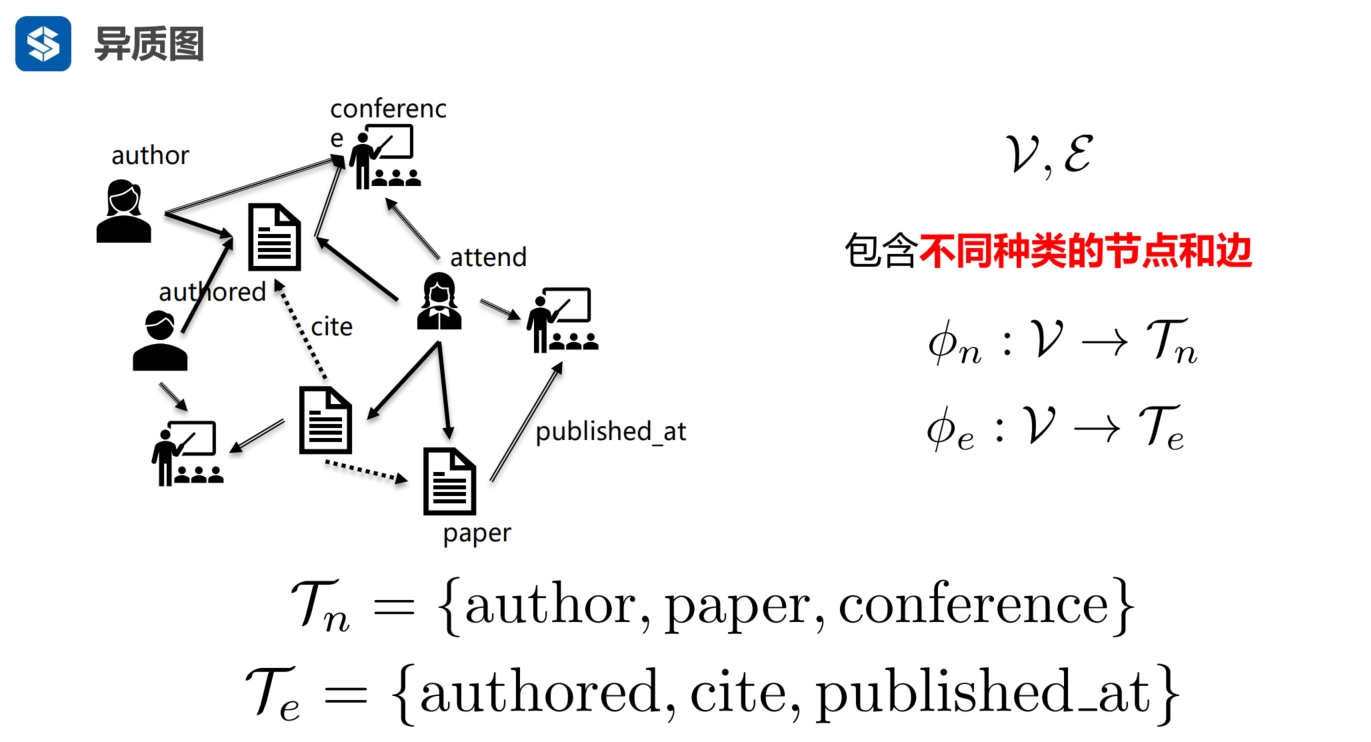
简单图:只有一种节点类型,边也只有一种边
|
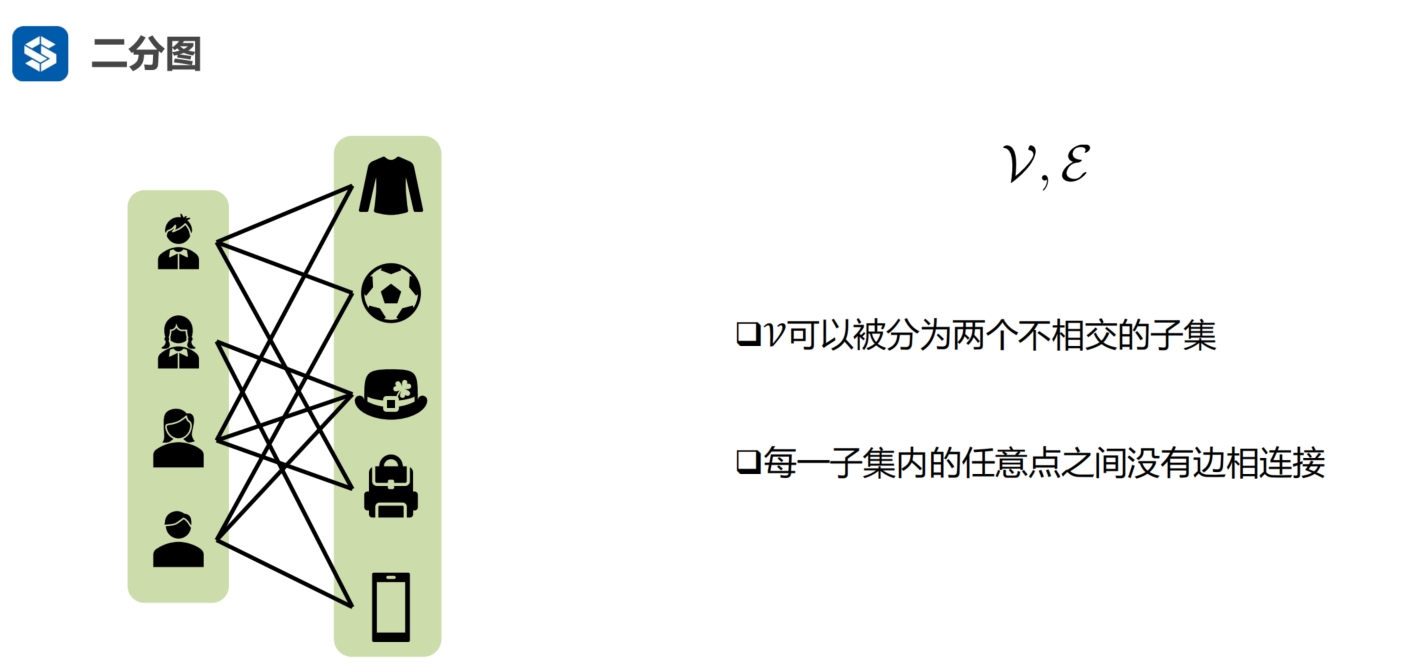
用户是一类节点
用户喜欢的事物是一类节点
用户与事物之间有边,用户与用户之间,事物与事物之间是没有边的
|
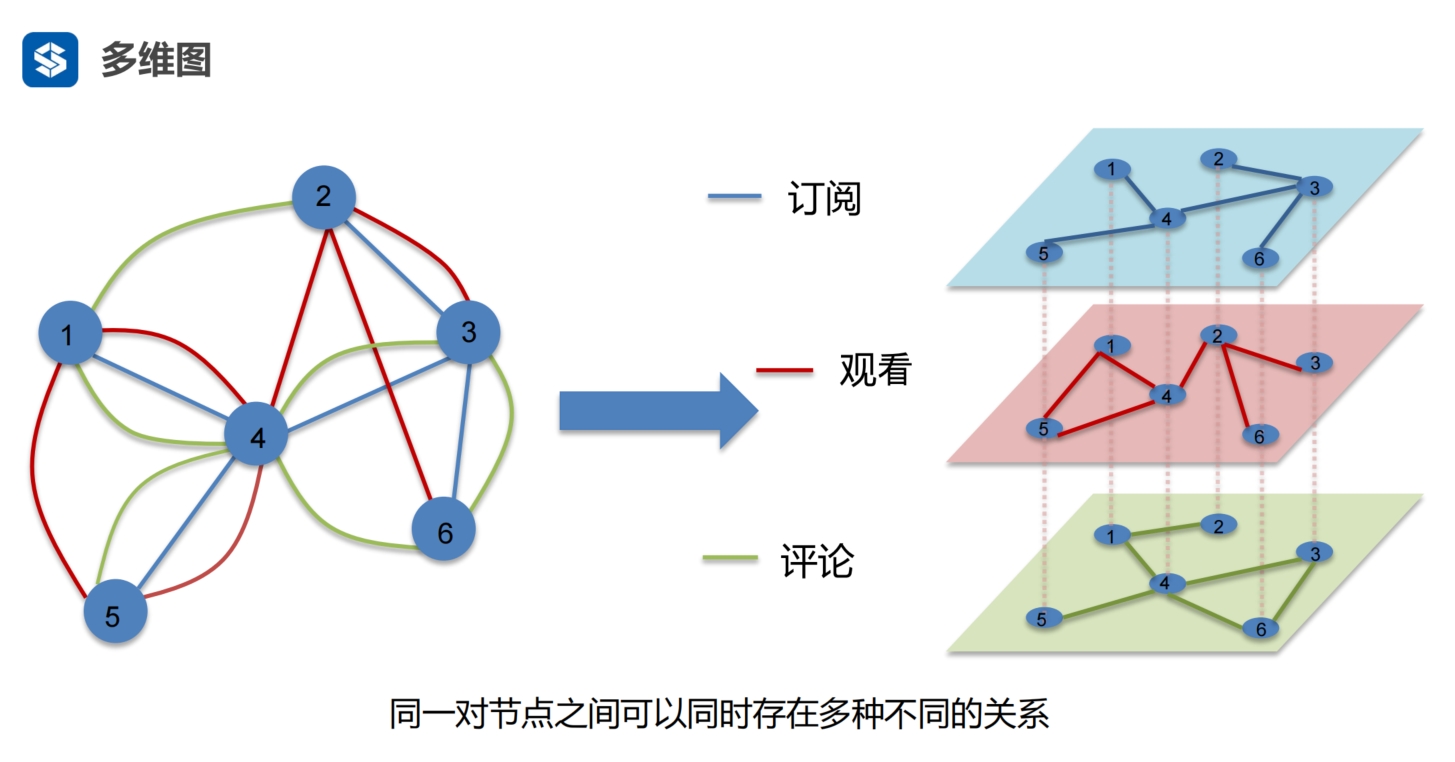
两个节点之间可以有多个边,每个边代表着一种关系 每一种关系相当于看节点的一个维度,即从不同的维度看节点 |
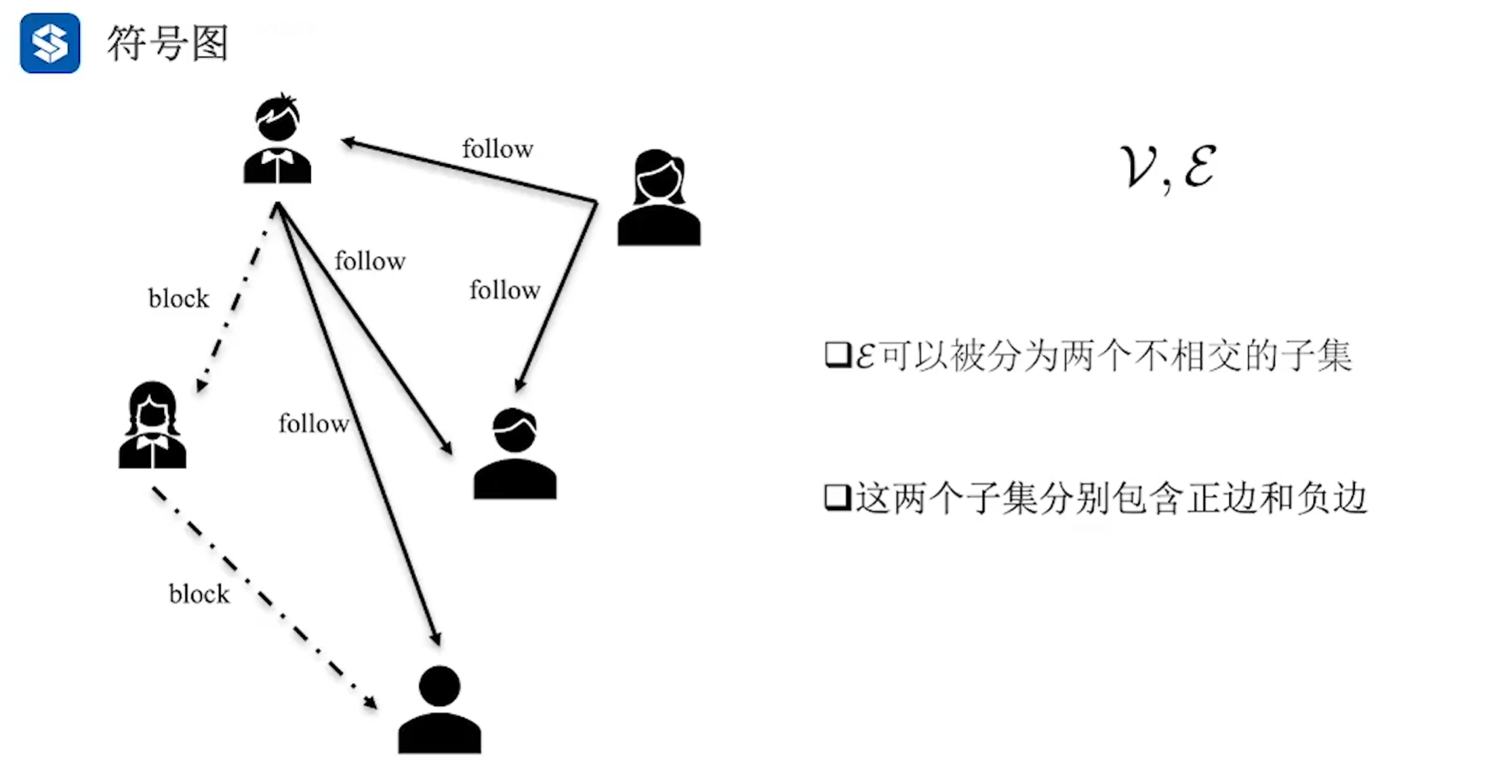
将边分类,比如 好友是一类,拉黑是另外一类 ,前者为正,后者为负 符号专指 +-正负符号,特指一个事物中正负两种关系 |
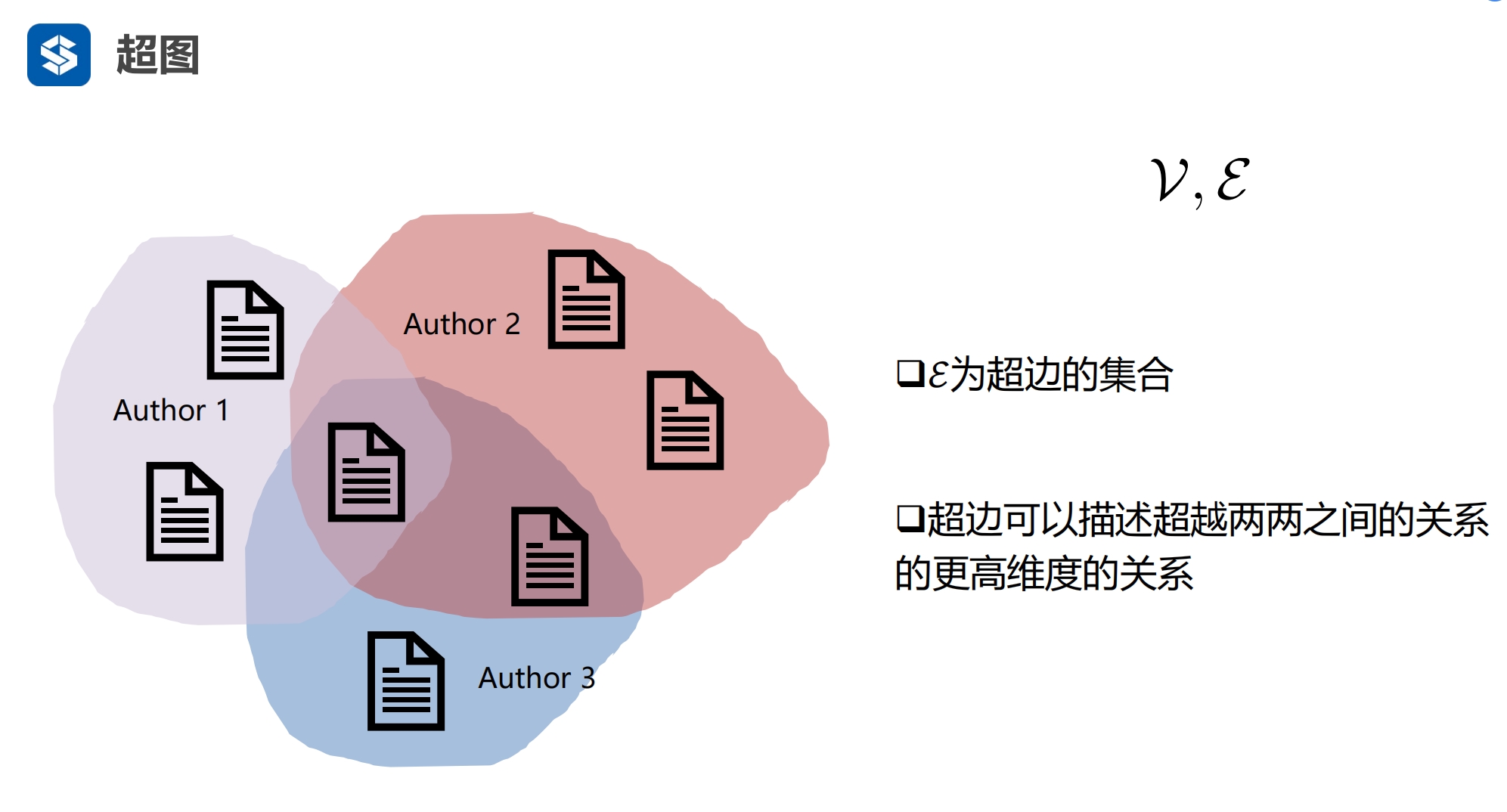
三篇文章的作者是一个 Author 1 就是一个超边,链接了三篇文章 - 前面图中的一个边,只链接了两个节点 |
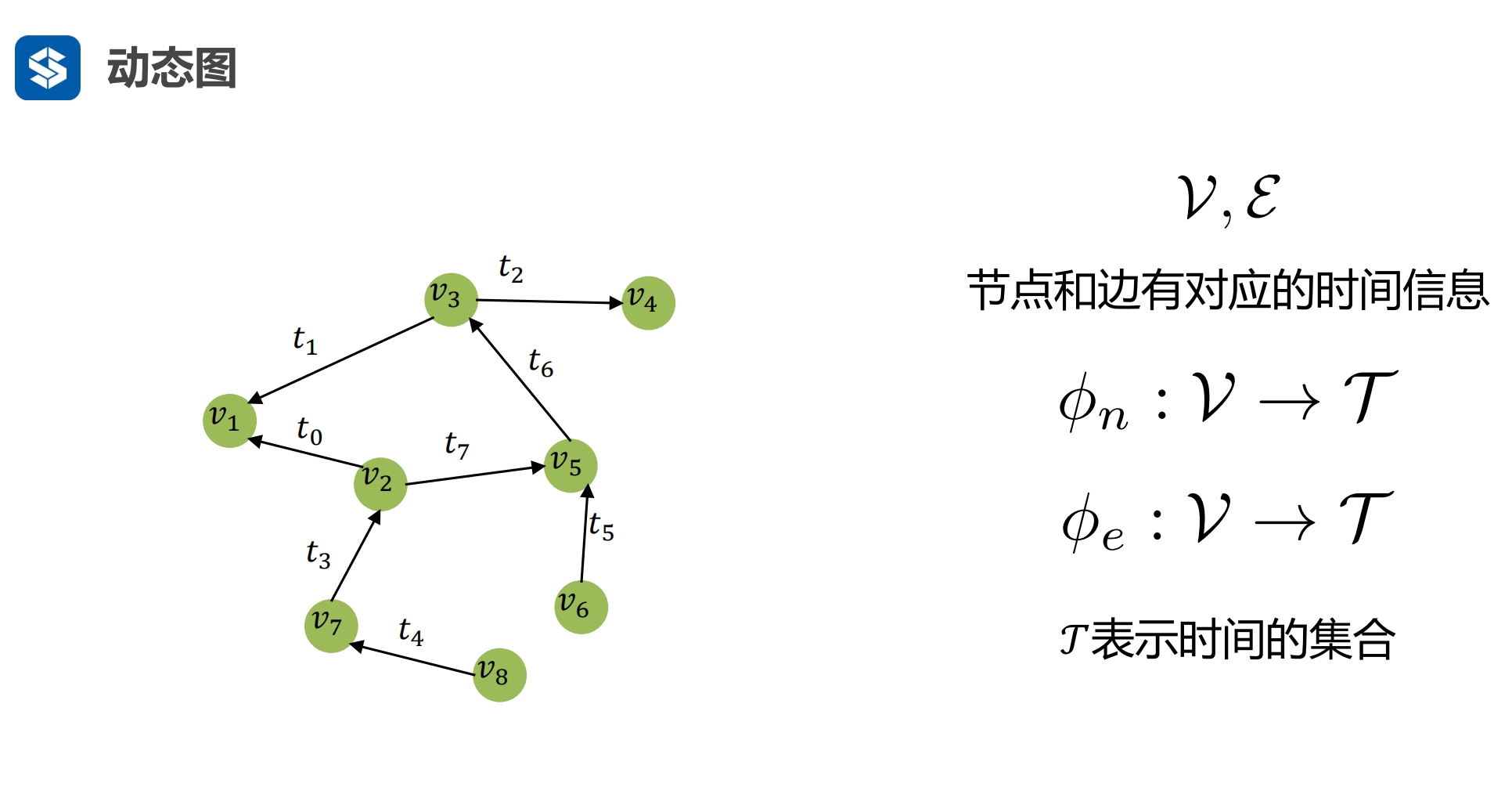
社交图 - 不同的时刻,用户节点数不同,用户有来有走 将节点映射到一个时间函数上 - 用户是什么时间加入进来的 - 边是什么时间建立的 这样的图是变化的,也叫流图 - 时间是离散的,1月份,2月份,... - 由月份到月份之间的数据是变化的,但也是离散的 |
|
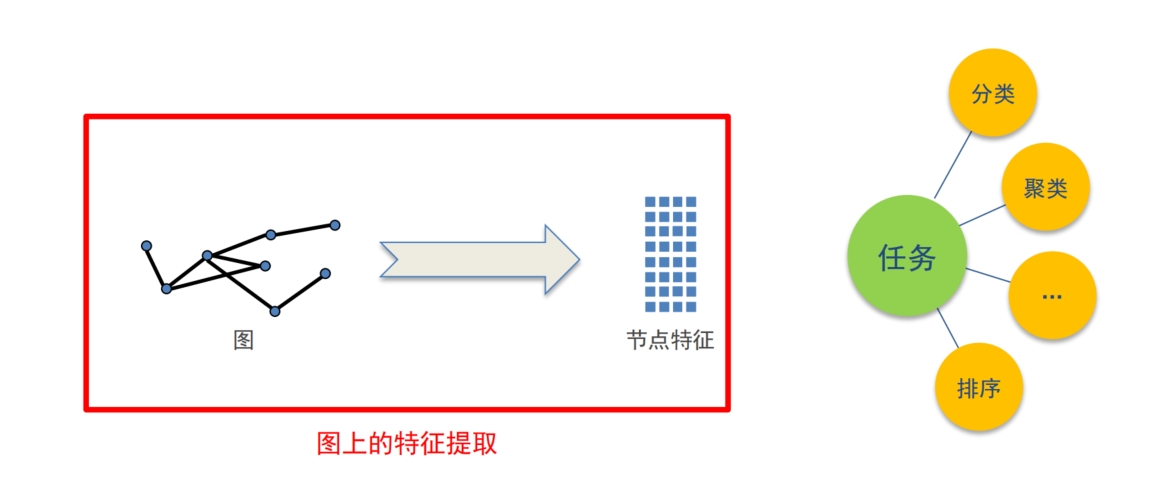
图嵌入·通用框架
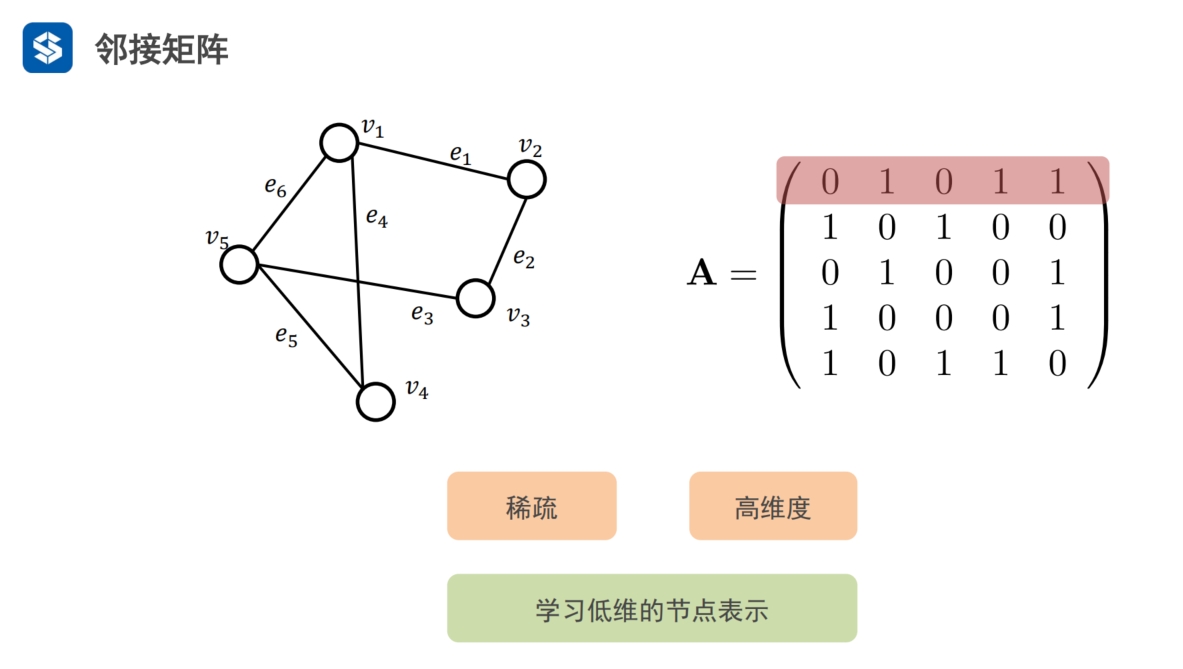
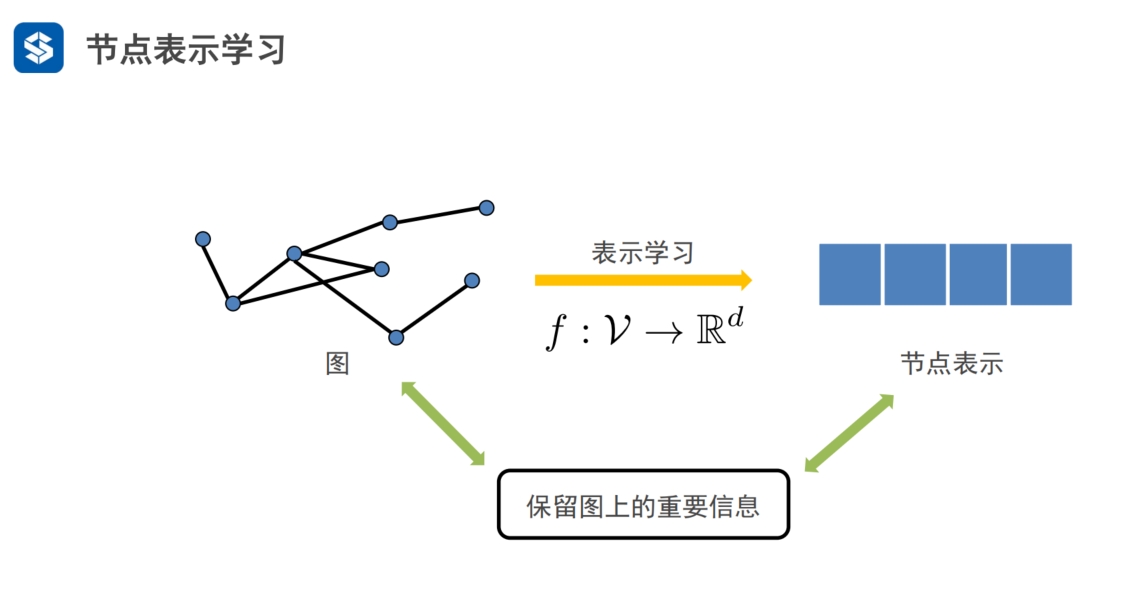
邻接矩阵用向量表示节点
- n维向量表示n个节点的图,如果图上节点个数多,则向量维度较高
- 度:社交,大部分人只有几个,几十个 好友
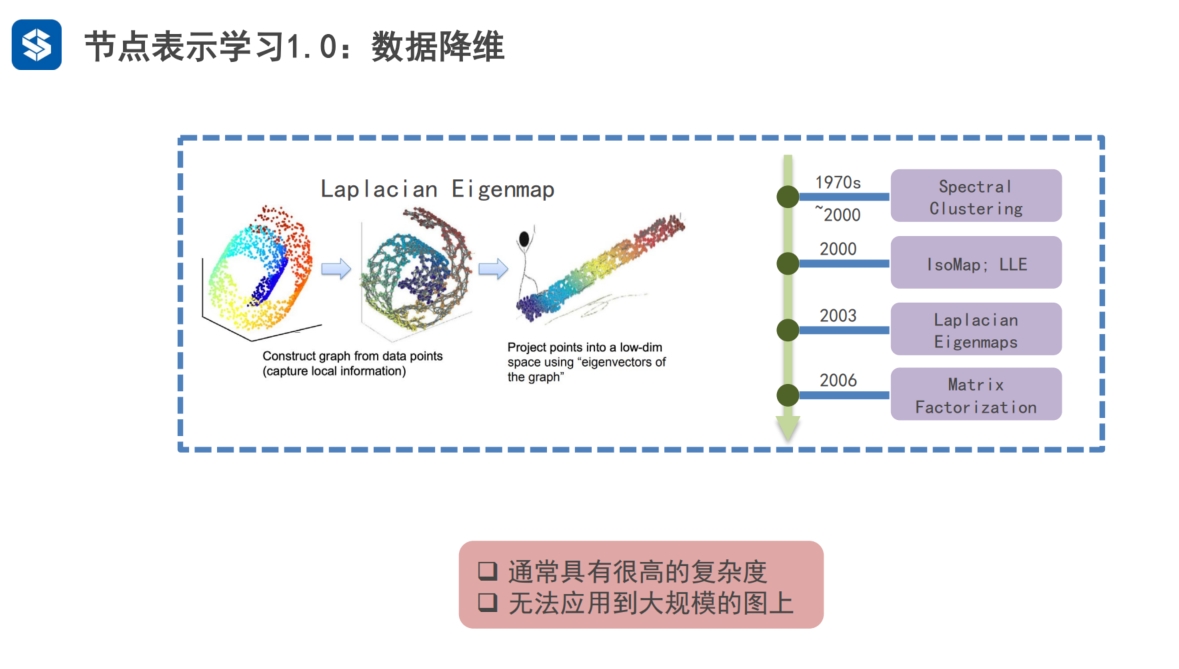
用一个函数将节点信息映射到低维空间 f: V--R
- 保留重要信息的前提下,表示用的维度尽量低
|
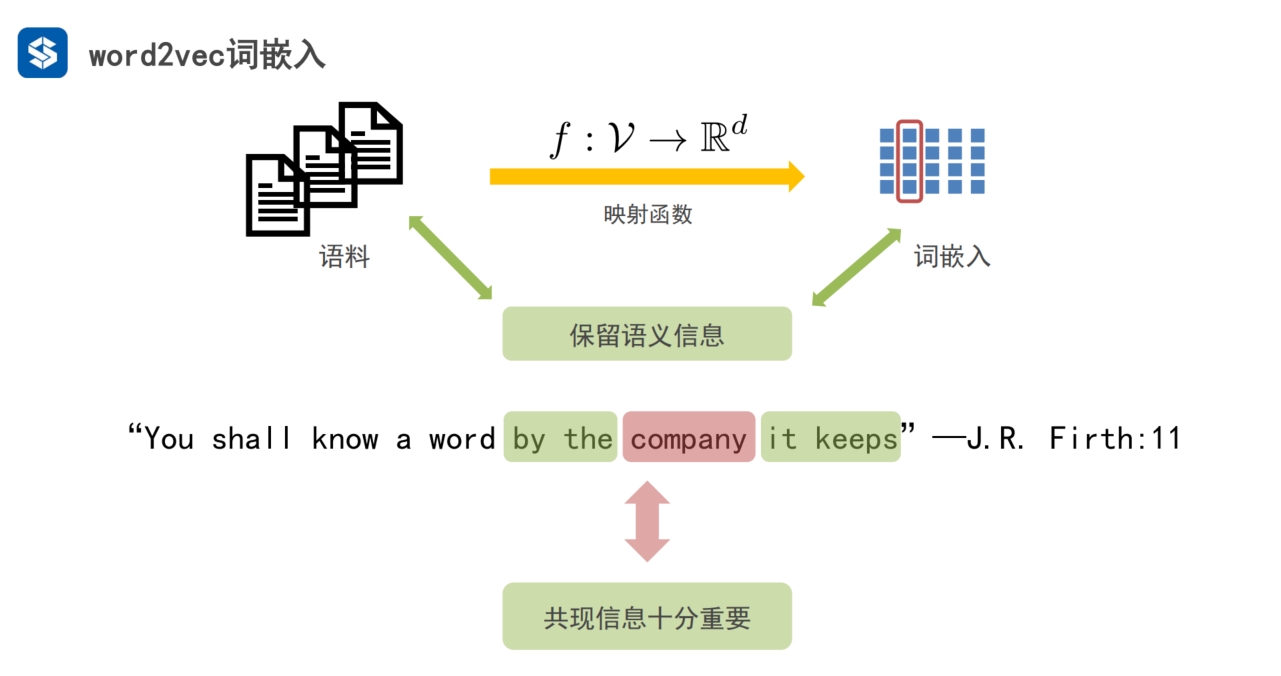
文章,段落,句子,单词
将单词从类似one hot这种高维空间映射到低维空间
- 映射的过程中,尽量保留原有的语义信息
- 这里的语义,更多的指上下文信息,即前一个词是什么,后一个词是什么
- 共同出现的信息,叫共现信息
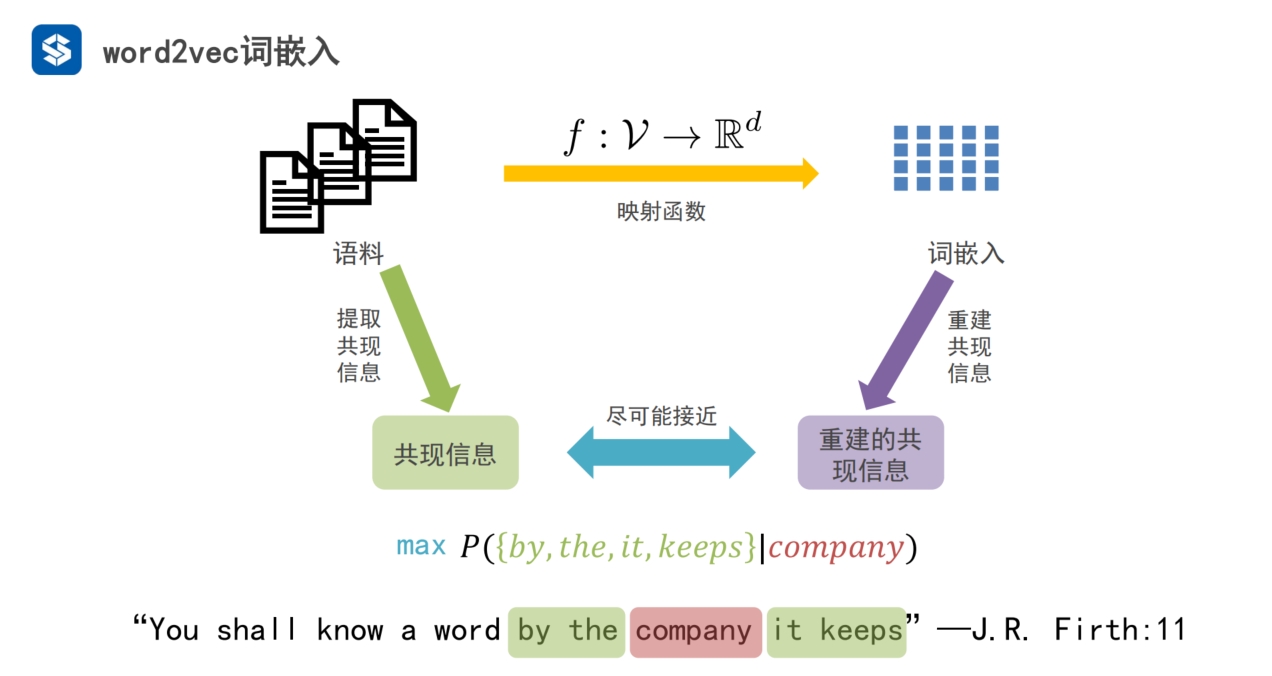
中心词
- 以某个词为中心,以step=1为窗口,就是提取中心词前一个单词与后一个单词
- 这就是词嵌入方法的基本思想
- 通过这种方法,保留单词的基本信息
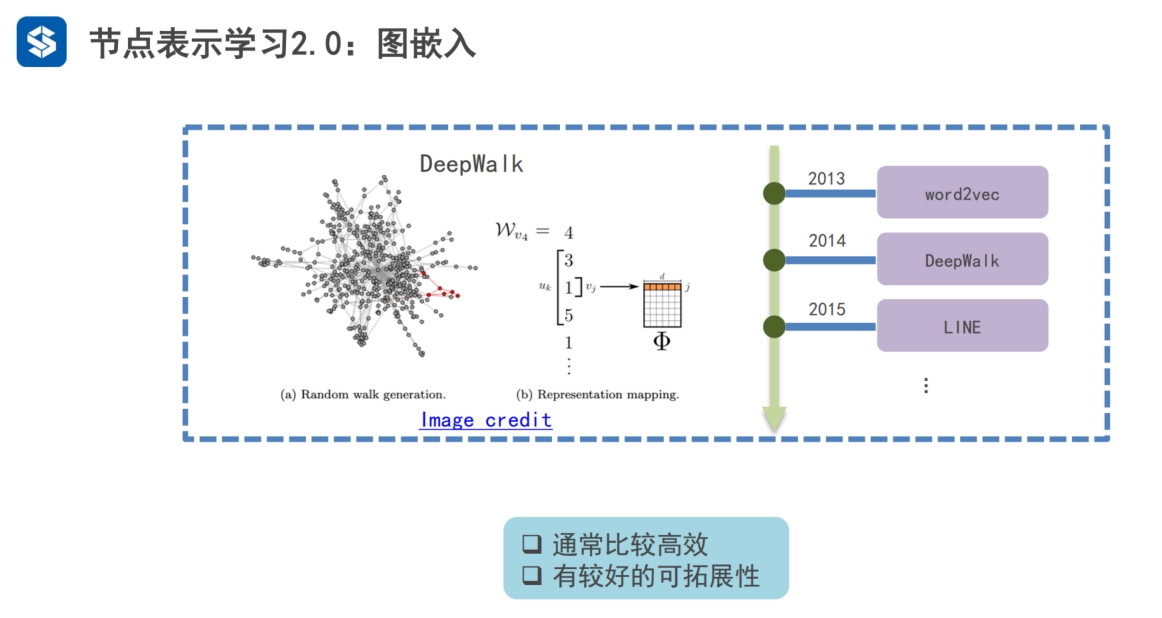
|
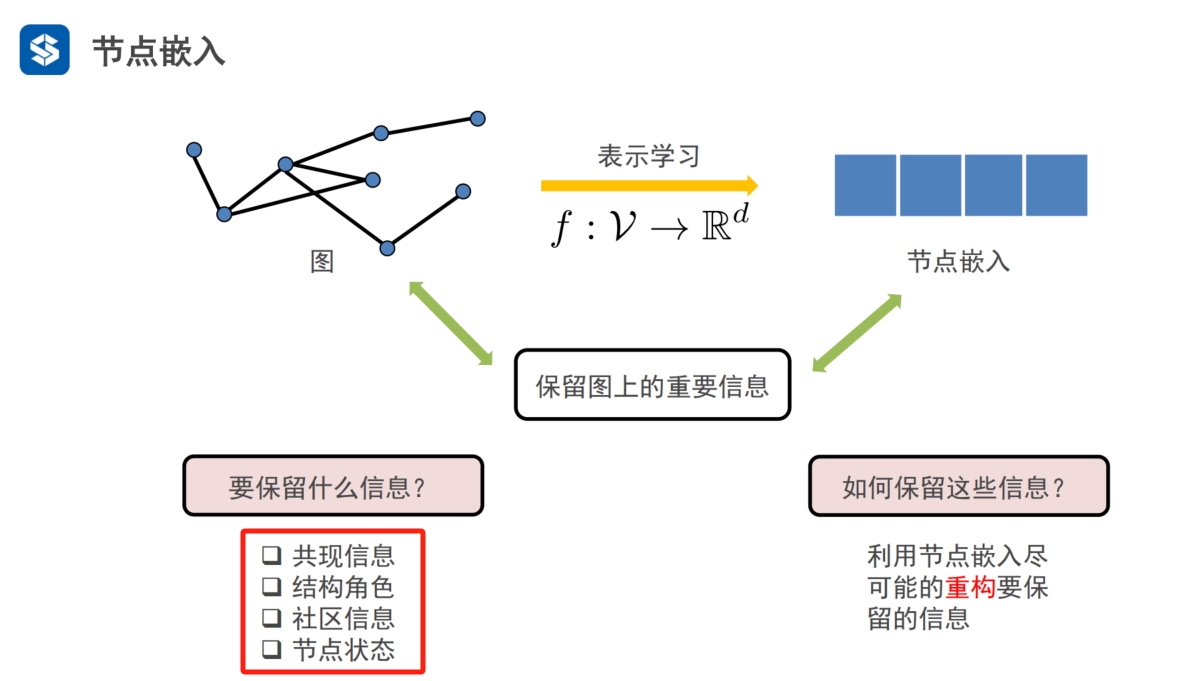
1. 将信息从 图域 映射 到 向量特征空间/嵌入域 2. 保留重要信息: 共现信息(上下文信息),结构角色,社区信息,节点状态 |
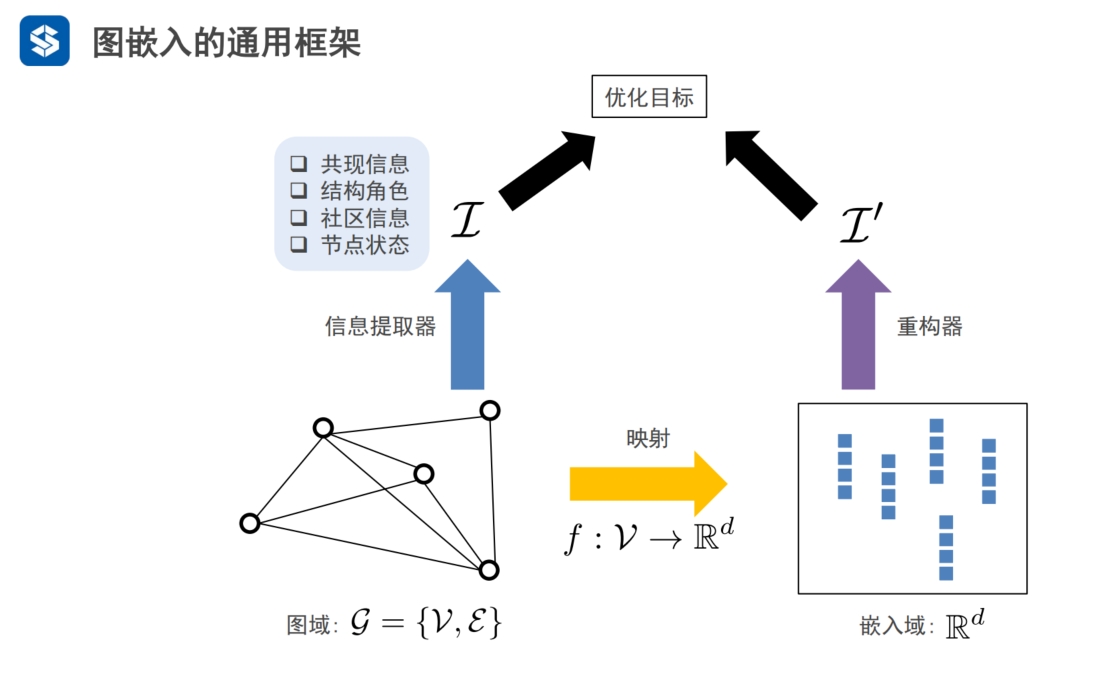
|
|
|
简单图嵌入
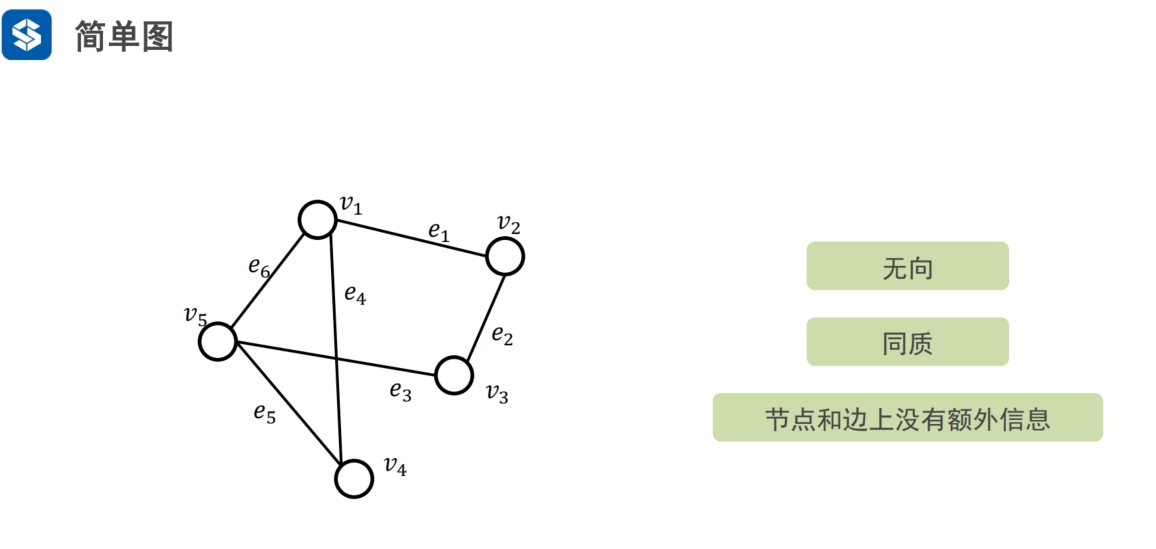
邻域,共现信息,相邻的信息,对应word2vec中的上下文信息
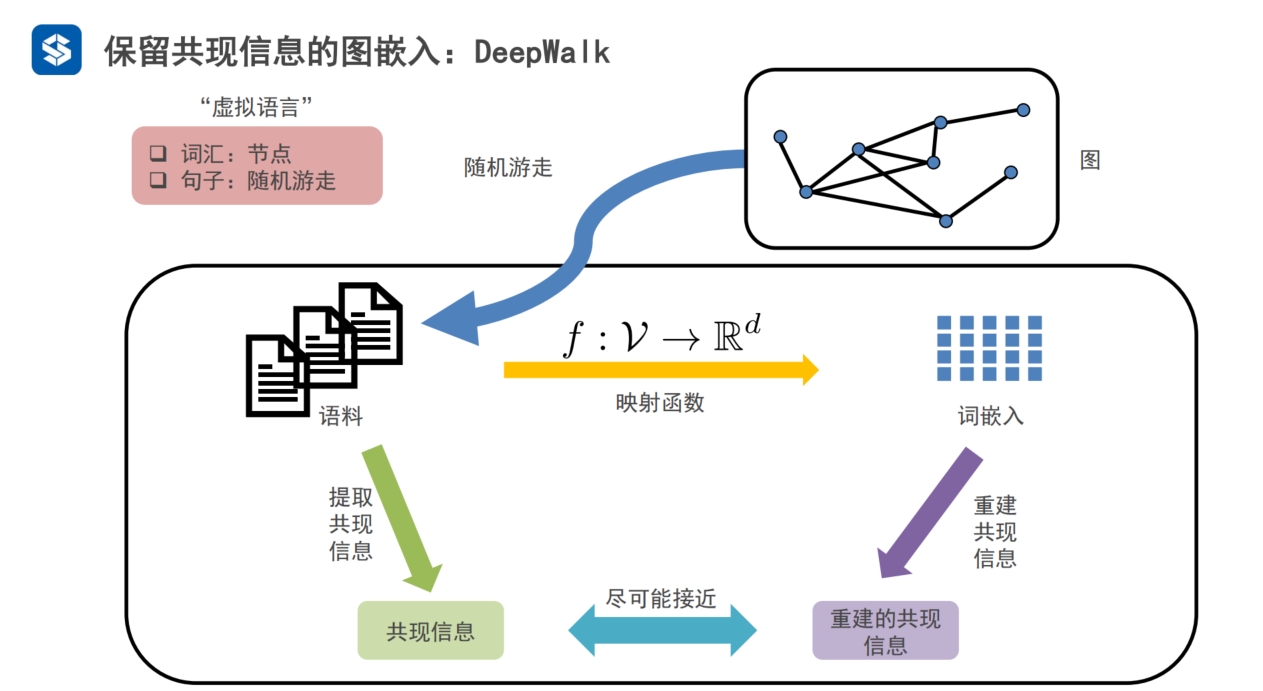
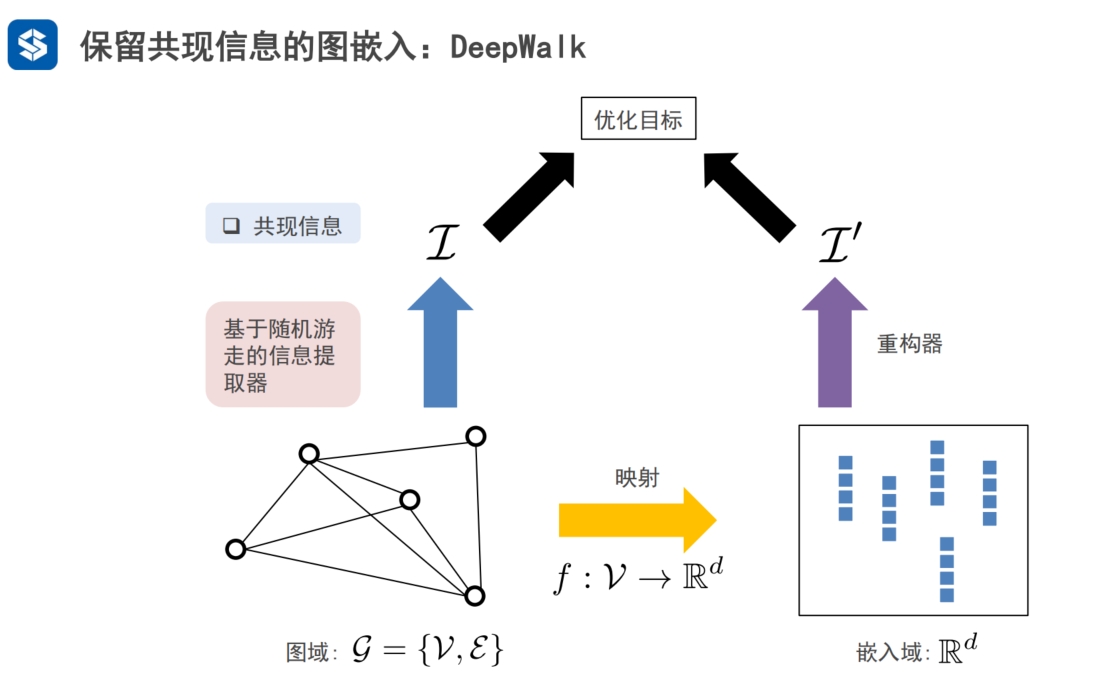
deepwalk的映射函数
- ei为单位矩阵E中第i列
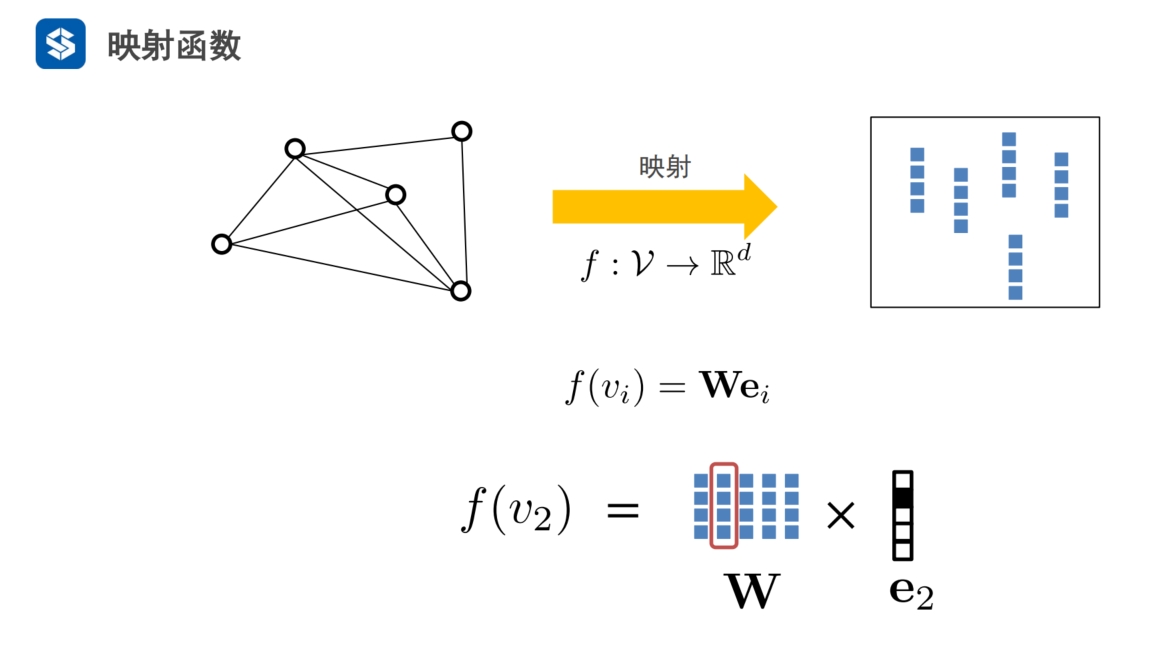
ei从W中提取第i个节点的向量特征,W是要学习的特征
|
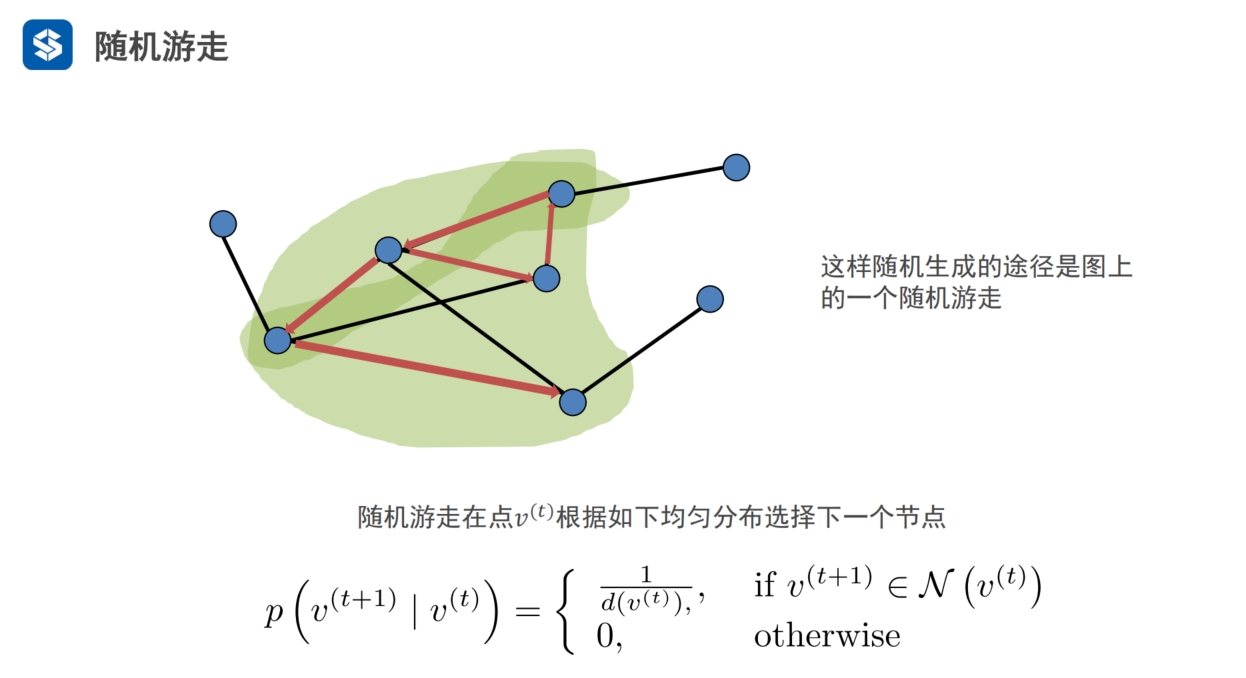
deepwalk通过随机游走的方法,产生一个序列,该序列对应着一个句子
N表示均匀分布
从当前节点到下一个节点
- 按度处理,节点之间的概率相同,等比
有了序列之后,就可以提取共现信息
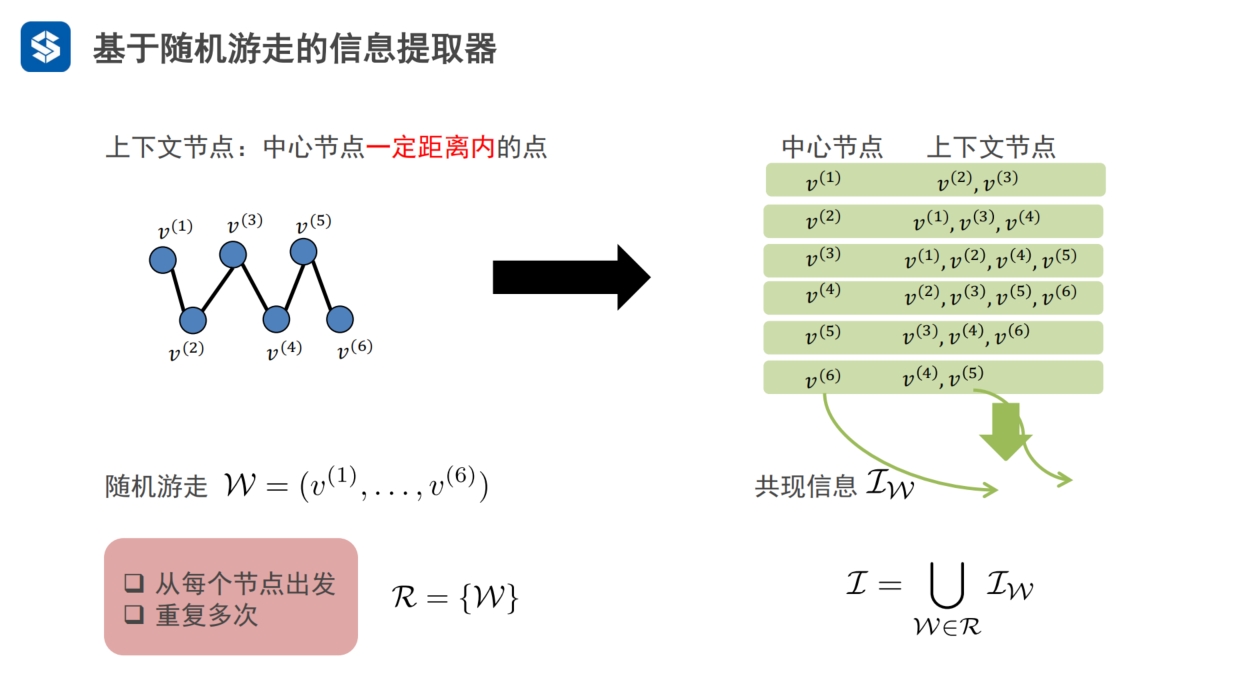
每个随机游走W就是一条途径,节点的共现信息为IW
从每个节点出发进行随机游走得到多条途径R={W}, 每个途径都对应一个共现信息IW,
- 这些共现信息并起来称为I
- I就是通过随机游走,在图中提取出来的节点,及节点的共现信息
|
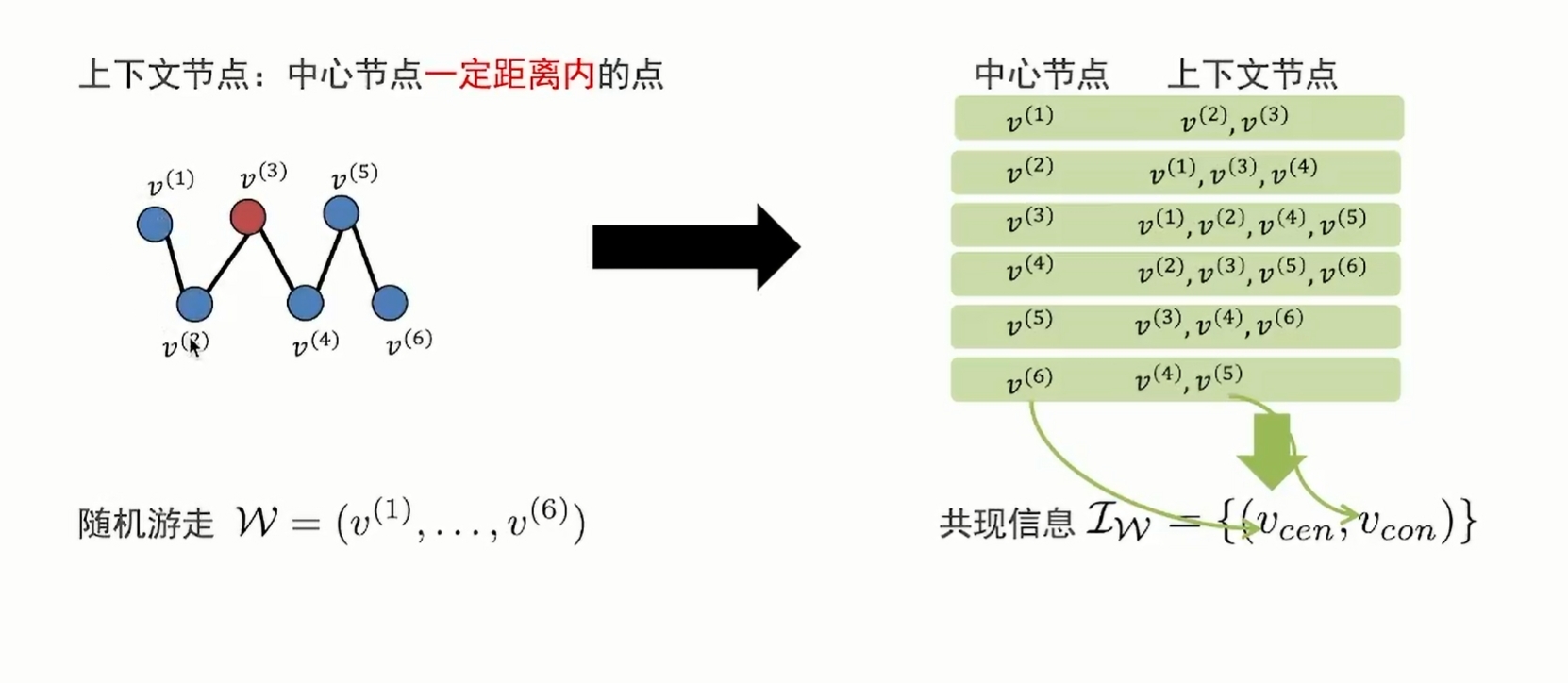
共现信息IW是基于随机游走的,是随机的序列
- 共现信息是集合
右边嵌入域融入概率信息
- 概率是基于统计
- 上下文序列上的概率,成对出现的概率
中心节点只有一个节点
上下文节点有多个节点,这就是上下文节点
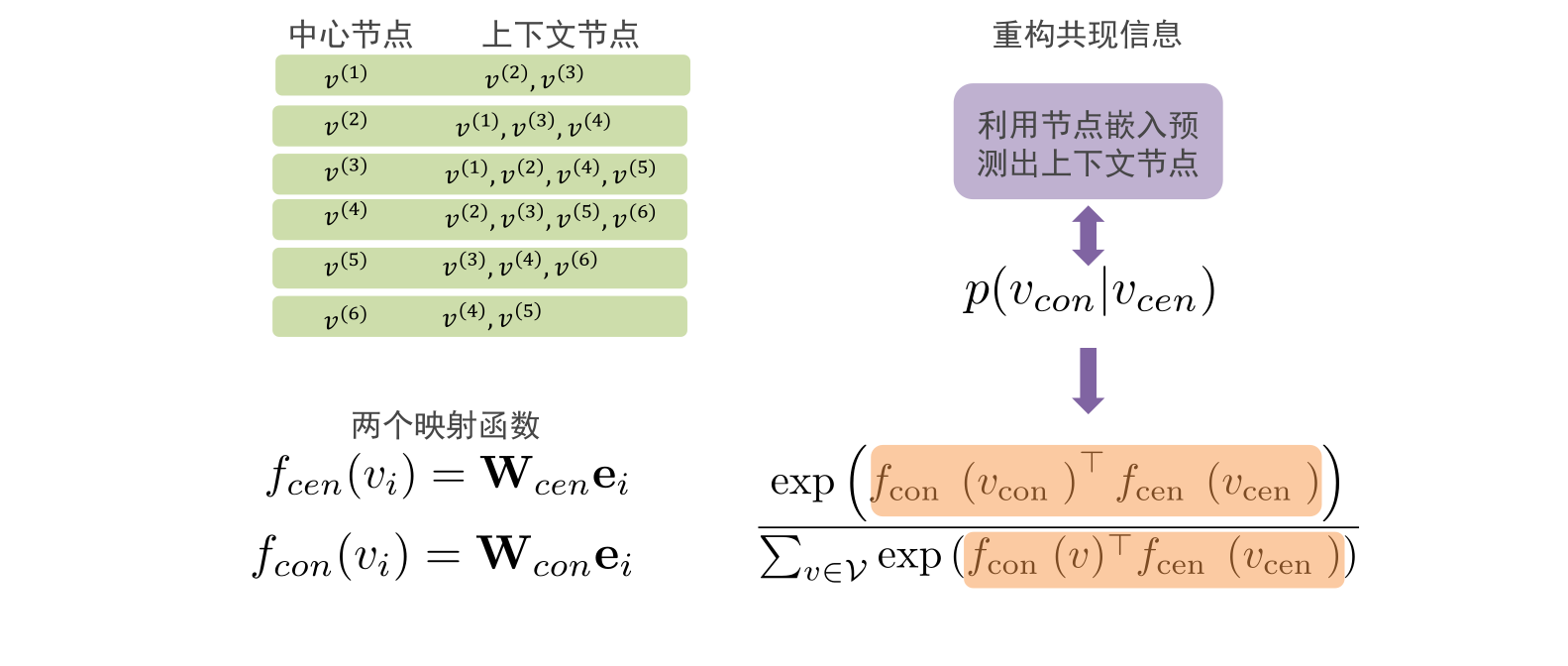
在deepwalk中,这两类节点,每类都对应一个初始化参数矩阵W
通过向量内积计算中心节点与上下文节点之间的相似性,
- 余弦相似度,越相似的两个单位向量,其内积越接近1
- 所有节点与其上下文节点的相似度的和为分母
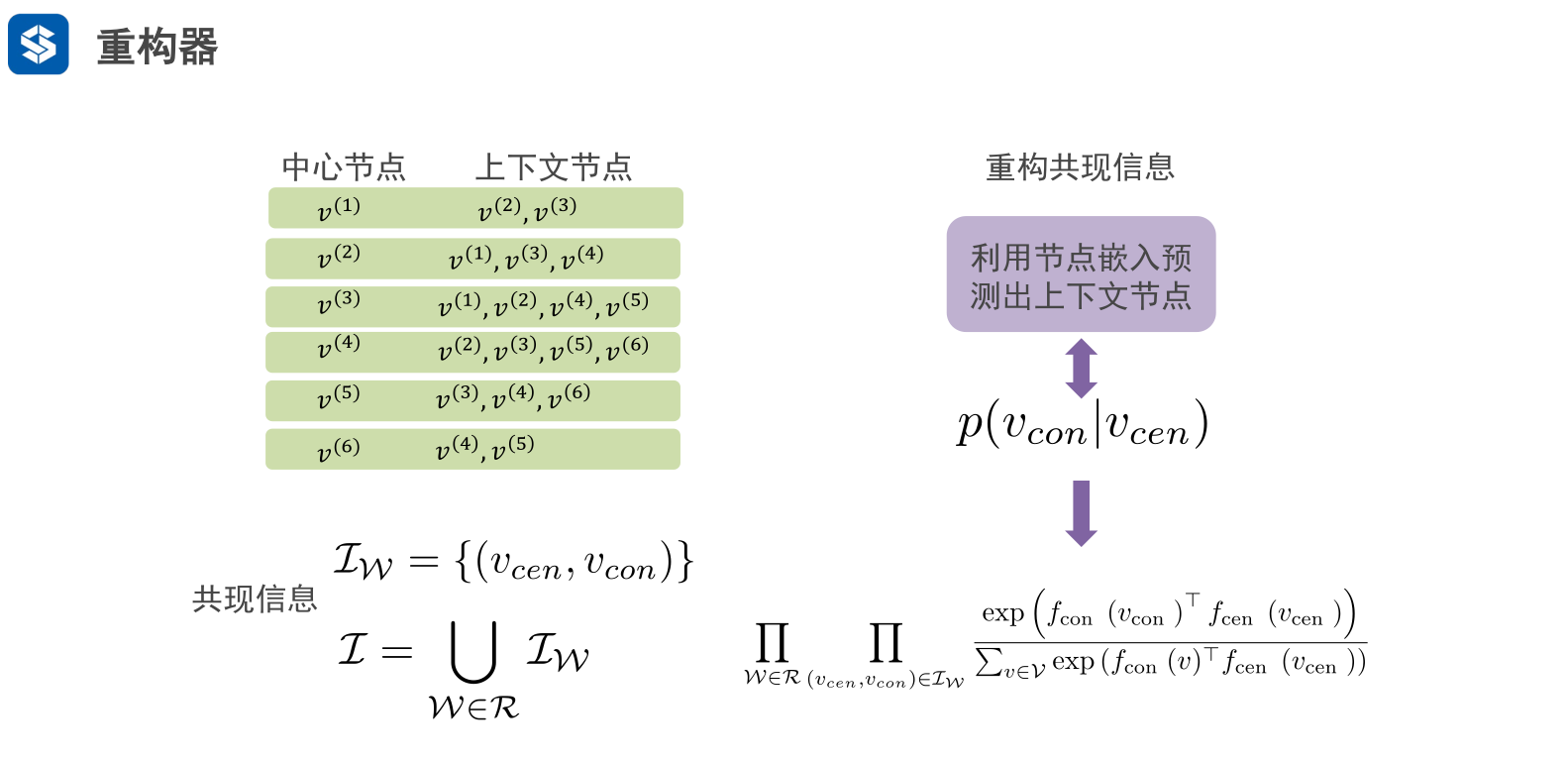
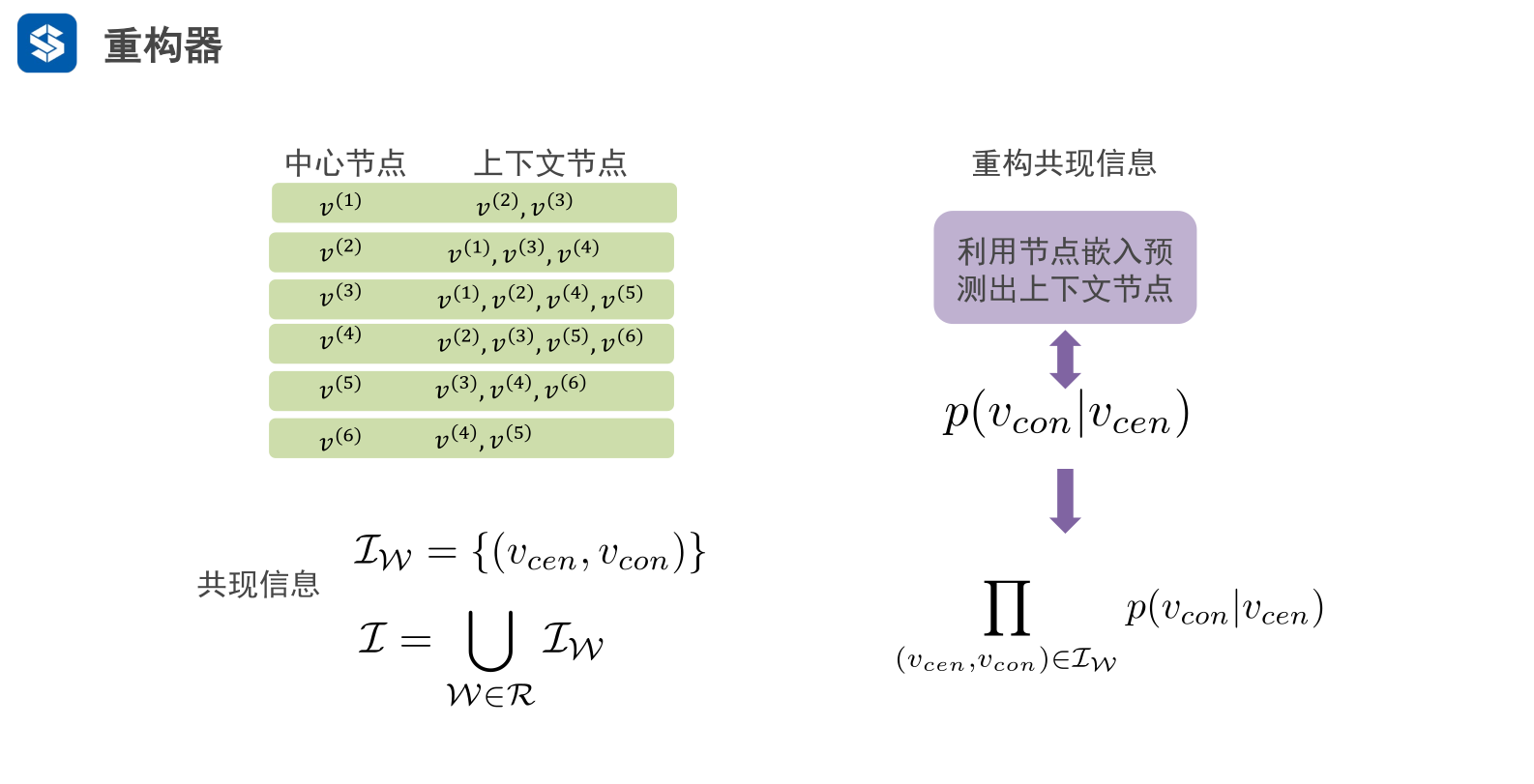
目标函数
共现信息中直接从图中提取出来的
通过初始化参数矩阵W及概率对构成的嵌入域并不与共现信息对等
如果让嵌入域中的节点向量接近共现信息中节点的真实含义?
- 嵌入域尽可能正确地预测共现信息
- 希望嵌入域中这个包含概率的计算公式的最大化 就是 真实的共现信息/ 接近共现信息
- 对应统计学中的最大似然估计
- 使用log转化,将连乘改为求和,并转化为最小化问题
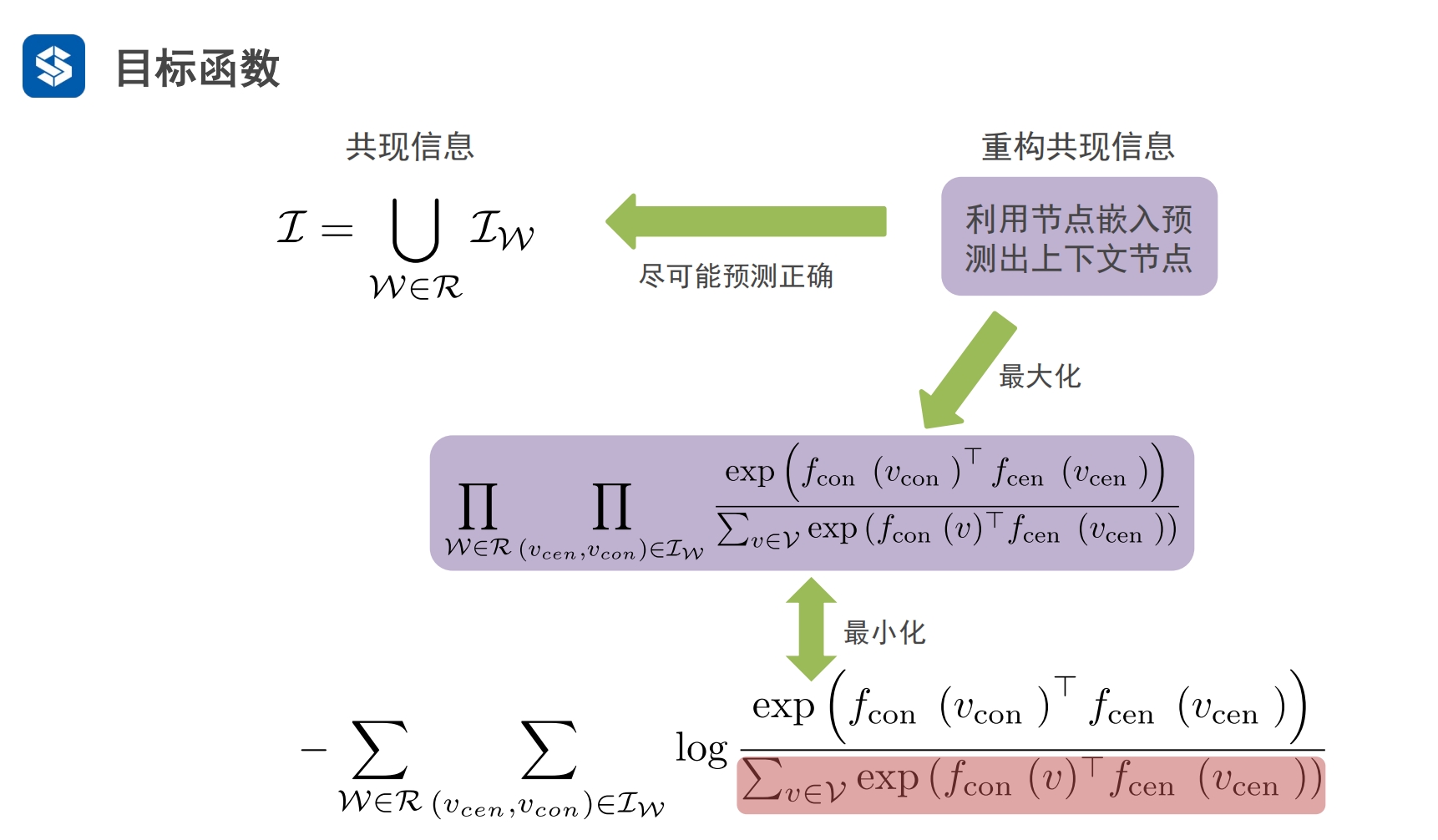
W是随机游走的路径,R是多个路径W的集合
IW是 单条路径W中 由(中心词,邻接词)构成的组合,代表中该路径中的信息
I 代表多条路径W中信息
有了邻接词可以推断中心词,有了中心词也可以推断邻接词
核心目的还是 将图中相邻节点的概率 转化为 节点对之间的概率
|
在大规模中节点多,相邻节点内积运算计算量大 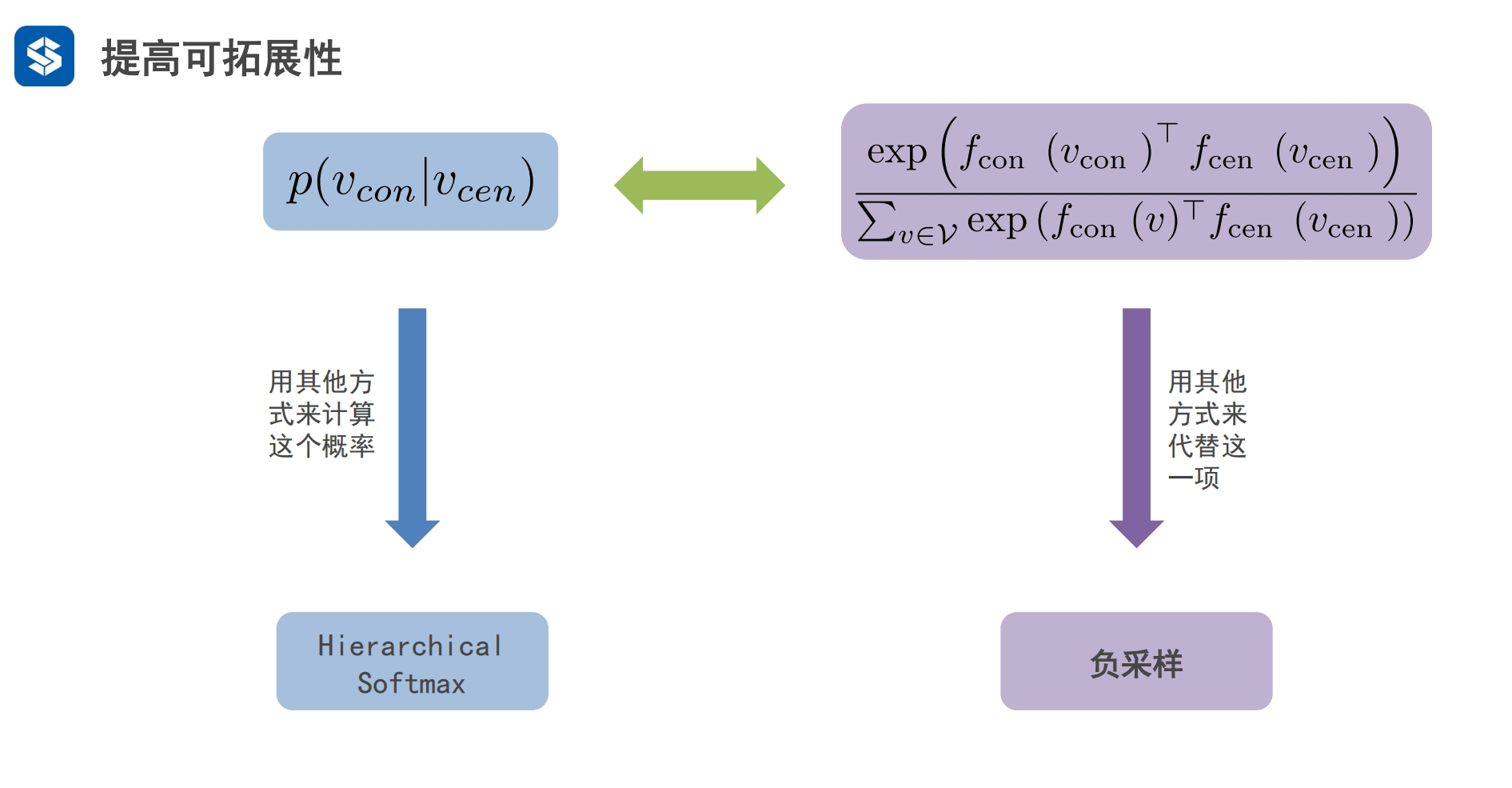
同维度对比,比如都是softmax,有没有速度更快的softmax 其他维度:负采样 - 字典的维度可以看作节点的个数 - p(vcon|vcen)可以看作平级处理,计算机不知道vcen的上下文节点是什么, - 于是它会遍历所有的上下文节点vcon,来统计计算p(vcon|vcen) 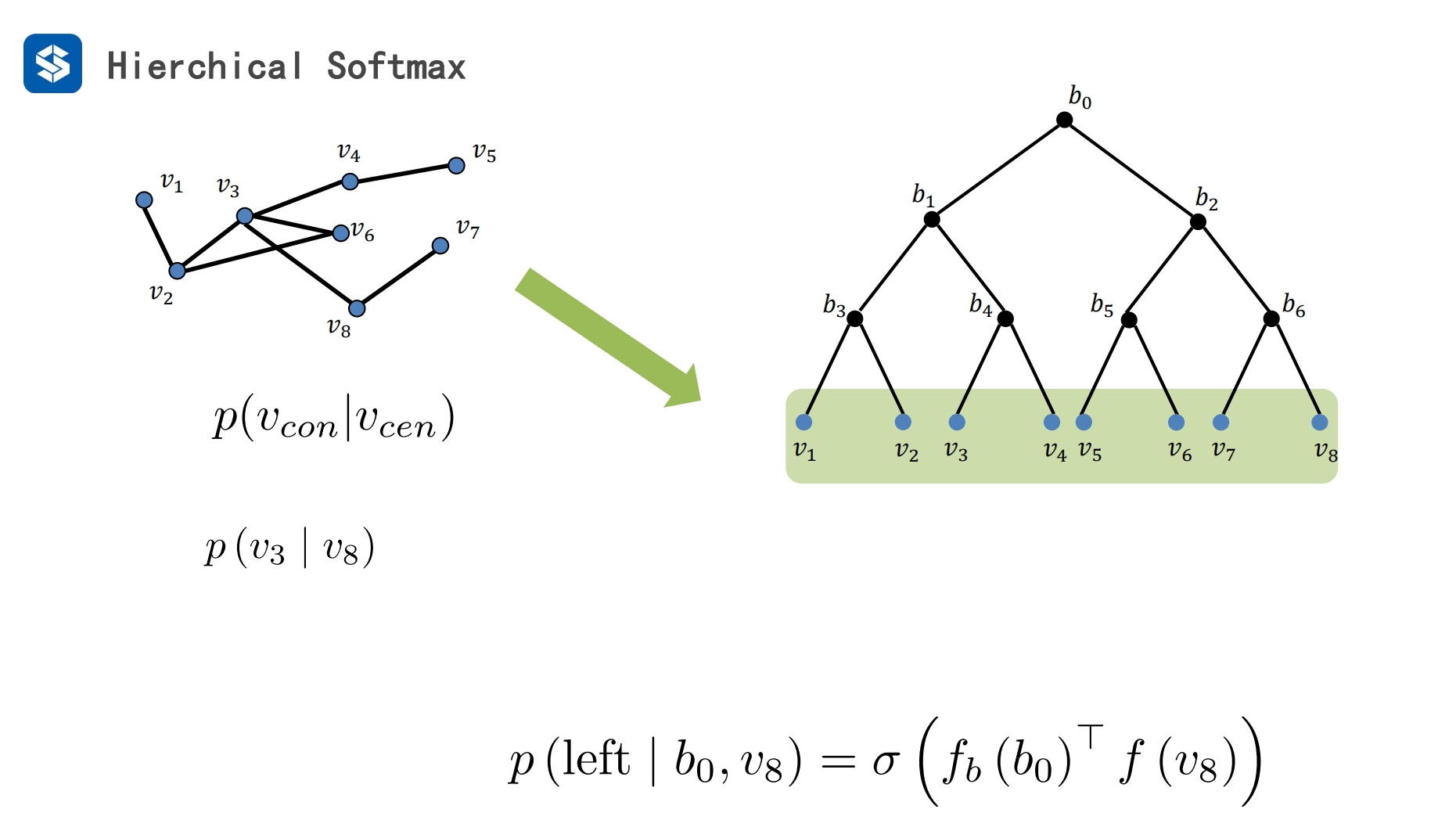
hierchical:层级结构 - 将搜索转化为二叉树 - 不再是全遍历 ,而是从根节点往下二分查找 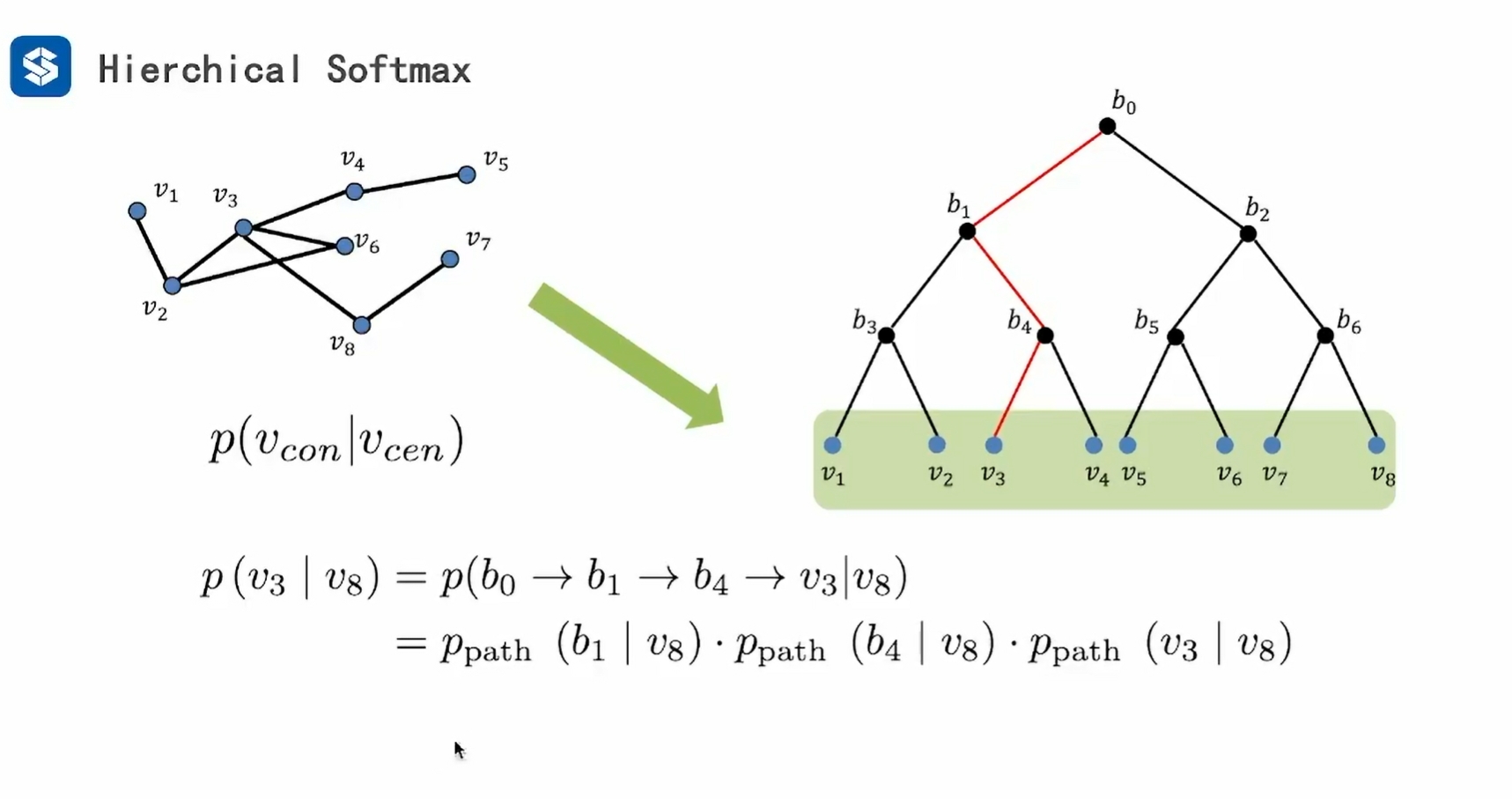

负采样 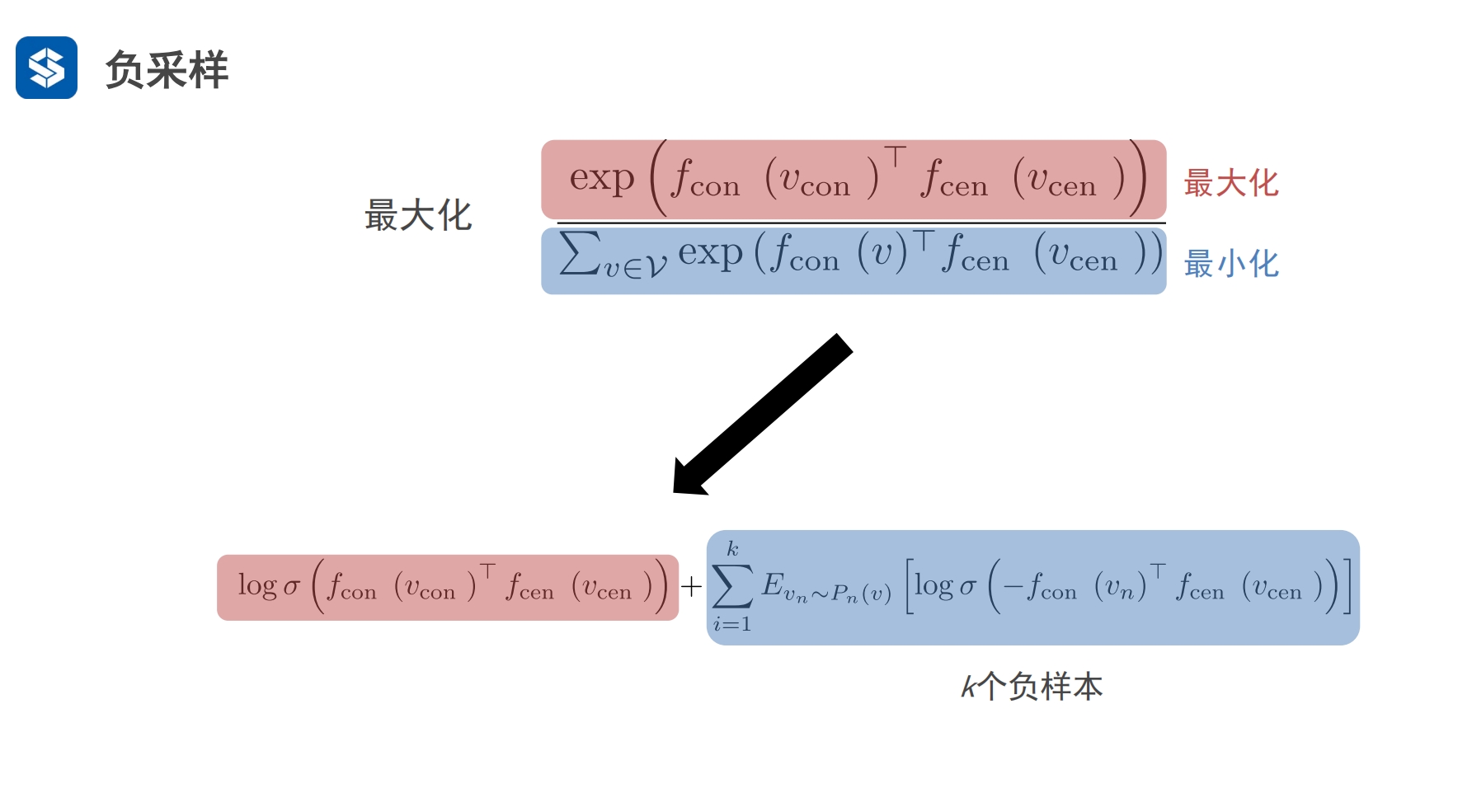
|
|
|
|
|
|
|
参考
神经网络】神经元ReLU、Leaky ReLU、PReLU和RReLU的比较