卷积的目的
卷积的目的在于提取特征,或者说卷积就是提取特征的一种方法
神经网络总体架构: 1. 提取特征 2. 分类 提取特征,层 在CV领域,提取特征的一种方法是 卷积 分类: 全连接 中间会穿插一系列增加模型拟合能力的方法: BN MAXPOOL RULE DROPOUT BN,RULE,DROPOUT在深度学习是通用的,不限于区域处理,这里先谈卷积与MAXPOOL
层与特征
层 : 分步
是什么是层,AI中的层,CV中的层? 一层指 神经网络中的一次综合计算,比如一次卷积计算就是一层,通常占一行代码的位置 层更侧重分步,这样一个神经网络: 1. 一个卷积 提取特征 2. 一个全连接分类 那个这神经网络就是两层
特征:分类
特征侧重的是分类, 比如一个向量的元素个数是n,处于n个不同的维度上, 重在强调差异性上,所以才是 “特征” 卷积API必不可少的两个参数就是: 输入特征,输出特征 - 输入特征,重在告诉API数据有多少个维度 - 输出特征,要提取出多少维度的特征, 这里,每一个特征,都是所有输入特征综合的一个计算结果, 是全体数据集某种计算方式的一个输出 广义上讲,层也可以用来划分类别,从不同层面描述事物时,其实就是分类, 所以,特征有时也叫特征层 但若提到神经网络的层数时,则指是分步
卷积核
一个像素有[R,G,B]三色,也可以说数据有三层, 卷积核对应也有三层,即,每个数据特征层对应一个卷积核, 每一层上卷积核的参数是随机初始化,之后再学习训练 卷积API要求输入特征数,因为要用这个参数初始化卷积核的层数,
卷积如何提取特征
原事物A有m个维度/特征/层,每个维度都对应一个矩阵,也叫特征图M[m1,m2] 每个卷积的输入皆是m*M的数据,是输入原事物所有特征的信息, 通常是所有特征的特征图计算完后,将m个计算结果相加 事物A与一个卷积进行n次计算,每次计算的网络参数都随机初始化, A 与卷积1线性计算一次,得到一个新的特征图M1[m1,m2](卷积通常不改变特征图shape) ... A 与卷积n线性计算一次,得到一个新的特征图Mn[m1,m2](卷积通常不改变特征图shape) 如此,原事物A的m维就转换到了n维 ,其shape由[m,m1,m2] --> [n,m1,m2] 这就是卷积的大致计算过程,在API还不熟悉的情况下,理解到这一步足够用,下面从其他角度再反复描述一下 卷积提取特征 提取的特征越来越多,每个特征图包含的信息越来越纯/少(毕竟总体信息不变,用于表示的量多了,每个量上的信息就会少), 就像线性方程组变换消元一样,在消元的过程中,每一行的(特征)变量在减少,在纯化, 如果有解,最后每一行化为xi=bi的形式,不再是多个特征变量线性混合映射到一个数,比如: x1 = 2 x2 = 5 .... 特征提取,特征提取,如何提取? 就是从多个维度去过滤/计算,一个维度过滤出这个维度的信息,其他维度都不要,最后过滤出来的特征图,信息量小了,但相对较纯 举例 要复制一款药物,说明书上列出七种成份, 你有十个仪器, A仪器用于检测是否含有a成分药物及多少,是否含有其他成分检测不出来 十个仪器检测下来,你检测出了六种,其中五种在说明书上,一种未在说明书上列出 这就是特征提取,逆向提纯一个 复杂事物,得到其 组成结构 (数学理论对应线性回归,回归其基本组成,但要知道,并非所有事物的结构都是线性的,我们只是用线性结构去近似描述一切事物) 接下来是分析问题,找出哪里出了问题 还有一个组成你不知道是啥,说明你的检测能力有限,仪器种类不够, AI中就是模型不够好,有待提升
卷积提取特征步骤
从一张灰色图片说起
img.shape = [1,1,H,W] 1. 初始化一个shape=[3,3]的参数矩阵w 2. 从[H,W]矩阵的左上角开始,取下[3,3]的一个子矩阵a 3. sum(a*w),按位相乘再相加,得到一个标量b1 4. 从[H,W]矩阵的左上角开始,向左走一步stride=1,取下[3,3]的一个子矩阵a2 5. sum(a*b),按位相乘再相加,得到一个标量b2 6. 重复以上过程,直到走完 (H-3 +1) 步, 此时得到一行数据 7. 向下移到一行,再重复以上过程,直到下移(W-3 +1)行
卷积公式
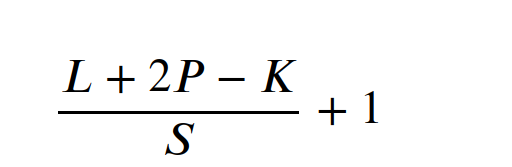
K 代表要取多少个索引上的元素作为核的一个维度/边长 2P P代表一边补0的个数,但两边都补相同的相数,所以是2P, 通常中左右相等,上下相等, 补完这个2P之后,(L+2P-K)/S 就会是一个整数 怎么就是整数了? 是因为要得到一个整数,然后去找了一个能得到整数结果的P值,输入进行, 然后才得了整数... 步长虽然是一步步走出来的,但逻辑上其实是多少等分的意思, 就是要分成多少份 每一份都是原来全体元素的一个局部,要与相同shape的参数矩阵按位相乘再相加,得到一个数, 这个数是某个视角上新的特征元素,它与原来的shape有位置上的对应关系
2维卷积
import torch
from torch import nn
from torch.nn import functional as F
"""以图像为例
2维卷积shape格式: [N,C,H,W]
N: batch_size 批量大小,一次处理多少个图像
C:channel 通道,也就是多少层,多少个特征,一张图像最小元素向量,即像素向量的元素个数
H:height 高度 也就是图像有多少行,一行有多少个像素,
W:width 宽度 也就是图像有多少列,一列有多少个像素
"""
X = torch.randn(32, 3, 256, 256)
conv2d = nn.Conv2d(in_channels=3, #输入数据层数/特征数是 3
out_channels=16, #每个卷积核3层,进行16次卷积核运算,得到16个特征
kernel_size=(3, 3), #一个卷积核是一个3*3的方阵
stride=(1, 1), #上下左右一次走一步
padding=(1,1), #上下左右各补1层
bias = True, #使用偏置,默认为true
padding_mode='zeros')#补的位置填充0,默认为0
conv2d(X).shape torch.Size([32, 16, 256, 256]) 3 1 1 是一种经典计算,实际上可尝试不同的数值 图像上要表达的核心信息在 中央,这种核的补法/设计,最大程度地保留了中间的信息
1维卷积
2维卷积,卷积核在两个方向/维度上移动,pytorch的2维卷积数据的shape为[N,C,H,W] 1维卷积,卷积核在1个方向/维度上移动,pytorch的1维卷积数据的shape为[N,C,L] 推广到3维,就是,卷积核在3个方向/维度上移动,pytorch的3维卷积数据的shape为[N,C,D,H,W] 3维不常用,这里只说1维
import torch from torch import nn from torch.nn import functional as F
"""1维卷积计算,自然语言处理,信号处理等
数据shape:[N, C, L]
N: batch_size 批量个数
C:channel 通道数
L:length 长度 序列的长度
举例:自然语言处理中:
N:句子,有多少句话
C:单词,每个单词向量的特征数
L:一个句子的单词个数
"""
# 32句话,每个单词128维,一句话10个单词
S = torch.randn(32, 128, 10)
conv1d = nn.Conv1d(in_channels=128, out_channels=256, kernel_size=3, stride=1, padding=1)
conv1d(S).shape
torch.Size([32, 256, 10])
卷积与全连接
全连接是一次计算所有参数与所有数据同时计算 卷积每次计算的时候,是一个卷积核的参数与对应的数据进行计算, 单次计算的量比全连接低一个档次,但总体的计算量要高于全连接
局部分块计算的顺序
相比全连接,卷积是一种流式计算,因为一次只计算整体数据的一个局部,
同时,卷积看似有顺序,即将数据分成一个个数据块-子矩阵,然后依然计算, 实则每个子矩阵计算完就是一个数值,最后是这些数值相加, 这意味着 实则无序,这些拆分后的子矩阵之间无顺序上的依赖关系, 先计算哪个分块,后计算哪个分块,结果一样, 比如来回跳着走,最后相加后结果一样, 所以卷积可以并行计算
新旧特征图位置对应关系
但卷积的确有位置对应关系,这种映射关系是指, 原数据shape的某个卷积核计算的位置与新特征图上元素位置一一对应, 比如2维图像上第1个卷积核计算结果必定是新的特征图上左上角的第1个点/数值, 是原特征图局部区域 与 新特征图元素位置的 一一对应关系
只要这种特征图位置对应关系不打乱, 每次按步长移动的计算,可以不按顺序计算,还可以并发计算
参考