numpy简介
https://numpy.org/ numpy使用C编写,贯穿整个机器学习,深度学习,人工智能 你可以用numpy自己实现一个自己的框架 numpy是针对 数据科学 而设计的,在计算机底层数据计算这一块有很强的优势, python 的数据类型,比如列表也能运算,但它并不专门为数据科学而设计,除了人工智能,还有很多其他行业,运维,开发... 学AI,必学numpy AI矩阵运算,要用numpy.ndarray或者其他AI框架的数组 python list不是专门为AI设计的,不要用这个进行矩阵运算 流水的框架,铁打的Numpy;
Numpy奠定了人工智能根基!
- 简单
- 高效
- 易用
- num:数据,py:python
- py表示是一个python模型,往往不是python写的,
- numpy由C语言编写
- python的上层接口+C语言的高性能计算
- 解放底层实现的代码编写,让人有更多时间去关注算法思想
sklearn:机器学习的杆竿,底层用了numpy
pytorch:numpy的增强版,提供了自动求导功能
|
ll lib/python3.9/site-packages/numpy
total 372
-rw-rw-r-- 2 xt xt 2179 May 30 2022 LICENSE.txt
-rw-rw-r-- 1 xt xt 3785 Dec 20 03:52 __config__.py
-rw-rw-r-- 2 xt xt 36238 May 30 2022 __init__.cython-30.pxd
-rw-rw-r-- 2 xt xt 34606 May 30 2022 __init__.pxd
-rw-rw-r-- 2 xt xt 16013 May 30 2022 __init__.py
-rw-rw-r-- 2 xt xt 133925 May 30 2022 __init__.pyi
drwxrwxr-x 2 xt xt 4096 Dec 20 20:19 __pycache__
-rw-rw-r-- 2 xt xt 774 May 30 2022 _distributor_init.py
-rw-rw-r-- 2 xt xt 2949 May 30 2022 _globals.py
-rw-rw-r-- 2 xt xt 6302 May 30 2022 _pytesttester.py
-rw-rw-r-- 2 xt xt 498 May 30 2022 _version.py
-rw-rw-r-- 2 xt xt 1715 May 30 2022 char.pyi
drwxrwxr-x 4 xt xt 4096 Dec 20 03:52 compat
-rw-rw-r-- 2 xt xt 4031 May 30 2022 conftest.py
drwxrwxr-x 6 xt xt 4096 Dec 20 03:52 core
-rw-rw-r-- 2 xt xt 17221 May 30 2022 ctypeslib.py
-rw-rw-r-- 2 xt xt 451 May 30 2022 ctypeslib.pyi
drwxrwxr-x 8 xt xt 4096 Dec 20 03:52 distutils
drwxrwxr-x 3 xt xt 4096 Dec 20 03:52 doc
-rw-rw-r-- 2 xt xt 2214 May 30 2022 dual.py
drwxrwxr-x 5 xt xt 4096 Dec 20 03:52 f2py
drwxrwxr-x 4 xt xt 4096 Dec 20 03:52 fft
drwxrwxr-x 4 xt xt 4096 Dec 20 03:52 lib
drwxrwxr-x 4 xt xt 4096 Dec 20 03:52 linalg
drwxrwxr-x 4 xt xt 4096 Dec 20 03:52 ma
-rw-rw-r-- 2 xt xt 10365 May 30 2022 matlib.py
drwxrwxr-x 4 xt xt 4096 Dec 20 03:52 matrixlib
drwxrwxr-x 4 xt xt 4096 Dec 20 03:52 polynomial
-rw-rw-r-- 2 xt xt 0 May 30 2022 py.typed
drwxrwxr-x 6 xt xt 4096 Dec 20 03:52 random
-rw-rw-r-- 2 xt xt 971 May 30 2022 rec.pyi
-rw-rw-r-- 2 xt xt 983 May 30 2022 setup.py
drwxrwxr-x 5 xt xt 4096 Dec 20 03:52 testing
drwxrwxr-x 3 xt xt 4096 Dec 20 03:52 tests
drwxrwxr-x 4 xt xt 4096 Dec 20 03:52 typing
-rw-rw-r-- 2 xt xt 371 May 30 2022 version.py
[root@ki /]# cat /ai/app/anaconda3/lib/python3.9/site-packages/numpy/__init__.py
"""
NumPy
=====
Provides
1. An array object of arbitrary homogeneous items
2. Fast mathematical operations over arrays
3. Linear Algebra, Fourier Transforms, Random Number Generation
How to use the documentation
----------------------------
Documentation is available in two forms: docstrings provided
with the code, and a loose standing reference guide, available from
`the NumPy homepage
|
|
矢量与向量
这是一道涉及数学概念辨析的问题。首先,我们需要理解“矢量”和“向量”在数学中的定义,然后对比两者的异同。
定义分析:
矢量:在物理学和工程学等领域中,矢量通常用来描述具有大小和方向的物理量,如力、速度和加速度等。在数学上,矢量是一个有序的元素集合,这些元素可以是实数或复数,并且满足向量的加法和数乘运算规则。
向量:在数学中,向量是一个更广泛的概念,它指的是一个具有大小和方向的量,通常用箭头表示。向量可以在不同的数学结构(如实数域、复数域、向量空间等)中定义,并满足特定的运算规则。
对比与关系:
从定义上看,矢量和向量在描述上具有相似性,都强调了大小和方向的特性。
在实际应用中,特别是在物理学和工程学领域,矢量一词经常被使用,而在更纯粹的数学语境下,向量一词更为常见。
从学科交叉的角度来看,矢量可以被视为向量在特定领域(如物理学)的一种具体应用或表现形式。
结论:
在大多数情况下,特别是在非数学专业的语境中,矢量和向量可以视为同义词,都用来描述具有大小和方向的量。
然而,在严格的数学定义中,向量是一个更广泛、更抽象的概念,而矢量则更多地与物理学和工程学等领域的实际应用相关联。
综上所述,可以认为矢量和向量在大多数情况下是等同的,但在不同学科和语境中可能有所侧重。在数学领域,向量是更通用的术语,而矢量则更多地用于描述物理学和工程学中的具体量。
科学计算就是 矢量/向量/矩阵运算, 矩阵运算通常以二维矩阵进行运算,二维矩阵以向量运算为单位 广播机制
向量运算的广播机制(Broadcasting)是深度学习和科学计算中常用的一种技术,特别是在使用NumPy、PyTorch等库时。广播机制允许在执行算术运算时自动扩展张量(或向量、矩阵)的形状,使其兼容,从而简化了代码编写并提高了计算效率。以下是对向量运算的广播机制的详细解释:
一、广播机制的基本原理
广播机制的核心是内容复制和按位运算。当两个张量的形状不匹配时,广播机制会尝试将其中一个张量的形状扩展到与另一个张量兼容,以便进行按位运算。这种扩展是通过在较小维度的张量前面添加1来实现的,直到两个张量的形状相同。
二、广播机制的规则
维度对齐:
两个张量在某个维度上的长度必须相同,或者其中一个张量在该维度上的长度为1。
如果两个张量的维度不同,则会在较小维度的张量前面添加1,直到它们的维度相同。
形状扩展:
在广播过程中,长度为1的维度会被扩展为与另一个张量在该维度上相同的长度。
这种扩展是通过复制该维度上的元素来实现的。
运算规则:
一旦两个张量的形状通过广播机制变得兼容,就可以对它们进行逐元素的算术运算(如加法、减法、乘法等)。
三、广播机制的示例
假设我们有两个张量A和B,它们的形状分别为(m, n)和(1, n)。我们希望将A和B相加。
张量形状:
A的形状为(m, n)。
B的形状为(1, n)。
广播过程:
根据广播机制,B的第一个维度(长度为1)会被扩展为与A的第一个维度(长度为m)相同。
因此,B的形状会被扩展为(m, n),与A的形状相同。
逐元素加法:
一旦B的形状被扩展为(m, n),就可以对A和B进行逐元素的加法运算。
四、广播机制的应用
广播机制在深度学习和科学计算中非常有用,特别是在处理不同形状的张量时。它允许我们避免显式的形状扩展操作,从而简化了代码编写并提高了计算效率。例如,在神经网络中,我们经常需要将一个标量(形状为())或向量(形状为(n,))与一个矩阵(形状为(m, n))进行运算。通过广播机制,我们可以轻松地实现这种运算,而无需手动调整张量的形状。
五、注意事项
维度不匹配:
如果两个张量在某个维度上的长度既不相同也不为1,则无法应用广播机制进行运算。
内存消耗:
虽然广播机制可以简化代码编写并提高计算效率,但它可能会增加内存消耗。因为在进行广播时,通常需要复制一些元素以扩展张量的形状。
性能优化:
在某些情况下,可以通过避免不必要的广播操作来优化性能。例如,如果可以通过调整张量的形状来避免广播,则应该优先考虑这种方法。
综上所述,向量运算的广播机制是一种强大的技术,它允许我们在处理不同形状的张量时进行逐元素的算术运算。通过理解广播机制的基本原理和规则,我们可以更好地利用这一技术来简化代码编写并提高计算效率。
a为向量 a+1就会触发广播机制 |
|
|
|
|
numpy 数组切片



array([:])切片取值 array([开始索引: 结束索引(不包含本身) : 步长]) import numpy as np x=np.array([1,2,3,4,5,6,7,8,9,10,11,12]) print(x[1:5])#打印index为1~5的数组,范围是左闭右开 [2 3 4 5] print(x[3:])#打印index=3之后的数组,包含index=3 [ 4 5 6 7 8 9 10 11 12] print(x[:9])#打印index=9之前的数组,不包含index=9 [1 2 3 4 5 6 7 8 9] print(x[1:-2])#打印index=1到倒数第2个index之间的数组 [ 2 3 4 5 6 7 8 9 10] print(x[-9:-2])#打印倒数第9个index和倒数第2个index之间的数组,左开右闭 [ 4 5 6 7 8 9 10] array([::]) 间隔与反向 print(x[1::3])#以index=1为起始位置,步长3 [ 2 5 8 11] print(x[::3])#默认从index=0开始,步长3 [ 1 4 7 10] print(x[3::])#和[3:]一样 [ 4 5 6 7 8 9 10 11 12] print(x[::-1])#反向打印数据,从最后一个index开始,步长为1 [12 11 10 9 8 7 6 5 4 3 2 1] print(x[::-3])#反向打印数据,从最后一个index开始,步长为3 [12 9 6 3] print(x[7:2:-1])#反向打印index=2(不包含)到index=7之间的数据 [8 7 6 5 4]
import numpy as np
a=np.random.random((2,3))
a
array([[0.93525862, 0.29607095, 0.37812667],
[0.86951447, 0.08706658, 0.04188698]])
a[:,::2]
array([[0.93525862, 0.37812667],
[0.86951447, 0.04188698]])
默认步长为1
a[::,::2]
array([[0.93525862, 0.37812667],
[0.86951447, 0.04188698]])
[开始索引:截至但不包括在内的索引:步长] |
在科学计算,代码编程的领域中, [3,5,7,2,1,0] 这样多个数组成的列表是1维数据,或者数据的维度是1维 [[3,5,7], [2,1,0]] 像这种有列有行的数据,是2维的, 比如常见的关系数据库中的表,一个表多个列名,可以存多行数据,这样的数据是2维的 import numpy as np data = np.array([3,5,7,2,1,0]) data.ndim #1 data = np.array([[3,5,7],[2,1,0]]) data.ndim # 2 图片的尺寸通常表示 高*宽,即[H,W] 如果有batch_size张图片,可以表示为[B,H,W] 实际上在编程,即数字化的世界中, 用坐标系表示可视化图形时,左上角的点为原点 -------------> 宽 | 3 5 7 | 2 1 0 | | 高 |
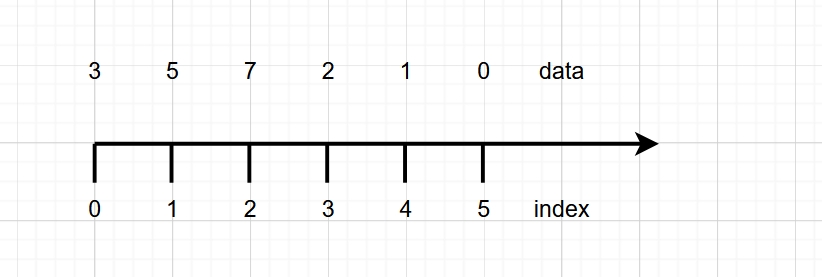
用直线表示数轴 数轴有刻度,标记,后来叫下标,就是一条直线下面的小短线 再后来叫索引 切片就是根据索引取的, [开始索引:截至但不包括在内的索引:步长] 数轴上取的切片为1维数据,或者说单个的数轴可以表示1维数据 平面是2维的,就用两个数轴表示, 现在有两个维度,就得区分出来一个先后,谁为1,谁为2 参考1维数轴,索引是从0开始的,那么 index=0的为第1维, index=1的为第2维 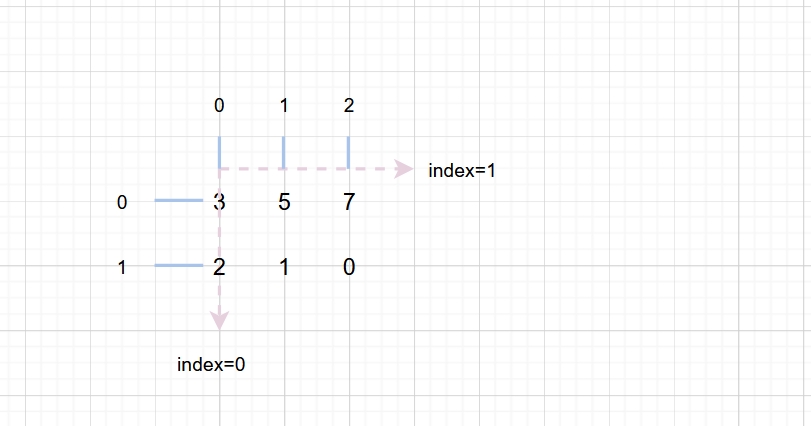
在视觉领域中,比如图片的尺寸为 高*宽, 先列后行 在向量定义中,向量默认为列向量,即视觉上是垂直方向 2维数据就是2维矩阵,是由多个向量组成的,因此, 第1维是垂直方向,第2维为水平方向,这样的定义/规范与很多现象不谋而合 每个维度都可以看作一个数轴,可以进行切片操作, 比如,取第2列数据,就是a[:,1] |
在处理数据时,经常会将一个函数作为一个参数传入一个方法 import numpy as np np.random.seed(73) res=np.random.randint(low=0,high=10,size=(7)).tolist() res.count(4) list有一个count方法,作为参数传入另外一个方法 max(res,key=res.count) 1 res [1, 3, 5, 6, 4, 1, 8] |
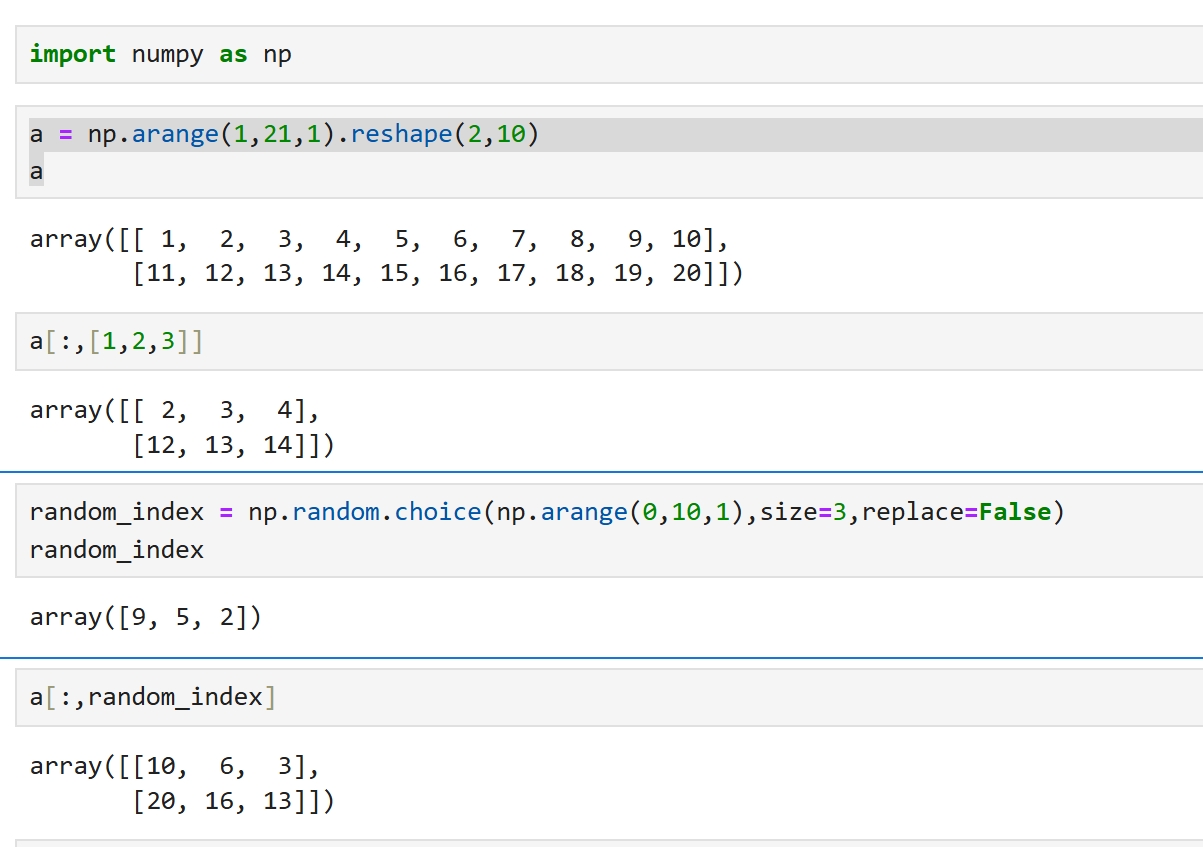
鲁棒性 在AI中,随机抽取特征列的目的在于让算法变得健壮 使用全部的列,未必就是最好的, 最完美的特征是不重不漏, 但现实中提取的特征有着大量的重复,还有遗漏,是即重又漏 另外,还有一些特征实际上是噪声,以为它有用,实际上它是多余的 这时,提取90%的特征,有可能漏选重要特征,也有可能漏选噪声 如果多选一些,就是暴力计算,那么必定有些选择效果好,有些效果差 如此,哪些特征是效果好的,哪些特征效果是差的,就能稍微区分一些了 这个思想极其重要! |
基本运算
线性代数是研究向量、向量空间(也叫线性空间)、线性变换和矩阵等概念的数学分支。在线性代数中,运算的划分并不仅仅基于是否超出原空间这一维度,但理解你提到的这一视角有助于深入探讨其运算特性。以下是从不同角度对线性代数中的运算进行的分类和解释:
一、基于运算对象的分类
向量运算:
加法:两个向量相加得到一个新的向量。
数乘:一个向量乘以一个标量(实数)得到一个新的向量。
内积(点积):两个向量对应元素相乘后求和,结果是一个标量。它表示两个向量在方向上的相似程度或夹角。
外积(叉积):仅适用于三维向量,结果是一个向量,垂直于原两个向量所构成的平面。
矩阵运算:
加法:两个矩阵对应元素相加得到一个新的矩阵。
数乘:一个矩阵的每个元素乘以一个标量得到一个新的矩阵。
乘法:两个矩阵相乘(按行乘列的规则)得到一个新的矩阵。这是线性代数中最重要的运算之一,广泛应用于解线性方程组、计算特征值和特征向量等。
逆运算:求一个矩阵的逆矩阵(如果存在),使得原矩阵与逆矩阵相乘等于单位矩阵。
二、基于运算性质的分类
线性运算:
线性运算满足加法和数乘的封闭性、结合律、交换律和分配律。在线性代数中,向量和矩阵的加法和数乘都是线性运算。
非线性运算:
不满足上述线性运算性质的运算都可以视为非线性运算。例如,矩阵的乘法虽然本身是线性的(因为它是按行乘列的规则进行的),但将两个矩阵相乘看作一个整体对另一个矩阵的运算时,它可能表现出非线性特性(如矩阵乘法的不可交换性)。
按是否超出原空间划分:
封闭运算:运算结果仍在原空间内的运算。例如,向量空间的加法和数乘都是封闭的,因为运算结果仍然是向量空间的元素。
非封闭运算:运算结果超出原空间范围的运算。例如,在某些情况下,矩阵的乘法可能导致结果矩阵的阶数(行数或列数)与原矩阵不同,从而超出原矩阵空间。但需要注意的是,这种划分并不是绝对的,因为它取决于具体的运算定义和上下文环境。
三、其他重要运算 特征值和特征向量: 通过求解特征方程,可以得到矩阵的特征值和对应的特征向量。 它们描述了线性变换对空间的影响。 正交化和正交归一化: 将一组非正交向量转换为正交向量的过程。 这在信号处理、图像处理等领域有广泛应用。 奇异值分解(SVD): 一种常用的矩阵分解方法,可以将一个矩阵分解为三个矩阵的乘积。 SVD在数据降维、信号处理等领域有重要应用。 主成分分析(PCA): 一种基于线性代数的数据降维方法, 通过将数据投影到一个新的坐标系来减少数据的维度。 PCA在数据挖掘、机器学习等领域有广泛应用。 综上所述,线性代数中的运算可以从多个角度进行分类和划分。 这些运算在数学、物理学、工程学等领域都有广泛的应用和重要的意义。 |
import numpy as np a1 = np.array([3,5,7]) a2 = np.array([2,1,0]) a1+a2,a1-a2,a1*a2 (array([5, 6, 7]), array([1, 4, 7]), array([6, 5, 0])) a1/a2 RuntimeWarning: divide by zero encountered in divide a1/a2 array([1.5, 5. , inf]) |
a1@a2 11
import numpy as np
def vec_inner_product(a1,a2):
"""向量内积运算
a1:1维np.array或任何可以转为1维np.array类型的数据,比如list
a2:1维有序数组
"""
if type(a1) is not np.ndarray:
a1 = np.array(a1)
if type(a2) is not np.ndarray:
a2 = np.array(a2)
if a1.ndim==a2.ndim==1:
return (a1*a2).sum()
else:
raise Exception(f"数据维度必须为1维,而实际a1维度为{a1.ndim},a2维度为{a2.ndim}")
a1=[1,1,1] vec_inner_product(a1,a1) 3 在学术中是注重区分一个向量是列向量还是行向量的, 但在工程计算中,不区分这个,重在怎么方便计算 在工程计算中,不管是行向量还是列向量,都是数组/列表 ----------------------------------------------------------- |
linear algebra 英/ˈlɪniə(r) ˈældʒɪbrə/ 美/ˈlɪniər ˈældʒɪbrə/ 线性代数 
import numpy as np a1 = np.array([3,4]) np.linalg.norm(a1) 5.0 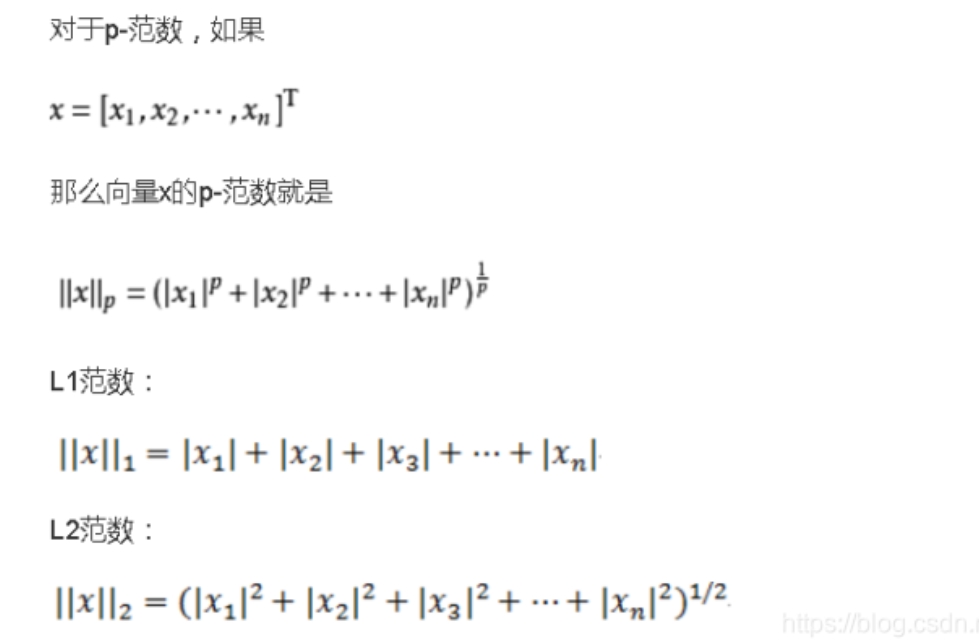
|
|
余弦相似度 求向量(3,4)与向量(4,3)的余弦相似度
import matplotlib.pyplot as plt
import numpy as np
# 定义向量的坐标
vector1 = np.array([3, 4])
vector2 = np.array([4, 3])
# 创建一个新的图形
fig, ax = plt.subplots()
# 设置原点
origin = np.array([0, 0])
# 绘制向量
ax.arrow(origin[0], origin[1], vector1[0], vector1[1], head_width=0.5, head_length=0.7, color='blue', label='Vector 1 (3, 4)')
ax.arrow(origin[0], origin[1], vector2[0], vector2[1], head_width=0.5, head_length=0.7, color='red', label='Vector 2 (4, 3)')
# 添加图例
ax.legend()
# 设置坐标轴标签
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
# 设置坐标轴范围
ax.set_xlim(-1, 8)
ax.set_ylim(-1, 8)
# 添加网格
ax.grid(True)
# 显示图形
plt.show()
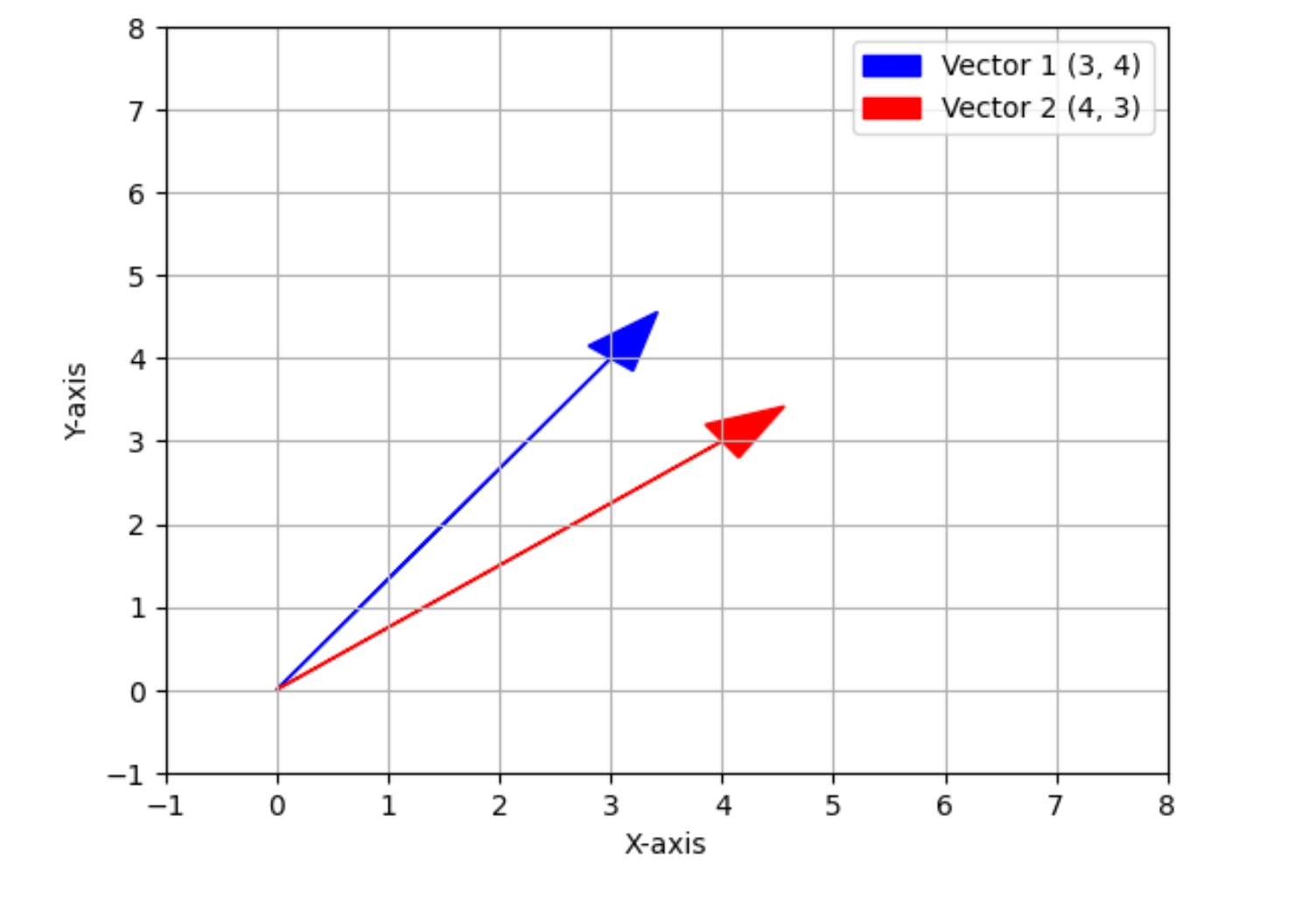
import numpy as np a1 = np.array([3,4]) a2 = np.array([4,3]) a1@a2/np.linalg.norm(a1)/np.linalg.norm(a2) #0.96 0.96从相似度的角度讲,就是96% 相似,接近,重叠,一样... 余弦相似度 是向量内积的归一化,内积除以两个向量的模 是单位向量(模为1)的内积 以夹角反映两个向量的接近程度 |
|
归一化 余弦相似度 不只是重要的,而且还是伟大的,其中一个重要的因素就是 归一化 这里讲的归一化是因为前面涉及到余弦相似度顺带说归一化的,不是专门讲归一化的 单位向量的内积,就是余弦相似度,单位向量就是向量除以其模 模就是距离,长度,差异 在AI中求距离,通常是为了求差异, 两个向量之间的距离,可以衡量两个向量之间的差异,比如距离为0就没有差异 但它们又不完全相同,又加上计算机擅长计算小于1的数的乘法,不容易发生数据爆炸 因为若是一堆大于1的数相乘,数据很容易变得无法计算 所以经常对数据做归一化,使数据在1附近, 经典的是标准正态分布:数据之间的平均距离为1,标准差std=1 这样向量的模型就近似于1,四舍五入为1,或者在1附近 归一化计算
import numpy as np
def layer_norm(x, epsilon=1e-5):
"""
对输入张量x进行层归一化。
参数:
x (numpy.ndarray): 输入张量,形状为 (batch_size, num_neurons) 或 (num_neurons,)
epsilon (float): 防止除以零的小数,默认为1e-5
返回:
numpy.ndarray: 归一化后的张量,与输入x形状相同
"""
# 确保x是二维数组,即使只有一个样本
if x.ndim == 1:
x = x.reshape(1, -1)
# 计算均值和标准差,axis=1表示沿着神经元维度计算
mean = np.mean(x, axis=1, keepdims=True)
std = np.std(x, axis=1, keepdims=True)
# 归一化
x_normalized = (x - mean) / (std + epsilon)
# 注意:在实际应用中,通常会引入可学习的参数gamma和beta
# 这里为了简单起见,我们不使用这些参数
return x_normalized
归一化一个极其重要 但少有人提及的功能 是它能将 同维度向量的模 拉到 一个非常相似的值 附近
for i in range(10):
a1=np.random.randint(low=-10,high=100,size=(3,7))
print(np.linalg.norm(layer_norm(a1)))
4.582573754587523
4.582573309139827
4.58257333877472
4.582573767640809
4.582574281779658
4.582572798176719
4.58257428062735
4.582574118227493
4.582574038333116
4.582573448513566
for i in range(10):
a1=np.random.randn(3,7)
print(np.linalg.norm(layer_norm(a1)))
4.5825084359593715
4.582518737338171
4.582514514444213
4.582508795192072
4.582521019590121
4.582499865252969
4.582532528847727
4.582527187577756
4.5824889626794185
4.582513339038036
for i in range(10):
a1=np.random.randn(3,10)
print(np.linalg.norm(layer_norm(a1)))
5.477165901060984
5.477165154254828
5.477153741100626
5.4771733471338715
5.477168639464526
5.477172057459369
5.477168185783753
5.47713605619315
5.47716747851023
5.477174399325082
for i in range(10):
a1=np.random.randn(3,20)
print(np.linalg.norm(layer_norm(a1)))
7.745886973943938
7.745885924748168
7.745892158689112
7.745886100402846
7.745889309726147
7.745866613244086
7.745901945535937
7.745878136185315
7.745887837866451
7.745897892836759
向量同维度的情况下,归一化后其值基本相同,小数点后5位相同,通常AI计算的精度也是5位 这就意味着,在此情况下计算向量内积,就等价于计算余弦相似度, 因为不同向量的分母一样,就是模一样, 余弦相似度是除以向量自己的模,归一化后所有向量的模基本相等, 现在向量之间的差异就可以由内积体现了 在归一化的情况下,向量的模依然随维度的增加而增加 在深度学习中,向量的维度在不断地学习, 同时向量的维度非常高,成千上万,那么有没有一种方法, 可以在向量的维度增加时,向量的模依旧不变的方法 在深度学习中使用的方法是,归一化后,再除以维度的开平方根
import numpy as np
def layer_norm(x, epsilon=1e-5):
"""
对输入张量x进行层归一化。
参数:
x (numpy.ndarray): 输入张量,形状为 (batch_size, num_neurons) 或 (num_neurons,)
epsilon (float): 防止除以零的小数,默认为1e-5
返回:
numpy.ndarray: 归一化后的张量,与输入x形状相同
"""
# 确保x是二维数组,即使只有一个样本
if x.ndim == 1:
x = x.reshape(1, -1)
# 计算均值和标准差,axis=1表示沿着神经元维度计算
mean = np.mean(x, axis=1, keepdims=True)
std = np.std(x, axis=1, keepdims=True)
# 归一化
x_normalized = (x - mean) / (std + epsilon)
# 注意:在实际应用中,通常会引入可学习的参数gamma和beta
# 这里为了简单起见,我们不使用这些参数
return x_normalized
import numpy as np
dim = 1000
for d in range(100,dim,100):
for i in range(10):
a1=np.random.randn(3,d)
l2 = np.linalg.norm(layer_norm(a1))
l2 = np.round(l2/np.sqrt(d),decimals=6)
print("dim=",d,"l2=",l2)
可以看到除以维度的开平方后,向量归一化后的模稳定在了1.732033-1.732034之间,非常稳定 dim= 100 l2= 1.732034 dim= 100 l2= 1.732034 dim= 100 l2= 1.732033 dim= 100 l2= 1.732034 dim= 100 l2= 1.732033 dim= 100 l2= 1.732033 dim= 100 l2= 1.732032 dim= 100 l2= 1.732034 dim= 100 l2= 1.732033 dim= 100 l2= 1.732034 dim= 200 l2= 1.732033 dim= 200 l2= 1.732033 dim= 200 l2= 1.732033 dim= 200 l2= 1.732034 dim= 200 l2= 1.732034 dim= 200 l2= 1.732034 dim= 200 l2= 1.732033 dim= 200 l2= 1.732033 dim= 200 l2= 1.732034 dim= 200 l2= 1.732033 dim= 300 l2= 1.732034 dim= 300 l2= 1.732033 dim= 300 l2= 1.732033 dim= 300 l2= 1.732034 dim= 300 l2= 1.732033 dim= 300 l2= 1.732033 dim= 300 l2= 1.732033 dim= 300 l2= 1.732034 dim= 300 l2= 1.732034 dim= 300 l2= 1.732033 dim= 400 l2= 1.732033 dim= 400 l2= 1.732033 dim= 400 l2= 1.732033 dim= 400 l2= 1.732033 dim= 400 l2= 1.732033 dim= 400 l2= 1.732033 dim= 400 l2= 1.732033 dim= 400 l2= 1.732034 dim= 400 l2= 1.732033 dim= 400 l2= 1.732034 dim= 500 l2= 1.732033 dim= 500 l2= 1.732033 dim= 500 l2= 1.732034 dim= 500 l2= 1.732034 dim= 500 l2= 1.732033 dim= 500 l2= 1.732034 dim= 500 l2= 1.732033 dim= 500 l2= 1.732034 dim= 500 l2= 1.732034 dim= 500 l2= 1.732034 dim= 600 l2= 1.732033 dim= 600 l2= 1.732034 dim= 600 l2= 1.732033 dim= 600 l2= 1.732033 dim= 600 l2= 1.732033 dim= 600 l2= 1.732033 dim= 600 l2= 1.732034 dim= 600 l2= 1.732033 dim= 600 l2= 1.732034 dim= 600 l2= 1.732033 dim= 700 l2= 1.732034 dim= 700 l2= 1.732034 dim= 700 l2= 1.732033 dim= 700 l2= 1.732033 dim= 700 l2= 1.732033 dim= 700 l2= 1.732034 dim= 700 l2= 1.732033 dim= 700 l2= 1.732033 dim= 700 l2= 1.732033 dim= 700 l2= 1.732033 dim= 800 l2= 1.732033 dim= 800 l2= 1.732034 dim= 800 l2= 1.732033 dim= 800 l2= 1.732034 dim= 800 l2= 1.732033 dim= 800 l2= 1.732033 dim= 800 l2= 1.732033 dim= 800 l2= 1.732034 dim= 800 l2= 1.732034 dim= 800 l2= 1.732033 dim= 900 l2= 1.732034 dim= 900 l2= 1.732033 dim= 900 l2= 1.732033 dim= 900 l2= 1.732034 dim= 900 l2= 1.732033 dim= 900 l2= 1.732033 dim= 900 l2= 1.732034 dim= 900 l2= 1.732033 dim= 900 l2= 1.732033 dim= 900 l2= 1.732033 |
层归一化是余弦相似度的 近似 这涉及到AI工程中的一个重要思想:有效的近似 余弦相似度是一个纯数学理论,但在工程落地时,并不是一模一样的照搬,而是灵活运用, 思想相同,方法各异,重在效果 余弦相似度是单位向量的内积, 层归一化没有完全让向量的模归于1,而是做到了同维度向量的模精度为小数点后5位相同, 使用简单的计算实现了近似的效果, 同时是先内积还是先除以模也不重要,重要的是除就可以了 层归一化使用的是余弦相似度的思想, 不同的是,层归一化中有另外一个重要思想, 就是将数据拉到以0为中心,数据间平均距离为1的分布上,也就是标准正态分布 将两者结合起来的的,另外一个求相似度的是 皮尔逊相关系数 
皮尔逊相关系数与归一化都涉及到了 分布的均值,标准差,公式也极其近似, 主要是因为它们的思想近似, 有不同是因为应用的具体场景有所不同 归一化通常是为接下来的运算准备的, 归一化之后数据被拉到标准正态分布, 前面有说可以近似,可以灵活运用,所以有时候还可以是以0.5为中心,标准差为0.5的分布,具体看业务场景 皮尔逊相关系数也减均值了,也除以标准差了,也相乘了 重要是皮尔逊涉及的是两个分布, 而归一化涉及的是一个分布,只处理其中一个分布,为接下来的计算做准备,应用场景有 数据预处理,入模的对数据做一次处理, 机器学习通常是一次训练,而深度学习是N轮次的训练, 所以在深度学习中,基本上每个轮次都会加上一次归一化处理 以上所有思想,都是基于一个前提: AI算法重的是数据的差异,而不是数据本身的大小 这是因为 AI算法的目标最终是分类,数据要变得泾渭分明,才容易把类别分开 所以 任何能够 简单且能够把数据的差异化 显现/放大 的方法 都是可行的 自定义计算
import numpy as np
def pearson_correlation_coefficient(x, y):
# 计算均值
mean_x = np.mean(x)
mean_y = np.mean(y)
# 计算分子部分
numerator = np.sum((x - mean_x) * (y - mean_y))
# 计算分母部分
denominator = np.sqrt(np.sum((x - mean_x)**2) * np.sum((y - mean_y)**2))
# 防止除以零
if denominator == 0:
return 0
# 计算相关系数
r = numerator / denominator
return r
# 示例数据
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 6, 8, 10])
# 计算皮尔逊相关系数
correlation = pearson_correlation_coefficient(x, y)
print("Pearson Correlation Coefficient:", correlation) #1
scipy
from scipy.stats import pearsonr
# 示例数据
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 6, 8, 10])
# 计算皮尔逊相关系数
correlation, _ = pearsonr(x, y)
print("Pearson Correlation Coefficient:", correlation)
皮尔逊相关系数对非线性的兼容能力
现实世界的数据不纯粹,有噪声,受多方因素影响,
下面的函数模拟非线性关系,再添加一些噪声
def func(x,others=None):
# 因为函数中有Log,将小于0的元素统一处理也是一种激活方法
x[x <= 0] = 1
# 使用布尔索引找到所有小于0的元素,并将它们替换为十分之一的大小
arr = x
arr[arr < 0] = arr[arr < 0] * 0.1
y = 0.02*x**3 +np.log(x)-0.01*np.exp(x) + 3*x**2 + arr +np.random.randn(x.shape[0])
if others:
y += others
return y
# 示例数据 x = np.array([1, 2, 3, 4, 5]) y = np.array([2, 4, 6, 8, 10]) x2=func(x) y2=func(y) x2,y2 (array([ 4.32762469, 15.43541951, 33.25105883, 53.38260825, 81.50973392]), array([ 15.26327983, 53.68004041, 115.31274319, 181.99099484,111.77809068]))
# 计算皮尔逊相关系数
correlation = pearson_correlation_coefficient(x2, y2)
print("Pearson Correlation Coefficient:", correlation)
Pearson Correlation Coefficient: 0.7102874651348501 经过非线性处理后,它们的线性相关性 仍然有71%, 这说明皮尔逊相关系统有一定的兼容非线性的能力 |
常用的距离的度量有两种: 欧几里德距离,欧氏距离 余弦相似度,前面的归一化,皮尔逊相关系数等都是如此, 余弦相似度也用到了欧氏距离,但更侧重于夹角, 将距离归于单位距离,就是1, 实际的应用中归于一个相对固定的值,比如所有向量的模都是1.73的话,就不用考虑距离了 如此就可以忽视距离,只看夹角 简单说,常用的距离度量方法有两种, 一种是空间中两个点之间的直线距离,从长度考虑 一个是夹角/角度考虑的 下面描述欧氏距离 几何 在日常生活中,求两个位置之间的距离,找个尺子拉开量一量 这相当于是求1维数轴上的两个点的距离|a-b| 虽然说现实世界是3维空间,但人们看世界是线性的,1维的(并且是离散的) 除了极少数学者,普通人看世界就是这么看,求距离就是这么直来直去 但这只能解决简单的问题,更复杂的问题, 需要先建立一个坐标系,将这两个点用坐标表示,通常坐标的计算求距离 在平面中,(3,0),(0,4)两个点之间的距离 (3-0)*(3-0) + (0-4)*(0-4) = 25 25开平方后为5,这就是勾股定理
import matplotlib.pyplot as plt
import numpy as np
# 定义向量的坐标
vector1 = np.array([3, 4])
vector2 = np.array([4, 3])
# 创建一个新的图形
fig, ax = plt.subplots()
# 设置原点
origin = np.array([0, 0])
# 绘制向量(使用虚线)
ax.arrow(origin[0], origin[1], vector1[0], vector1[1], head_width=0.5, head_length=0.7, color='blue', label='Vector 1 (3, 4)', linestyle='--')
ax.arrow(origin[0], origin[1], vector2[0], vector2[1], head_width=0.5, head_length=0.7, color='red', label='Vector 2 (4, 3)', linestyle='--')
# 在(3,4)点上绘制一条垂直的线
ax.axvline(x=vector1[0], color='green', linestyle='-') # 垂直线
# 在(4,3)点上绘制一条水平的线
ax.axhline(y=vector2[1], color='green', linestyle='-') # 水平线
# 在(3,4)和(4,3)之间绘制一条线段
ax.plot([vector1[0], vector2[0]], [vector1[1], vector2[1]], color='black', linestyle='-') # 黑色实线
# 添加图例
ax.legend()
# 设置坐标轴标签
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
# 设置坐标轴范围
ax.set_xlim(-1, 8)
ax.set_ylim(-1, 8)
# 添加网格
ax.grid(True)
# 显示图形
plt.show()
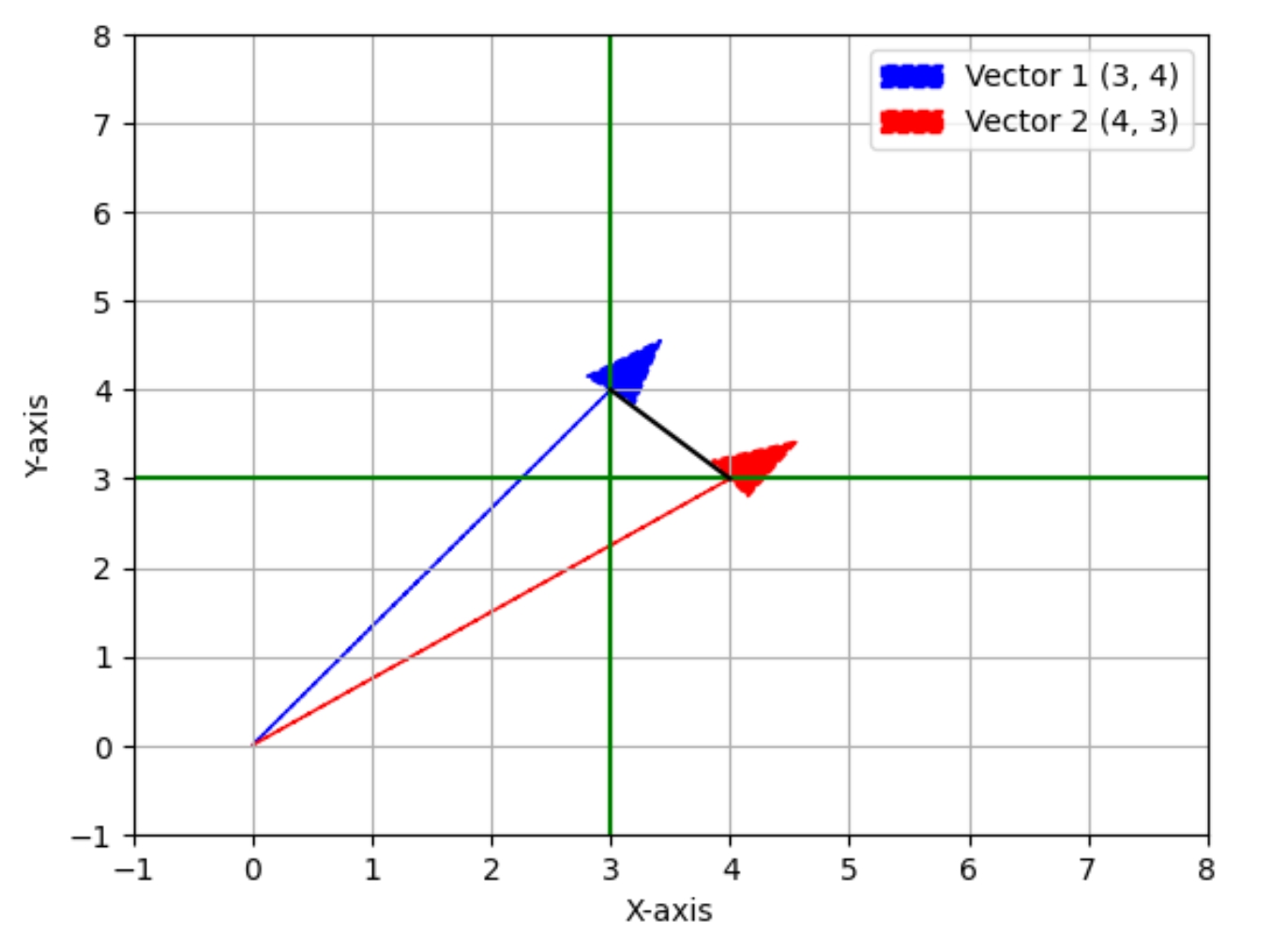
3维依然是各个维度上的元素想减,平方,相加再开方 从2维开始,3,4,...,n维向量的长度计算都是如此,这就是欧氏距离 |
|
坐标系的本质 实际是正交直角坐标系,任何两个维度都是相互垂直的 针对一个复杂事物,构建一个体系,该体系有以下特征 1. 任何一个维度都没有其他维度上的事物,正交,几何上表现为垂直,含义为在其他维度上投影的长度为0,简单说就是 不重 2. 所有维度综合起来能完全表示所要表示的事物,不会遗漏任何一个部分,简单说就是 不漏 3. 单个维度有两个重要元素:方向,大小,对应定性分析,定量分析两个理论方法 比如,平面为什么用两个相互垂直的数轴表示, 为什么非要垂直 多一个轴方便吗 少一个轴可行吗 这就是一个好用的坐标系的三大要素:不重,不漏,方向和大小
使用(1,0)表示x轴上单位向量,那么(3,0)可表示为3*(1,0)
使用(0,1)表示y轴上单位向量,那么(0,4)可表示为4*(0,1)
平面中的(3,4)点= 3*[1,0] + 4*(0,1)
使用单位矩阵,一列表示一个维度
E=
[[1,0],
[0,1]]
平面上的点(3,4)是2维的,用2维矩阵进行表示
E@[3,4] = [[3,0],
[0,4]]
[3,0]又可以表示为3*[1,0],表示在[1,0]维度上的特征值为3
如此,
2维空间即平面中所有点都可以用2维矩阵表示,
2维空间即平面内的所有计算全部转化为2维矩阵之间的计算
同样可扩展至n维空间
向量的特征/元素 与 坐标系表示 向量 有一一对应的关系
在AI中,构建数据的特征时,最完美的特征,就是这样不重不漏的特征,
用这样的特征表示一个样本/事物,与将事物在坐标系中分解表示是等价的
从2维开始,第3,4,...,n维的计算都是一样的, 为什么不从第1维开始? 第2维3*(1,0),(1,0)单位向量表示了一个方向 要想有方向,至少需要两个事物,a相对b, 现实中的方向更是复杂,是N多事物相对方向,或者说是3维空间的方向, 如果是单一的事物,比如,一个数粙,横着竖着都是一样的,是没有方向的,只有距离 距离单个事物就可以,比如单维数轴上的两个点,|a-b|就可以 而方向,其实就是夹角,至少需要两个边的,单边,比如单个数轴形不成夹角, 即,方向本身就是至少2维空间才有的概念 所以1维上,只有大小,没有方向, 把一条直接看成两条重合的,或者以中间某个点断成两个射线,都是创造两个边,既然如此,为啥不是n个重叠,断开n段... 不符合坐标系的设计理念 从第2维开始,都是从大小,方向两个要素描述一个维度的,所以它们的计算方式一样 坐标系可以将一个复杂事物分解为简单的事物 通过简单事物的 线性组合 去表示一个复杂事物 简单到什么程度,简单到单一维度,只有方向与大小两个要素 线性组合,就是线性表示,其运算相对乘法,阶乘,冥运算等也是简单的 在更底层的维度上反而取得了更高的计算效率,进而解决了原层面比较难以解决的复杂问题 也是因为人们看世界就是线性的, 或者说线性计算是人本能地就能从事的计算,所以老想着找一些符合人特点的计算方式 其他生命本能看世界的方式与人就不同,它们的计算方法大概率与人是不一样的 简言之,坐标系就是构建一个体系,在该体系中,把复杂事物分解到线性维度进行计算 本部分仅个人理解,如有雷同纯属巧合,如有其他想法,实属正常... |
坐标系首先构建一个体系,这就是首先划分要分析事物的全体及边界,即范围 在AI中, 首先要确定的是全体数据集,这与坐标系是同理的,先划定范围,集合 之后所有的分析处理,都在这个集合/空间中 比如,下面表示两个样本,有三列 [10, 1, 0.1], [20, 2, 0.2] 列1 [10,20], 列2 [1,2], 列3 [0.1,0.2] AI中 第1目标是分类,就区分差异, 第2目标是好算,计算机更擅长计算[0,1]之间的数 所以,在模型计算之前,可以对数据做下面的预处理 [10,20]/100 = [0.1,0.2] [1,2]/10 = [0.1,0.2] [0.1,0.2]/1 = [0.1,0.2] 这就是归一化,统一量纲,将所有样本的模拉到一个固定的值附近 剩下的就是内部之间的差异 列维度归一化之后,全体数据集的数据都在相对集中的一个区域, 之后还有 层归一化-单个样本的维度 批归一化-全体样本的维度 这些归一化都在努力将距离维持在一个固定的范围, 然后差异转化为样本内部之间的差异, 样本的模同差不多,样本内部元素的差异越大就越能体现出不同 |
不谋全局者,不足以谋一域 AI就是先去学习一个事物的全体,然后再去预测相似的个体 先去掌握一类事物的规律,再看其中某个对象 这就相当于一个人把一个领域中的知识,掌握了七七八八之后, 再去解决其中某个问题,就简单多了 反过来,如果是一个样本预测的效果不好,那必定是所学有缺 1. 数据有缺,并不是全体, 比如屋里养了一株喜阳植物,你天天上班忙的不得了,没空浇水, 它缺光又缺水,自然是长不好的 2. 算法有缺,针对当前的数据,算法没学到位; 还是那个植物,它本喜欢疏松的弱本性土壤, 结果你那土壤因时间长变成坚硬的碱性土壤了,你不自知... 所以,做成一件事,有两大前提: 1. 集齐所有的数据 2. 掌握其中规律 如果没做成,就要反思,是数据不全,还是没学到位? 现在有大量的人在教人如何去掌握规律,但这是有前提的, 如果你没有那些数据,学了这些规律也没用,只是在浪费时间, 因为这些规律涉及的使用场景、资源,是一个普通人这辈子都接触不到的... 从数据中学规律,学完规律,还是要去处理数据的... AI做事,从来不会 只关注个体,只关注细节,只关注鸡毛蒜皮的小事... AI准确率90%, 预测的时候,针对某个体不一定准确, 但针对1000个个体,可以确定有900个左右是准确的 |
AI从数据中学习规律,数据有什么规律就学习什么规律 一个规律不在这些数据中,AI是学不到的;如果学到了,那么必定是数据中有这个规律 |
numpy 排序
数组排序
import numpy as np np.random.seed(73) a=np.random.randint(low=1,high=10,size=5) print(a) # [7 3 1 9 4] a.sort() print(a) # [1 3 4 7 9]
argsort索引排序
import numpy as np a=np.arange(start=2,stop=-1,step=-1) print(a) # array([2, 1, 0]) # 索引排序,默认按值的升序排列 print(a.argsort()) # array([2, 1, 0]) print(a[[2, 1, 0]]) # array([0, 1, 2])
二维矩阵
|
看一个矩阵要先列后行 一个纯数据的矩阵,尤其是AI中的二维矩阵, 列是第1维, index=0,代表一个特征,类似二维关系数据表中的一列,比如,名称,年龄 行是第2维,index=1,代表一个样本,类似二维关系数据表中的一行,比如,张三,李四 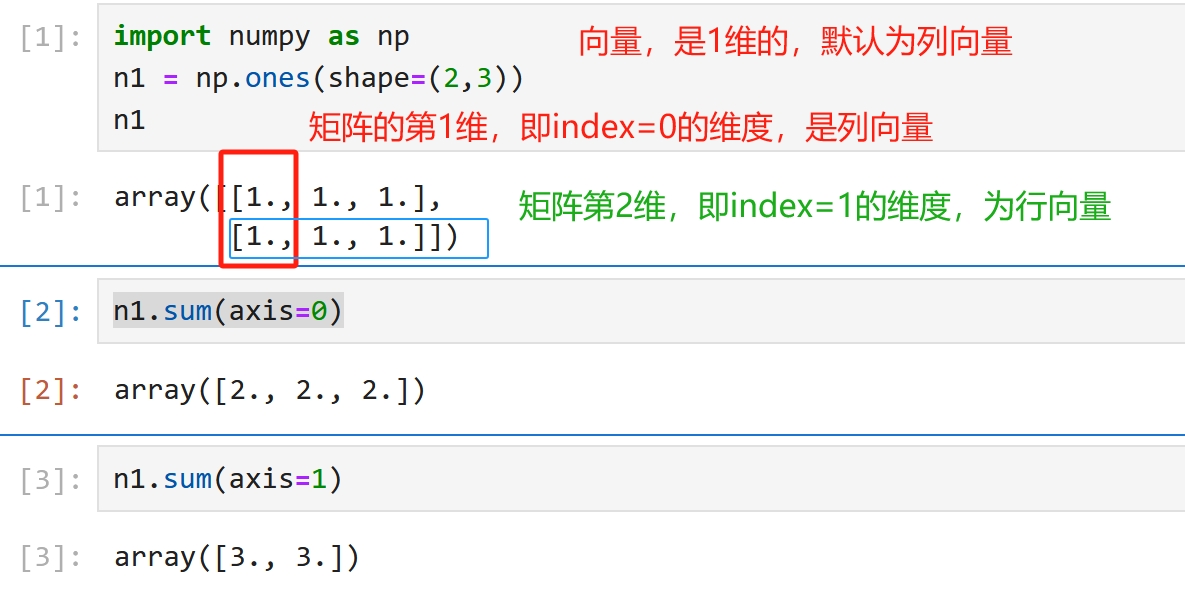
|
import numpy as np n1 = np.ones(shape=(2,3)) shape=(2,3)表示 2行3列 数多少行,是按列的方向数的,因此 2 在index=0,第1个维度上 更专业的讲法为,第1维有2个数据,第2维为3个数据 矩阵运算 矩阵A(aij)与矩阵B(bij) 加减乘除,行对行,列对列,是各自对应元素aij与bij的加减乘除,矩阵shape不变,这就要求AB同shape 内积,是A的行向量与B的列向量进行内积运算, 是A行对B列,通常改变矩阵shape |
import numpy as np
B1 = np.array([
[1,1,1],
[2,2,2]])
B2 = np.array([
[1,2],
[1,2],
[1,2]])
def matrix_mul(B1, B2):
print(np.matmul(B1,B2))
print(np.dot(B1,B2))
print(B1@B2)
matrix_mul(B1, B2)
"""
[[ 3 6]
[ 6 12]]
[[ 3 6]
[ 6 12]]
[[ 3 6]
[ 6 12]]
"""
B1 = np.array([
[1,2,1],
[1,1,2]])
B2 = np.array([
[1,2],
[1,2],
[1,1]])
matrix_mul(B1, B2)
"""
[[4 7]
[4 6]]
[[4 7]
[4 6]]
[[4 7]
[4 6]]
"""
-------------------------------------------------------- |
A@B 矩阵A 与矩阵B 矩阵B 是对矩阵A 行维度的变换,将行从一个维度变换到另外一个维度 矩阵A 是对矩阵B 列维度的变换,将列从一个维度变换到另外一个维度 从纯数学的角度看,二者没有任何的区别, 这二者是看矩阵乘法的两个视角,如同盲人摸象,不同的人摸的是不同的位置,大象还是那个大象 同时,也不只是仅这两个视角,还是第三个,就是不去区分什么列与行维度之分, 而将矩阵A与矩阵B视为一个整体,矩阵所有元素同时相互作用,所有的结果同时诞生 第三种则是自然界的规律,根本没有什么列与行,所有事情的发生,是同时进行的 在线性代数工程数学中,通常会说 Ax = λx ,参数在左,变量在右 AI工程场景,对数据的处理,通常是一行一个样本,数据使用字母x表示,参数为W 一行数据对应一个输出结果,不管过程如何,一定是一个样本输出一个结果, 这个结果可以是一个数,也可以是一个向量 一行数据多个维度,要对行的维度进行变换 下面就从AI工程的场景出发,自定义矩阵乘法
import numpy as np
def vec_inner_product(a1,a2):
"""向量内积运算
a1:1维np.array或任何可以转为1维np.array类型的数据,比如list
a2:1维有序数组
"""
if type(a1) is not np.ndarray:
a1 = np.array(a1)
if type(a2) is not np.ndarray:
a2 = np.array(a2)
if a1.ndim==a2.ndim==1:
return (a1*a2).sum()
else:
raise Exception(f"数据维度必须为1维,而实际a1维度为{a1.ndim},a2维度为{a2.ndim}")
def matrix_product(m1,m2):
"""矩阵乘法
"""
if type(m1) is not np.ndarray:
m1 = np.array(m1)
if type(m2) is not np.ndarray:
m2 = np.array(m2)
if not m1.ndim==m2.ndim==2:
raise Exception(f"数据维度必须为2维,而实际m1维度为{m1.ndim},m2维度为{m2.ndim}")
#这里从右矩阵对左矩阵中行维度变换的角度出发
col_num = m2.shape[1]
row_num = m1.shape[0]
res = np.zeros((row_num,col_num))
for c in range(col_num):
for r in range(row_num):
a1 = m1[r,:].reshape(-1)
a2 = m2[:,c].reshape(-1)
res[r,c] = vec_inner_product(a1,a2)
return res
aa = np.ones((2,3))
bb = np.ones((3,2))
matrix_product(aa,bb)
array([[3., 3.],
[3., 3.]])
aa@bb
array([[3., 3.],
[3., 3.]])
矩阵相乘就是线性变换 线性变换是一种方法,它的目的是变换事物的维度,从一个维度到另外一个维度 比如,分类问题,就是将一个多维的样本,归于一维的类别 |
|
|
二维矩阵·矩阵分解
|
相乘是交融 矩阵A@矩阵B = 矩阵C 矩阵乘法是两个矩阵变为一个矩阵,是线性变换,是两个事物的 “交融” 新生矩阵C 具有 左矩阵A的行维度,又具有右矩阵B的列维度 有交融,那有没有分解? 矩阵A@矩阵B 可以到 矩阵C ,那矩阵C 能否 逆向 到 矩阵A@矩阵B 由于“矩阵A@矩阵B = 矩阵C ”连接左右是的等号“=”,表示的是两者完全等价, 左边可以=右边,右边必然也是可以等左边的, 因此这个结果是必然,关键是如何做? |
矩阵由向量组成,研究矩阵分解,可以先研究其基本组成-向量的合成与分解 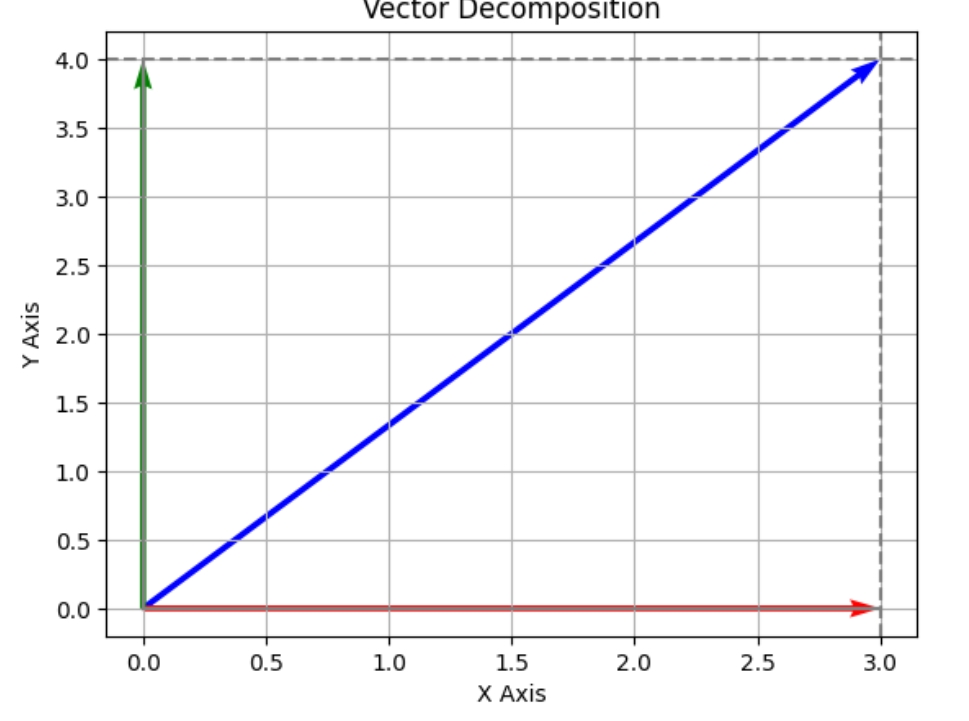
在解析几何中,向量可以分解到坐标系,或者说任何一个向量都可以使用2维平面直角坐标系进行“表示” 注意是“表示”,不是等号= ,这里的表示,指作用效果相同, 这个“作用效果”类似于力的合成与分解,就是物理中的那个无比伟大的概念-“力” 这个力与向量可以一一对应,这个力可以分解 一个力可以 等效于/分解为 无数个力的相互作用, 但最最最 简洁的还是,分解到 “平面”“直角”坐标系的这种场景,就是正交分解 就是“一变二”,且 “正交” - 只要能一变二,那必然就能一变无数 - 正交是所有角度中最特殊的,最简洁,最能满足不重不漏,就是线性代数中“线性无关”且“满秩”思想的 
单从长度/距离的角度看 5*(3/5) = 3 对应向量投影到x轴,描述了长度的变换 向量与数的区别在哪里? 5这里代表的向量的长度,那么我们更想代表的是这个向量 先看数轴 3 是x轴上的一个点,用向量去表示就是(3,0), x轴之所以叫x轴,更重要的意义,是表示一个方向,这里使用单位向量(1,0)描述 那么就有(3,0) = 3*(1,0) 这就完成了一个向量在坐标系中的描述,数值λ*向量x x轴,y轴更多的是表示方向,x轴方向可以由向量(1,0)表示,y轴方向可以由向量(0,1)表示 向量投影到x轴(方向),(3,4)@(1,0) = 3(1,0) 向量投影到y轴(方向),(3,4)@(0,1) = 4(0,1) 抽象一下,向量a 投影到向量x的方向可以表示为 a@x = λx ,简记为ax = λx 还原: 当λ=3时,x=(1,0) 当λ=4时,x=(0,1) 画图代码如下
import matplotlib.pyplot as plt
import numpy as np
# 定义向量的坐标
vector_x = 3
vector_y = 4
vector_length = np.sqrt(vector_x**2 + vector_y**2) # 计算向量长度
# 创建图形和坐标轴
fig, ax = plt.subplots()
# 绘制向量
ax.quiver(0, 0, vector_x, vector_y, angles='xy', scale_units='xy', scale=1, color='b')
# 绘制x轴和y轴上的分解向量
ax.quiver(0, 0, vector_x, 0, angles='xy', scale_units='xy', scale=1, color='r')
ax.quiver(0, 0, 0, vector_y, angles='xy', scale_units='xy', scale=1, color='g')
# 绘制从(3,4)到x轴的垂直虚线
ax.axvline(x=vector_x, color='gray', linestyle='--')
# 绘制从(3,4)到y轴的垂直虚线
ax.axhline(y=vector_y, color='gray', linestyle='--')
# 绘制连接点(3,0)和(0,4)的线段
ax.plot([0, vector_x], [0, 0], color='gray')
ax.plot([0, 0], [0, vector_y], color='gray')
# 设置坐标轴标签和标题
ax.set_xlabel('X Axis')
ax.set_ylabel('Y Axis')
ax.set_title('Vector Decomposition')
# 设置网格
ax.grid(True)
# 显示图形
plt.show()
|
在线性代数工程数学中,有这么一个公式 Ax = λx A是一个n*n的方阵,x为向量,即1维矩阵,此处称为 特征向量, λ为一个数值,这里称为 特征值 前面向量的合成与分解中,也有类似的公式ax=λx,与这所描述的意思是一个意思 就是, 一个向量/矩阵 经过一个向量的线性变换后 可以投影到该向量的方向上 这里,将向量a扩展到了 n*n矩阵,且要求这方阵是满秩矩阵,即其行列式不为0 如此之后,在复数范围内必有解,实数范围内不一定 x/x的模 = 单位向量e ,上面的公式就转换为 Ae = λe 之前用于表示x轴方向的(1,0)就是一个单位向量,其模为1, 只是单位向量不一定非得是1,只是所有元素的平方和为1即可 由此可见,x不是固定的某个向量,而是一组通解,表示的是方向,某个维度的方向! 单位向量(1,0),(0,1)是2维空间的两个基, 一个空间的基,可以用于表示该空间的向量, 同样的一个空间中的向量,可以 投影/线性变换 到基的方向上 Ax = λx 就是在表达这个意思 既然x是通解,有无数个,任意乘以/除以一个实数都是可以的,还乘以λ做什么,λ岂不可以任意取值? 注意看公式两边,都有一个x的,x的任意性不会影响到λ λ是依赖于x的相对结构和矩阵A的“元素大小及结构”, λ没有依赖x的大小,只依赖其结构,对于矩阵A则是大小及结构同时依赖的,尤其是大小 A中所有元素乘以2,那么λ必然也是要翻倍的 x乘以2,λ则是不会有任何的变化 所以,λ是矩阵A在向量x方向上的特征值,特征就是特性,独特的意思 λ是矩阵A在x方向上的数值,且是“唯一”的数值,简称为 “特征值” 
线性代数120页 
线性代数121页 |
|
矩阵的特征值所构成的对角阵,就是该矩阵的其中一个相似矩阵 一个矩阵经过初等行变换以及初等列变换后, 可以得到一个行最简形矩阵,此时这个矩阵每行首元素为1 而由特征值构成的对角阵,则只是主对角线上有元素, 其他位置都是0, 在计算时,非常地 方便,高效,并且计算效果与原矩阵近似 矩阵P的逆矩阵@矩阵A@矩阵P = 矩阵B ,则矩阵A与矩阵B互为相似矩阵 在线性代数中,相似矩阵是一个重要的概念,它描述了两个方阵之间的一种等价关系。 以下是对相似矩阵的详细解释: 一、定义 如果存在一个可逆矩阵P,使得方阵A经过相似变换后变成另一个方阵B, 即P^(-1)AP=B, 那么就称矩阵A和B是相似的。 此时,P被称为矩阵A与B之间的相似变换矩阵。 二、性质 相似矩阵具有许多重要的性质,这些性质在矩阵理论和线性代数中扮演着关键角色: 特征值相同:如果两个矩阵A和B相似,那么A和B的特征值相同。这意味着,无论我们如何通过对角化变换矩阵,其特征值都不会改变。 行列式值相同:相似矩阵的行列式值相同,即det(A)=det(B)。这是因为行列式值等于矩阵特征值的乘积,由于相似矩阵的特征值相同,所以它们的行列式值也相同。 秩相同:相似矩阵的秩相同,即rank(A)=rank(B)。这是因为矩阵的秩等于其非零特征值的个数,由于相似矩阵的特征值相同,所以它们的秩也相同。 迹相同:相似矩阵的迹相同,即tr(A)=tr(B),其中tr表示矩阵的迹,即对角线元素之和。这是因为迹等于矩阵对角线元素之和,而相似变换不会改变对角线元素之和。 可逆性相同:如果两个矩阵相似,那么它们要么都是可逆的,要么都是不可逆的。这是因为一个矩阵是可逆的当且仅当其行列式值不为零,而相似矩阵的行列式值相同,所以它们的可逆性也相同。 此外,相似矩阵还具有反身性(任何矩阵都与它本身相似)、对称性(如果A和B相似,那么B也和A相似)和传递性(如果A和B相似,B和C相似,那么A和C也相似)等性质。 三、应用 相似矩阵在线性代数和应用数学中有着广泛的应用。 例如,在矩阵对角化、求解线性方程组、分析矩阵的性质等方面,相似矩阵都发挥着重要作用。 通过相似变换,我们可以将复杂矩阵简化为更易于分析的形式,从而更方便地求解相关问题。 综上所述,相似矩阵是线性代数中一个重要的概念,具有广泛的应用和丰富的性质。 理解相似矩阵的概念和性质,对于学习和研究线性代数和应用数学具有重要的意义。 |
奇异值分解(SVD)的本质就是 求方阵的特征值与特征向量 奇异只是一种叫法,实际指特征,就是特征分解的意思 SVD的目的就是求矩阵的由特征值构成的对角阵,也是较为简洁形式的相似矩阵 S就是特征值列表 A = np.arange(12).reshape(3,4) U,S,V = np.linalg.svd(A) U.shape,S.shape,V.shape ((3, 3), (3,), (4, 4))
A = np.array([3,4]).reshape(1,2)
U,S,V = np.linalg.svd(A)
U
array([[-1.]])
S
array([5.])
V
array([[-0.6, -0.8],
[-0.8, 0.6]])
奇异值分解(Singular Value Decomposition, SVD)是线性代数中的一种分解方法, 它可以将一个矩阵分解为三个特殊矩阵的乘积。 SVD 在信号处理、统计学、机器学习等多个领域有着广泛的应用, 尤其是在数据压缩、去噪和特征提取等方面。 
然而,在实际编程中,尤其是在使用 NumPy 库进行 SVD 分解时, 返回的 Σ 矩阵通常以向量形式给出,而不是完整的对角矩阵。 因此,如果你使用 U, S, V = np.linalg.svd(A) 进行 SVD 分解,得到的各部分含义如下: 
使用这种方式,你可以通过 np.diag(S) 将 S 转换为一个对角矩阵,然后手动构造出原始的 SVD 形式: 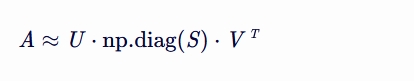
注意,这里的“≈”表示当 A 不是方阵或者其秩小于其行数和列数的最小值时, SVD 分解后的重构可能只是原矩阵的一个近似。 如果 A 是方阵且满秩,那么这种分解是精确的。
理论上最右边乘以的是V的转置矩阵,但numpy实际运算的是乘以V
A = np.array([[2, 9, 4], [3, 5, 7],[8,1,6]])
U,S,V = np.linalg.svd(A)
U@np.diag(S)@V
array([[2., 9., 4.],
[3., 5., 7.],
[8., 1., 6.]])
V_transpose = np.transpose(V)
U@np.diag(S)@V_transpose
array([[ 7.74792398, -2.17307986, 6.02058119],
[ 3.50371068, -4.87357618, 6.85363164],
[ 1.43909048, -9.53015986, 2.84694075]])
矩阵P的逆矩阵@矩阵A@矩阵P = 矩阵B ,则矩阵A与矩阵B互为相似矩阵 那U与V是互为逆矩阵吗? U_inv = np.linalg.inv(U) _,su,_=np.linalg.svd(U_inv) _,sv,_=np.linalg.svd(V) su,sv (array([1., 1., 1.]), array([1., 1., 1.])) 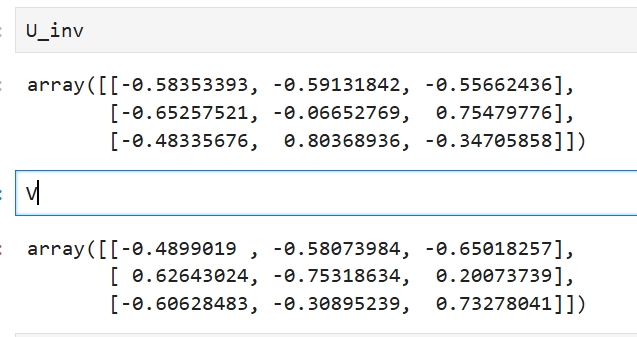
U逆矩阵与V虽然没有完全相等,但其特征对角阵是完全一致的,它们至少是相似矩阵 |
实际上遇到的矩阵都不是方阵 import numpy as np A = np.array([[3, 5, 7], [2, 1, 0]]) U,S,V = np.linalg.svd(A) U.shape,S.shape,V.shape ((2, 2), (2,), (3, 3)) 单看这个结果,是无法进行U@S@V运算的,因为shape对不上 这里需要对矩阵S进行补0,将它的行的维度扩充到V的列维度 S array([9.19356292, 1.86504714])
S = np.hstack((np.diag(S),np.zeros((2,1))))
U@S@V
array([[3.00000000e+00, 5.00000000e+00, 7.00000000e+00],
[2.00000000e+00, 1.00000000e+00, 1.11022302e-16]])
U:左奇异矩阵 S:奇异值,从大到小排序好,最后的数据会接近零 V:右奇异矩阵 SVD的作用是 信息抽取, 比如PCA降维,推荐算法中信息提取,图像中信息提取 from matplotlib import pyplot as plt path="绞股蓝.jpg" img = plt.imread(path) img.shape (369, 616, 3) 
#取中间的绿色 img1 = img[:,:,1] img1.shape (369, 616) plt.imshow(X=img1) 
import numpy as np U,S,V = np.linalg.svd(img1) U.shape,S.shape,V.shape ((369, 369), (369,), (616, 616)) 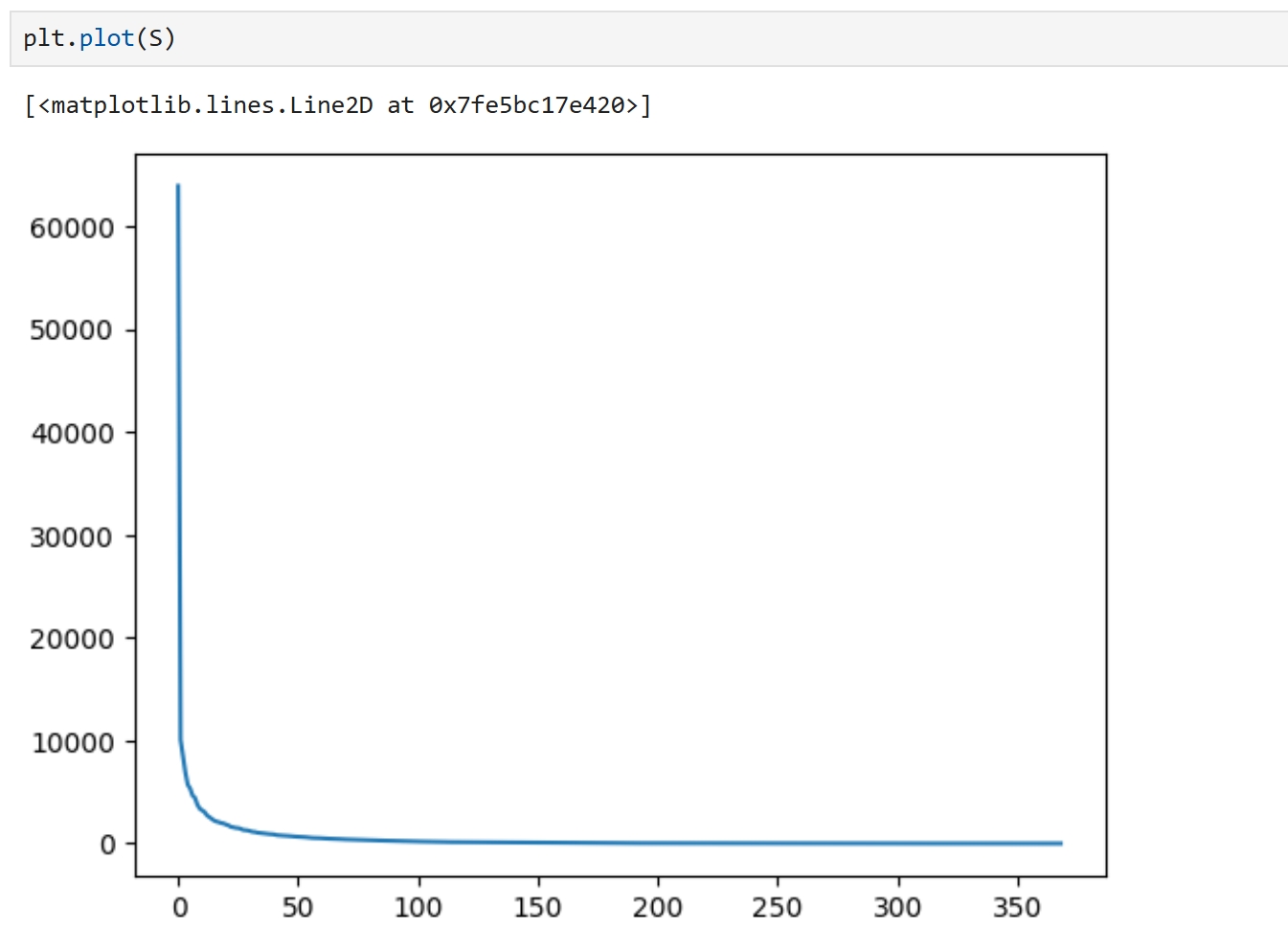
在图像中SVD的值快速地由大变小 SVD奇异值越大,信息价值越大,越重要,越小,越接近0,越不重要... 奇异值重要的部分,代表了事物的主要信息 S的第1个值,与矩阵U的第1行对应,同时与矩阵V的第1行对应 若最重要的n个奇异值,就是S[:n],那么就要取矩阵U的前n列,矩阵V的前n行 由图像可以看出,数据从50开始就开始平衡接近0,那可以取前50个特征值 n=50 img_new = U[:,:n]@np.diag(S[:n])@V[:n,:] plt.imshow(X=img_new) 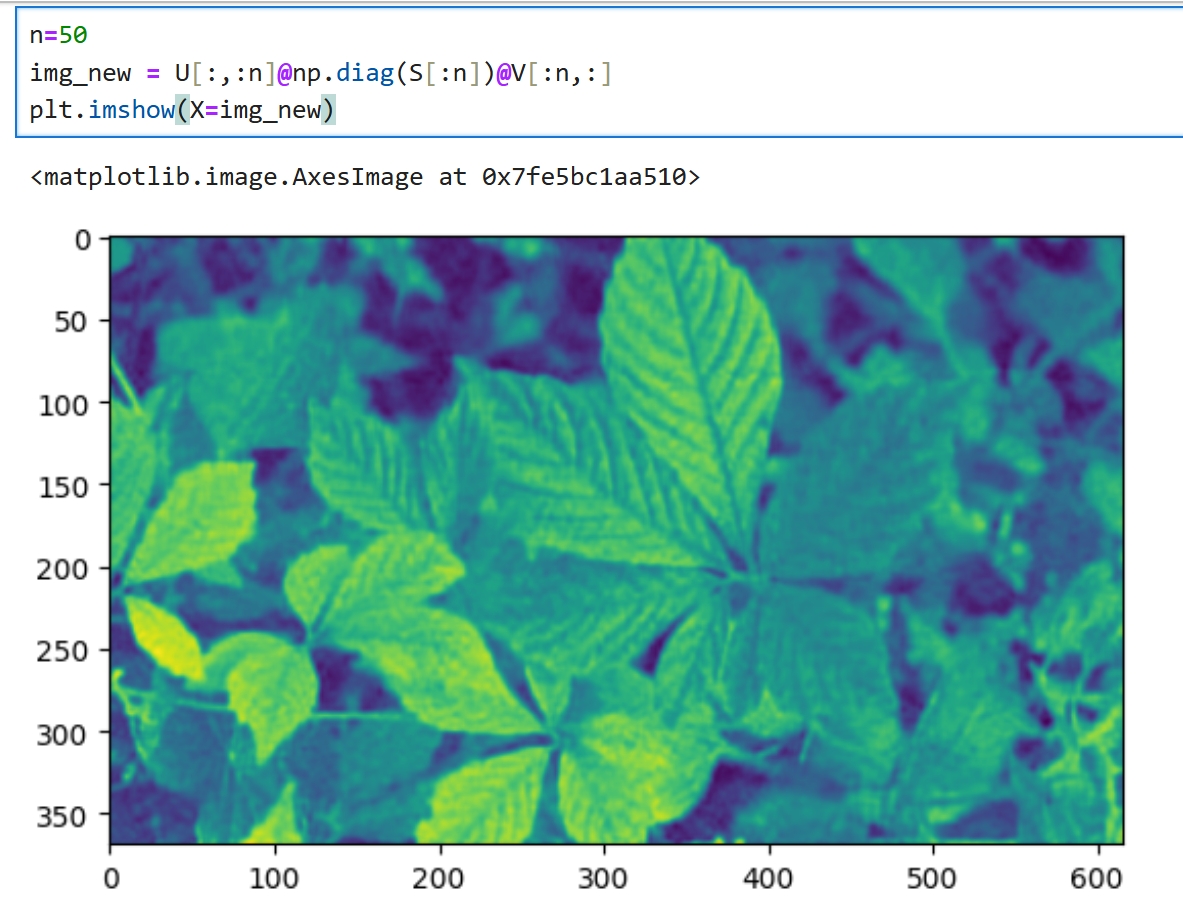
可以看到重新计算的图像,与原图像具有很高的相似度,不细看的话,看不出来什么区别,细看会感觉图像模糊了一些 图像的shape的也没有变化 img_new.shape (369, 616) 只是少了很多不重要的信息,从369个奇异值中取了前50个,信息量下降了一个级别 这就是信息提取 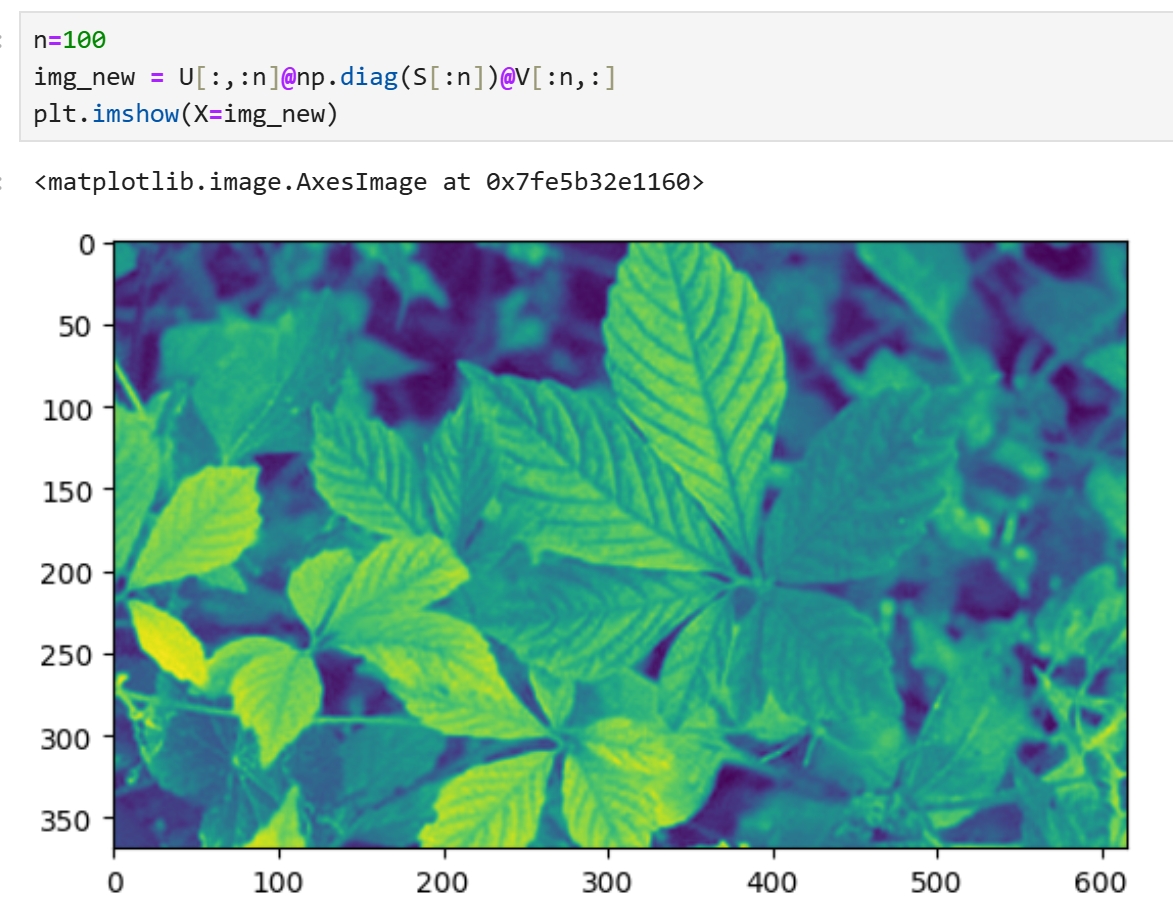
取前100个奇异值,大约三分之一的奇异值,这次就清晰了很多,甚至肉眼无法区分与原图的区别了 |
作为一名机器学习算法工程师,我将结合乳腺癌数据集来详细解释PCA(主成分分析)降维的过程和优势。
一、PCA降维概述
PCA是一种常用的数据降维和特征提取方法,它通过线性变换将高维数据转换为低维数据,从而发现数据中的内在结构和模式。PCA的主要作用包括:
削减数据维度:减少特征的数量,降低数据的复杂性。
去除冗余特征:筛选掉与预测目标不相关的特征,减少噪声的影响。
解决多重共线性问题:将高度相关的特征合并为一个主成分,提高预测模型的稳定性。
突出重要特征:选择保留那些解释数据变异最多的主成分,提高预测的准确性。
二、乳腺癌数据集介绍
乳腺癌数据集通常包含大量患者的临床数据和生物标记物数据,这些数据具有高维度和复杂性的特点。例如,数据集可能包括患者的年龄、肿瘤大小、肿瘤分级、受累淋巴结数量、孕激素受体表达水平、雌激素受体表达水平等多个特征。这些特征之间可能存在相关性,且部分特征对乳腺癌的预测可能并不重要。
三、PCA降维在乳腺癌数据集中的应用
数据预处理:
对原始数据进行去中心化处理,即每个特征的值减去该特征的均值,使得数据的均值为零。
对数据进行标准化处理,即每个特征除以其标准差,使得每个特征的方差为1。
计算协方差矩阵:衡量各个特征之间的相关性。协方差矩阵的对角线上的元素表示各个特征的方差,非对角线上的元素表示不同特征之间的协方差。
特征值分解:对协方差矩阵进行特征值分解,得到特征值和特征向量。特征向量构成了原始数据空间的一组正交基,而特征值代表了在相应特征向量方向上的方差大小。
选择主成分:按照特征值的大小对特征向量进行排序,选取前k个特征向量作为主成分。这些主成分能够最大程度地保留原始数据中的方差信息。
数据投影:将原始数据投影到选取的主成分上,得到降维后的数据表示。
四、PCA降维的优势与效果
提高预测准确性:通过去除冗余特征和解决多重共线性问题,PCA能够提升乳腺癌预测模型的准确性。
简化模型:降维后的数据具有更少的特征,使得预测模型更加简洁和易于理解。
减少计算复杂度:低维数据能够降低模型的训练时间和预测时间,提高计算效率。
可视化数据:PCA可以将高维数据转换为二维或三维表示,有助于直观地观察数据的分布情况和结构特点。
decomposition 英/ˌdiːˌkɒmpəˈzɪʃn/ 美/ˌdiːˌkɑːmpəˈzɪʃn/ n. 分解;腐烂 五、示例代码 以下是一个使用Python和scikit-learn库进行PCA降维的示例代码: python import pandas as pd from sklearn.datasets import load_breast_cancer from sklearn.decomposition import PCA from sklearn.preprocessing import StandardScaler # 加载乳腺癌数据集 data = load_breast_cancer() X = pd.DataFrame(data.data, columns=data.feature_names) y = pd.Series(data.target) # 数据预处理 scaler = StandardScaler() X_scaled = scaler.fit_transform(X) # 使用PCA进行降维 pca = PCA(n_components=2) # 将数据降维到2维 X_pca = pca.fit_transform(X_scaled) # 输出降维后的数据 print(X_pca) 在这个示例中,我们首先将乳腺癌数据集加载到Pandas DataFrame中,并对数据进行标准化处理。然后,我们使用PCA将数据降维到2维,并输出降维后的数据。这样,我们就可以在二维空间中可视化乳腺癌数据,并观察数据的分布情况和结构特点。 综上所述,PCA降维在乳腺癌数据集中的应用具有显著的优势和效果,能够提高预测准确性、简化模型、减少计算复杂度和可视化数据。 import pandas as pd from sklearn.datasets import load_breast_cancer from sklearn.decomposition import PCA from sklearn.preprocessing import StandardScaler # 加载乳腺癌数据集 data = load_breast_cancer() X = pd.DataFrame(data.data, columns=data.feature_names) y = pd.Series(data.target) # 数据预处理 scaler = StandardScaler() X_scaled = scaler.fit_transform(X) # 使用PCA进行降维 pca = PCA(n_components=2) # 将数据降维到2维 X_pca = pca.fit_transform(X_scaled) # 输出降维后的数据 print(X_pca) |
|
转置矩阵 矩阵列与行的维度交换,就是以主对角线为主心轴,旋转180度后形成的矩阵,为原矩阵的转置矩阵 逆矩阵 矩阵A@矩阵B = 单位矩阵E ,则矩阵A与矩阵B互为逆矩阵 矩阵B = 矩阵A的伴随阵/矩阵A的行列式 正交阵 如果组成矩阵A的列向量a两两之间内积为1,则矩阵A为正交矩阵,简称正交阵 即组成矩阵A的列向量两两相互垂直, 任一列向量在其他向量方向上的投影为0,两两之间互不相交,没有线性重合的部分 但以上描述不是正交阵的定义,这也是正交阵特殊的地方 也就是说以上描述完全可以用于定义正交阵,但...那些写教材的数学家们却没有这么做 正交阵的定义如下: 矩阵A的转置矩阵@矩阵A = E ,则矩阵A为正交矩阵,简称正交阵 也就是说,这样的定义更能阐述正交阵的特性 应用 如果一个矩阵是正交阵,那么其逆就可以使用其转置替代,转置运算比逆运算要简单多了 相似矩阵,P的逆矩阵@A@P 如果P为正交阵,那么相似矩阵可以变换为P的转置 U,S,V = np.linalg.svd(A) U与V皆是正交矩阵 方阵中对称阵比较特殊,以对称阵举例说明SVD import numpy as np A = np.array([[3, 5, 7], [5, 1, 0],[7,0,3]]) U,S,V = np.linalg.svd(A) U.shape,S.shape,V.shape ((3, 3), (3,), (3, 3)) 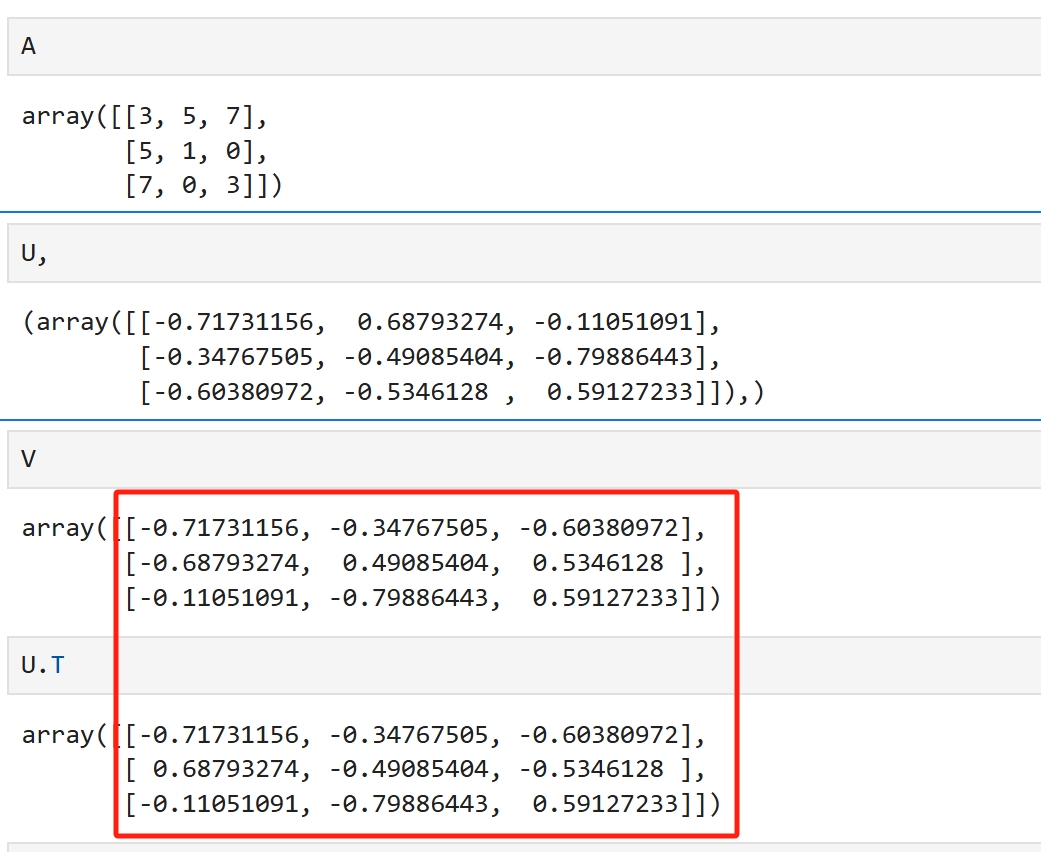
当A为对称阵时,U的转置就是V,由于U是正交矩阵,U的转置就是U的逆,于是此时的SVD就是 V的逆矩阵,S,V = np.linalg.avd(A) 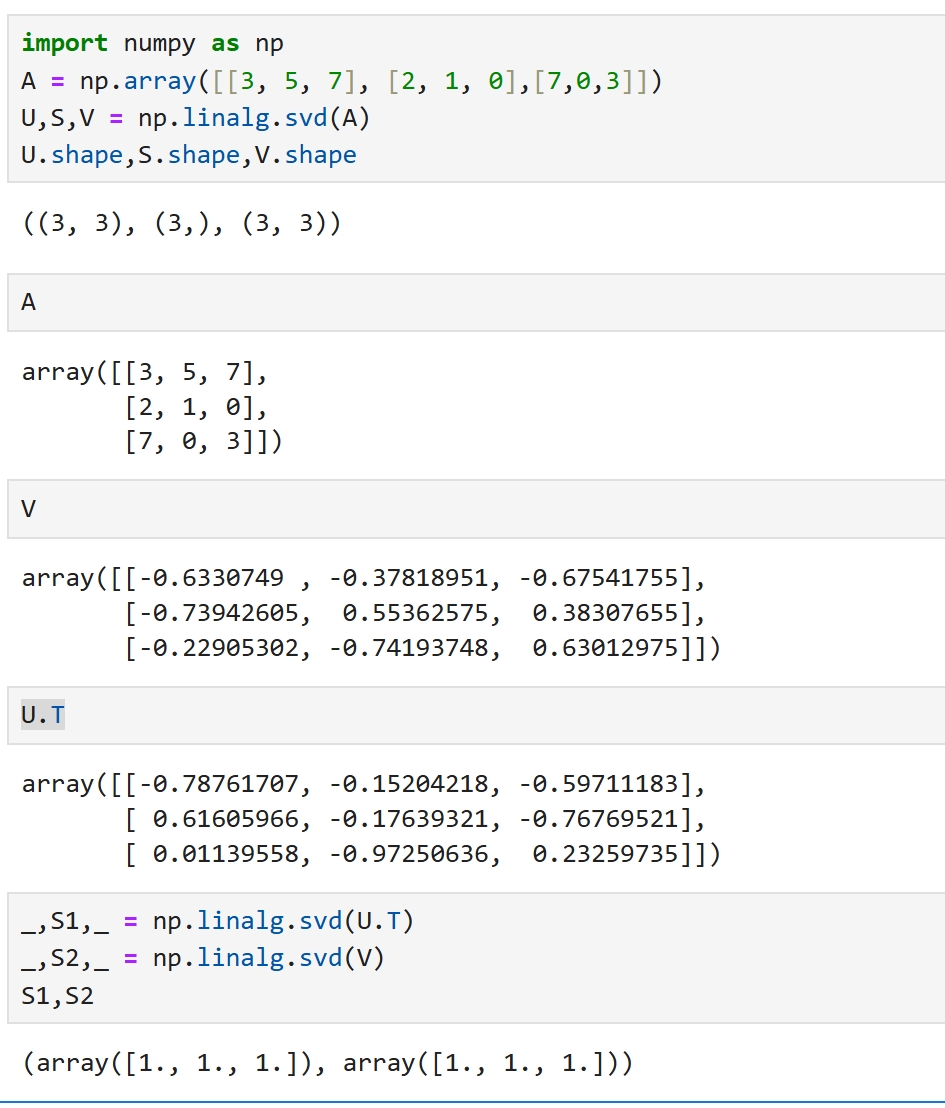
当A不为对称阵时,U与V不再满足这种关系,但它们依然是正交矩阵, 其特征值都是1,其结构依然是比较相似的 V[:,1]@V[:,2] -2.7755575615628914e-16 V[:,1]@V[:,0] 8.326672684688674e-17 V[:,2]@V[:,0] -5.551115123125783e-17 |
U,S,V = np.linalg.svd(A) 矩阵A@矩阵V的转置 即可实现降维 U中的列与S对应,V中的行与S对应,V转置后变为其列与S对应 一列就是一个维度的计算,取多少列,就会生成多少维,少生成点列,就是降维...
打开IDE,本人使用的是vscode,输入下面的代码,前提是已配置好python环境
from sklearn.decomposition import PCA
按下Ctrl键,鼠标点击PCA,就是去查看源码
class PCA(_BasePCA):
"""Principal component analysis (PCA).
Linear dimensionality reduction using Singular Value Decomposition of the
data to project it to a lower dimensional space. The input data is centered
but not scaled for each feature before applying the SVD.
...
...
...
"""
基于奇异值分解的线性降维
Linear dimensionality reduction using Singular Value Decomposition
一种线性降维方式,使用SVD
|
|
|
numpy与pandas互转
import numpy as np
import pandas as pd
def numpy2pd(mat):
"""
numpy 转 pandas,列的名称默认为0,1,2,...
"""
mat = pd.DataFrame(mat)
return mat
def pd2numpy(mat):
mat = np.array(mat)
return mat
numpy 数字类型
计算机中都是浮点运算,定位科学计算的numpy的两个主要类型: np.float32 np.float64 通常情况下,np.float32 够用并且相比np.float64节省计算资源 np.array(a).astype(np.float32)
import numpy as np
np.array([1.0]).dtype # dtype('float64')
np.NaN #nan np.inf,-np.inf #(inf, -inf) np.pi,np.e #(3.141592653589793, 2.718281828459045)
numpy shape转换
|
shape
### shape
- 查看矩阵或者数组的维数
- (),单个数字没有维度
- (m1,) 向量或1维矩阵
- (m1,m2) 2维矩阵
- (m1,m2,...,mn) n维矩阵
- 元素个数=m1*m2* ... *mn
```python
import numpy as np
from numpy.core.fromnumeric import shape
print(shape(3)) # (),没有
print(shape([3])) # (1,),表示第一维的个数为1,第二维没有
print(shape([[1],[2]])) # (2, 1) 第一维个数为2,第二维个数为1
print(shape([[1,1],[2,2]])) # (2, 2) 第一维个数为2,第二维个数为2
print(shape([[[1,1],[2,2]]])) # (1, 2, 2),第一维个数为1,第二维个数为2,第三维个数为2
print(shape(
[
[[1],[255]]
]
)) # (1, 2, 1), 第一维个数为1,第二维个数为2,第三维个数为1
print(shape(
[
[
[[1],[255]],
[[0],[100] ],
]
]
)) # (1, 2, 2, 1), 第一维个数为1,第二维个数为2,第三维个数为2, 第四个维度为1
```
|
|
reshape
### reshape
- 将原数组中的所有元素串起来,按新的维度进行组合
```python
import numpy as np
a = np.array( [
[
[[1],[255]],
[[0],[100] ],
]
])
print("1",a)
print("2",a.shape)
b = a.reshape(2,2)
print("3",b)
```
```
1 [[[[ 1]
[255]]
[[ 0]
[100]]]]
2 (1, 2, 2, 1)
3 [[ 1 255]
[ 0 100]]
```
-------------------------------------------------------------------------- |
|
reshape(-1, 1)
- 这里的-1被理解为unspecified value,意思是未指定,未给定的。
- 为-1时,该维度由程序自动决定
- 即将矩阵的shape转换为n行一列
```python
x = np.array(range(1, 10)).reshape(-1, 1)
print(x)
```
```
[[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]]
```
```python
x = np.array(range(2, 10)).reshape(2, -1)
print(x)
```
```
[[2 3 4 5]
[6 7 8 9]]
```
```python
# 原始数据的标签,是1维数据,每个样本向量对应一个标量
# 将标签变成列向量
y_train = y_train.reshape((-1,1))
y_test = y_test.reshape((-1,1))
```
|
|
X.reshape(-1) X.reshape(-1) 将n维矩阵转1维矩阵,即向量 效果等同于flatten 
|
|
|
numpy 新增加一个维度
np.newaxis
将np.newaxis放在哪一维表示在哪一维上增加一个维度 import numpy as np arr=np.random.randn(2,3) print(arr.shape) # (2, 3) a=arr[np.newaxis,:] print(a.shape) # (1, 2, 3) a=arr[:,np.newaxis] print(a.shape) # (2, 1, 3) a=arr[:,:,np.newaxis] print(a.shape) # (2, 3, 1)
reshape
原来的shape为(n1,n2,n3) 新加一个维度,reshape(n1,1,n2,n3) 这个1写在哪个位置就表示新增维度放在哪里
numpy条件过滤
### 取数组中满足某个条件的数据
```python
import numpy as np
a = np.arange(start=-5,stop=10)
print(f"a={a}")
print(a>0)
a = a[a>0]
print(a)
```
```
a=[-5 -4 -3 -2 -1 0 1 2 3 4]
[False False False False False False True True True True]
[1 2 3 4]
```
关键在于生成真假列表的逻辑,怎么生成的不重要,
只要能得到这个真假列表,就能得到对应的数组
如果有多个数组,完全可以混着写,写更复杂的表达式,
只要是条件表达式就可以
```
[False False False False False False True True True True]
```
参考文章
numpy数组拼接方法介绍(concatenate)