样本
统计 一类事物,比如统计某个城市的人均收入,所有人构成的集合是全体数据 但现实中不会真的统计该城市的所有人,或者说收集该城市每一个人收入这个思路不现实 实际会按某种方法抽取一部分人,用这部分人的收入近似代表该城市所有人的收入 这部分人就称为样本
方差
统计学中方差公式: (样本集合-样本均值)的平方和/(样本个数-1) 方差反映的数据分布的离散程度, 如果样本集合中每个元素皆相同,则完全集中,离散程度为0 反之,方差越大,离散程度越高,数据越分散,越不集中 序列数据 各个对应位置上的元素做差 此时,若相加,则有可能出现正负相加抵消的可能, 平方就避免了这个问题,平方后再相加,只要有对应位置上的元素不同,就能体现出差异 AI的计算如下: ((X - mean) ** 2).mean() (样本集合-样本均值)的平方/样本个数 这里也体现了AI的处理方式,参考数学理论,但不一定会完全照搬
MSE
人工智能中的MSE指模型预测与真实标签之间的均方误差,计算公式如下: ((y_pred - y_test) ** 2).mean() MSE与方差计算方式基本一致,区别如下: 方差计算的是同一个数据分布的离散程度 MSE计算的是两个数据分布之间的离散程度,模型数据分布与真实标签数据分布 MSE可以作为回归问题的损失函数
RMSE
RMSE(Root Mean Square Error,均方根误差)
是衡量模型预测值与真实值之间差异的一种常用指标。
它通过对预测误差进行平方、求平均、再开方的方式,
使得误差值具有与原始数据相同的量纲,从而便于理解和比较。
RMSE越小,表示模型的预测性能越好,即预测值越接近真实值。
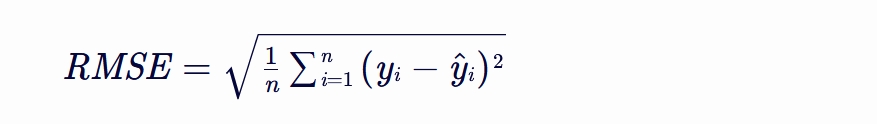
其中,n 是样本数量,yi 是第 i 个样本的真实值,y^i 是第 i 个样本的预测值。 RMSE 的优点在于它对较大的误差非常敏感,能够很好地反映出模型预测中的极端情况。 然而,它也有一些缺点,比如当数据中存在异常值时,RMSE 会受到较大的影响,导致评估结果不够稳健。 此外,RMSE 的量纲与原始数据相同。
|
|
|
|
|
|
|
|
统计学意义
统计学意义是什么意思
人根据经验而判断,观点经常带着自己的“美好愿望”,平时聊聊天还行,但很少用于重大决策 比如“问:什么时候下雪,答:冬天会下雪”,反面是 "不是冬天就不下雪", 但若来一股西伯利亚寒流,夏天也能下个冰雹, 更没有提及这地球上有些地方常年不下雪
足够广的覆盖面
以事实说话,且事实的量足够大,大到可以少代多,具有普遍意义的程度 原因在于个人的经验太片面了,是现实世界一个极小局部的反映, 其本身有着特殊性,局部性,随机性,不同人对同一事物的认知层次也有差异 解决方案就是多收集一些,求出所收集事物的共性,这样得出的结论 具有更强的参考意义 这就是统计学意义, 意思就是 有大量客观现实可依,具有较高的参考价值,可用于重大决策, 比如投票选举 但要注意,具有统计学意义 并不表示一件事必定如此,它只是表示很大概率如此, 在数据量足够大的情况才会出现必然性,才会“必定”如此, 也不表示永远如此,它也有其时效性,有其讨论范围
零假设与P值
普通人说假设,我认为 A与B的关系 是... 通常是一个肯定语 但关键问题在于, 是... 后面的内容不能统一,很难用数字量化, 不能数字量化的话,只靠语言描述那是文学... 在数字中,0 这个数字,通常表示没有,可能性为0,表示不可能, 从概率的角度看0,就是概率为0,代表着不可能,某件事不可能发生 我们从反面看这个 肯定语气的假设,就是 认为A与B没有关系,不可能 从统计学来看,就是 假定两件事之间存在关联的可能性是0,概率P值是 0 然后,通过一系列计算得到其概率p为0.05, 即 “认为A与B没有关系,不可能 ”这个假定成立的可能性为5%, 反过来就是 “A与B有关系”的可能性为 95%
最初那个否定式的假设,从概率角度看,就是说两件事相关的概率为0,所以也叫 零假设
|
|
P值
定义:
P值是在原假设为真的条件下,观察到的数据(或更极端的数据)出现的概率。
用途:
P值用于帮助我们判断观察到的数据是否与原假设相符。
如果P值很小,
说明观察到的数据在原假设为真的条件下出现的可能性很小,从而拒绝原假设。
统计学中的P值 在统计学中,由于假设是零假设,当零假设的概率 是1%不可能的时候,其显著性就很强 是0.1%的时候,那就是强的不得了 , 极强 意义有范围,事物有边界,假设也是如此, 从统计学的角度,定下一个边界,过了此界不再具有统计学意义, 这个边界值就是P值,通常P=0.05 即零假设概率p低于 P值0.05 时,具有统计学意义 P值提前就知道了,它是怎么来的? 它是根据以往的实验来的,是个经验值, |
|
|
|
|
|
|
显著性
统计学中的显著性
一件在人们看来必然发生的事,一眼看过去就能看的明明白白,没什么争议的事,显著性就很强 在统计学说一件事 发生或不发生的可能大小用 显著性 进行描述 显著性有两个方向: 一个是99%可能,也可描述为 1%不可能, 一个是99%不可能,也可描述为 1%可能 即一件事在概率的两端的时候,具有显著性统计学意义; 如果一件是不确定,发生与不发生的概率都是50%,这就没什么可显著的,也没有统计学意义
标准差
标准差 = 方差的 开平方
公式:
$\displaystyle \sqrt \frac{\displaystyle \sum_{i=1}^n \big(X - E(X)\big)^2}{n}$
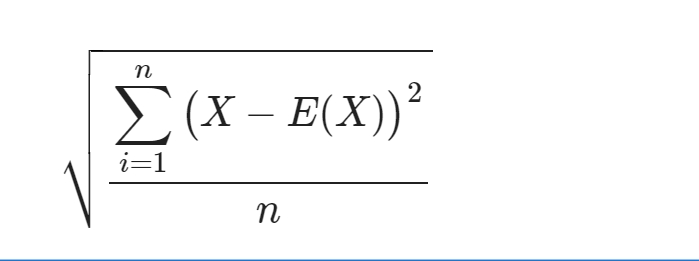
代表平均距离,平均离散程度
标准差特点
- 平均值,看的是整体,是团队,不关注个体
- 自身,是一个数据分布内元素分布的平均密度,离散程度
- 同一数据空间/同一量纲,
平方后再开方,就是求个距离,虽然涉及了平方求和,
但仍与原数据存在于同一数据空间
协方差
|
协方差的概念 对于两个数据分布X,Y , 如果近似满足下面的关系 Y = aX + b 则称分布X与分布Y之间的关系为线性关系 用EX表示X分布的均值,EY表示Y分布的均值 COV(X,Y) = SUM((xi - EX)(yi - EY)) / n 方差中误差的平方再求和,误差并不会相互抵消, 而协方差是两个分布的误差相乘再相加,那么中间必然会相互抵消 如果其结果为正,表示两个分布正相关,即一个增加,另外一个也增加 如果其结果为负,表示两个分布负相关,即一个增加,另外一个则减小 如果其结果为0,表示两个分布不相关,即X与Y相互独立 协方差的精确度 如果结果为0, 可以稍微信一下,但不能做为重要判断的依据 如果结果比较大,表示两个分布之间的线性相关性的可能较大 注意说的是可能,可能比概率还不准的, 概率90%成立,但真实结果是否成立还是两说的, 最好用散点图画出来看一下
|
协方差(Covariance)是统计学中 用于评估两个随机变量之间线性关系的强度和方向的一个度量。 它衡量了两个变量如何一起变化: 如果一个变量增加时,另一个变量也倾向于增加,则协方差为正; 如果一个变量增加时,另一个变量倾向于减少,则协方差为负; 如果两个变量之间没有线性关系,则协方差可能接近零 (尽管理论上并不总是如此,特别是在样本量较小或存在极端值时)。 为什么协方差依赖于线性关系?
协方差通过计算两个变量与其均值之差的乘积的平均值来工作。
这种计算方式本质上是在检测两个变量之间是否存在一种直接的、线性的相互影响。
如果两个变量之间的关系是非线性的(例如,指数关系、对数关系或更复杂的关系),
协方差可能无法准确地描述这种关系的强度和方向。
线性关系,指数学上的1维,1阶,1次型的映射关系,可以多元,比如,
y = ax + b,y=x1+x2 +b 都是线性关系
ax+b是x的一个线形组合,以y名称;
如果两个变量之间无法通过y=ax+b的形式表示,就表示它们 线性无关
如果两个数据分布不符合线性关系,可以判断吗?
虽然协方差主要用于描述线性关系,
但在某些情况下,即使两个变量之间的关系不是完全线性的,
协方差也可能提供一些关于它们之间关系的线索。
然而,对于非线性关系,协方差可能不够准确或全面。
为了更准确地描述两个变量之间的非线性关系,可以使用其他统计方法,如:
相关系数:
虽然皮尔逊相关系数(Pearson correlation coefficient)也基于协方差,
但它对线性关系更为敏感。
对于非线性关系,斯皮尔曼等级相关系数(Spearman's rank correlation coefficient)
或肯德尔等级相关系数(Kendall's tau coefficient)可能更适用。
回归分析:
回归分析不仅可以检测线性关系,还可以用来建模和预测变量之间的非线性关系。
通过选择合适的回归模型(如多项式回归、逻辑回归等),
可以探索和描述更复杂的非线性关系。
散点图:
通过观察两个变量的散点图,可以直观地判断它们之间是否存在线性或非线性关系。
散点图提供了关于数据分布和可能关系的直观视觉表示。
综上所述,虽然协方差主要关注线性关系,
但在处理非线性关系时,可以结合其他统计方法和可视化工具来获得更全面的理解。
回归分析 比如线性回归,就是y=ax+b的形式, 通过模型学习,如果预测不准,其中一个可能是模型不准 而模型是线性关系,模型不准,就代表两个变量之间不存在线性关系 |
ax+b是x的一个线形组合,以y名称; 如果两个变量之间无法通过y=ax+b的形式表示,就表示它们 线性无关 线性无关,就代表在1维这个层面上,它们有特性:只有自己有,其他事物没有 一个平面上的两个点,是必定可以通过y=ax+b的形成建立联系的 因为面由线组合,且两个点可以确定一个线 如果现在存在两个点,它们无法通过y=ax+b的形式表示,就是线性无关, 那么它们必定不会存在于一个“平 面”中,甚至不在一个数据空间中
比如,y=x1+x2+x3,如果y是一个3维空间的事物,
那么它是无法通过x1,x2,x3中的 两个/1个 线性表示的,多了可以,少了不行
3维空间中由x,y,z构成的坐标系中,其空间内任何一个点
与一个2维平面坐标系中的点 都是线性无关的,
因为它们根本就不在一个数据空间中,
简言之,就在2维的空间中,无法使用线性关系表示一个3维事物,
可以像/近似,但它不是
无法沟通,不能有一个共识,往往两者不在一个维度上
|
|
|
|
|
皮尔逊相关系数
卡方验证
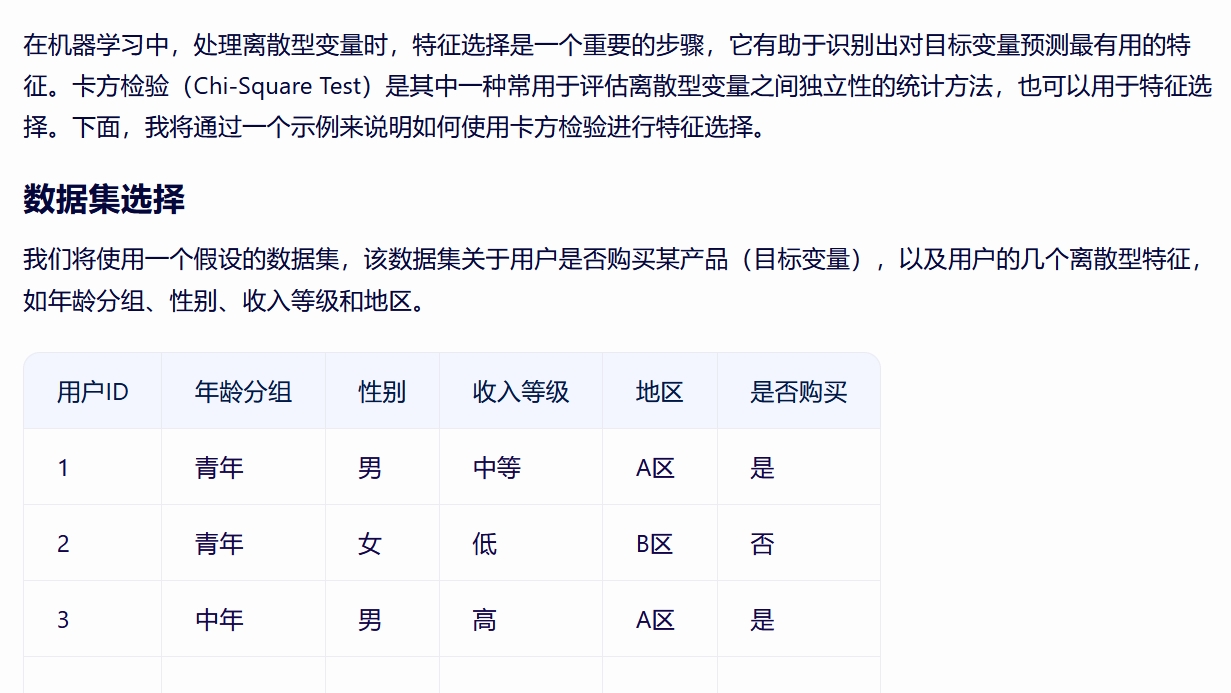



难点解释 零假设:两个变量相互独立,即相互之间的变化不受对方影响 预期频数是基于零假设预期的,即预期频数就是期望相互独立的频数 如果观察数与期望的相互独立的频数之间有较大的差异, 则认为两个变量之间相互独立的可能较小,即有显著相关性 误区1:认为卡方值越小两个变量越不相互独立 有这样的误区很可能是因为认为观察数与频数是两个变量的值 实际上,不是 这里的分类标签,是离散值,比如,性别是男,女,年龄划分,青年,中年,老年也是类别 观察数与频数都是统计一个类别的个数,而不是类似连续型变量的一个值 自由度 在卡方检验中, 自由度是指独立变量中可自由变化的数量,与总体样本量和观察结果有关。 对于三行四列的卡方检验,需要计算的自由度为(3-1)*(4-1)=6。 因此,三行四列卡方检验的自由度为3是错误的。正确的自由度应该是6。 在实际应用卡方检验时,正确计算自由度是非常重要的, 因为自由度的大小会影响到统计结果的可靠性和显著性。 如果自由度计算错误,可能会导致统计结论出现偏差或错误,从而影响研究结论的准确性。 为了避免自由度计算错误,需要在进行卡方检验前仔细检查数据的分类和计数, 确保每个分类都被正确计算,并按照正确的公式计算自由度。 除了卡方检验,自由度也是其他统计方法中常见的概念, 例如t检验、方差分析等。 在使用这些方法时,也需要正确计算自由度,以确保统计结果的准确性和可靠性。 |
在卡方检验的上下文中,观察频数(O)是实际观测到的数据频数, 而期望频数(E)是在假设特征与目标变量独立的情况下, 根据边缘分布(即每个变量的单独分布)计算出的预期频数。 观察频数(O) 观察频数(O)直接来自你的数据集。 在交叉表中,每个单元格的值都是观察频数, 表示在该特征值和目标变量值组合下的实际观测次数。 期望频数(E) 期望频数(E)是根据每个特征的 边缘分布(即不考虑其他特征时,该特征每个类别的出现次数)和 目标变量的边缘分布(即不考虑其他特征时,目标变量每个类别的出现次数)计算得出的。 具体地,对于交叉表中的每个单元格,期望频数可以通过以下公式计算: 
其中,Eij 是交叉表中第i行第j列的期望频数, 行i的总数是特征在第i个类别下的观测次数总和, 列j的总数是目标变量在第j个类别下的观测次数总和, 总观测数是数据集中的观测总数。 Python代码示例
import pandas as pd
# 示例数据
data = {
'年龄分组': ['青年', '青年', '中年', '老年', '中年', '青年'],
'是否购买': ['是', '否', '是', '否', '是', '是']
}
df = pd.DataFrame(data)
# 使用pandas的crosstab创建交叉表,这里的O就是交叉表中的值
cross_tab = pd.crosstab(df['年龄分组'], df['是否购买'])
print("观察频数(O):")
cross_tab
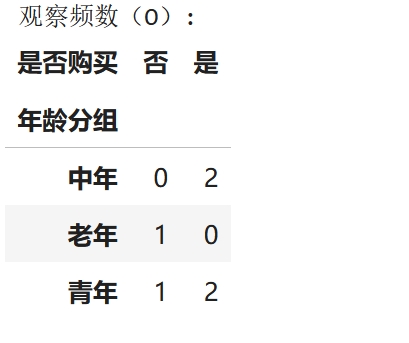
# 手动计算期望频数(E)
# 首先计算边缘分布
row_sums = cross_tab.sum(axis=1) # 年龄分组的边缘分布
col_sums = cross_tab.sum(axis=0) # 是否购买的边缘分布
total_obs = cross_tab.sum().sum() # 总观测数
row_sums,col_sums,total_obs
(年龄分组
中年 2
老年 1
青年 3
dtype: int64,
是否购买
否 2
是 4
dtype: int64,
6)
# 初始化期望频数矩阵,与交叉表同形 expected_freq = pd.DataFrame(0, index=cross_tab.index, columns=cross_tab.columns) 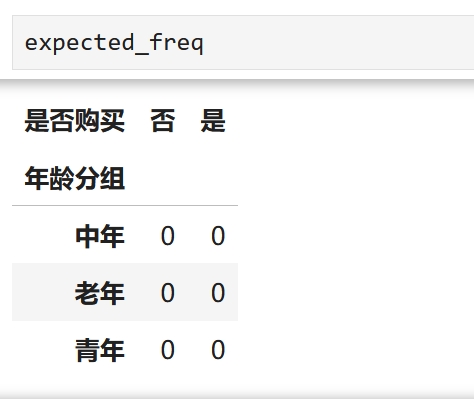
# 计算每个单元格的期望频数
for i in range(len(row_sums)):
for j in range(len(col_sums)):
expected_freq.iloc[i, j] = (row_sums[i] * col_sums[j]) / total_obs
print("\n期望频数(E):")
print(expected_freq)
# 注意:这里我们手动计算了期望频数,但通常你会直接使用chi2_contingency的结果
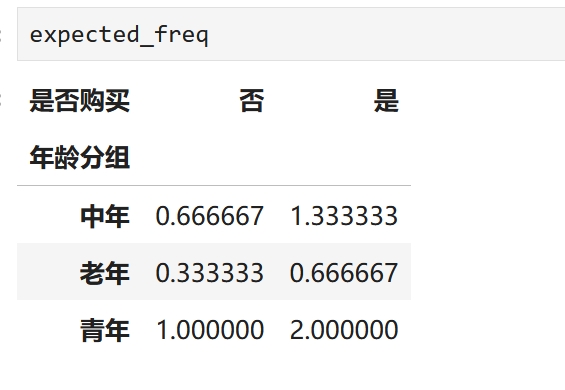
|
|
观察值O与期望频数E越接近,卡方值越小,就代表着所观察的列与目标列越相似,越接近,卡方值越大,就代表着观察列与目标列相关性越差,越没有关联,这样理解对吗? 您的理解基本上是正确的,但有一些细微的差别需要澄清。 在卡方检验中,观察值O与期望频数E之间的差异被用来评估两个变量之间的独立性。 卡方值(χ2)实际上是通过将这些差异的平方除以期望频数(即∑E(O−E)2)来计算的。 卡方值越小 这通常意味着观察频数与期望频数之间的差异越小, 即实际观测到的数据分布与在假设两个变量独立时预期的数据分布越接近。 因此,较小的卡方值支持两个变量之间可能独立的假设, 但这并不直接等同于说两个变量“越相似”或“越接近”。 相似性或接近性在这里的语境中可能有些误导,因为卡方检验关注的是独立性而非相似性。 卡方值越大 这表示观察频数与期望频数之间的差异越大, 即实际观测到的数据分布与在假设两个变量独立时预期的数据分布相差较大。 较大的卡方值提供了拒绝两个变量独立假设的证据,即两个变量之间存在某种关联或依赖关系。 然而,这并不直接等同于说两个变量“相关性越差”或“越没有关联”, 而是说它们之间的关联或依赖关系比预期的要强。 重要的是要注意,卡方检验的显著性(即P值) 才是决定我们是否拒绝零假设(两个变量独立)的关键因素。 即使卡方值很大,但如果P值大于显著性水平(如0.05),我们也不能拒绝零假设。 同样,即使卡方值很小,如果P值小于显著性水平,我们也会拒绝零假设, 认为两个变量之间存在显著的关联或依赖关系。 因此,更准确的表述可能是: 在卡方检验中,较小的卡方值通常意味着两个变量之间的独立性假设更有可能成立, 而较大的卡方值(伴随较小的P值)则提供了拒绝这一假设的证据, 表明两个变量之间存在显著的关联或依赖关系。 |
import pandas as pd
from scipy.stats import chi2_contingency
# 示例数据
data = {
'用户ID': [1, 2, 3, 4, 5],
'年龄分组': ['青年', '青年', '中年', '老年', '中年'],
'性别': ['男', '女', '男', '女', '女'],
'收入等级': ['中等', '低', '高', '低', '中等'],
'地区': ['A区', 'B区', 'A区', 'C区', 'B区'],
'是否购买': ['是', '否', '是', '否', '是']
}
df = pd.DataFrame(data)
# 假设我们想要检验“年龄分组”和“是否购买”之间的独立性
# 使用crosstab创建交叉表
cross_tab = pd.crosstab(df['年龄分组'], df['是否购买'])
# 执行卡方检验
chi2, p, dof, expected = chi2_contingency(cross_tab)
# 打印结果
print("卡方统计量:", chi2)
print("P值:", p)
print("自由度:", dof)
#-------------------------------------------------------------------------
# 类似地,你可以对其他特征进行相同的检验
# 例如,检验“性别”和“是否购买”之间的独立性
cross_tab_gender = pd.crosstab(df['性别'], df['是否购买'])
chi2_gender, p_gender, dof_gender, expected_gender = chi2_contingency(cross_tab_gender)
# 打印性别相关的检验结果
print("\n性别与是否购买的卡方检验:")
print("卡方统计量:", chi2_gender)
print("P值:", p_gender)
卡方统计量: 2.9166666666666665 P值: 0.2326236579172927 自由度: 2 性别与是否购买的卡方检验: 卡方统计量: 0.31250000000000006 P值: 0.5761501220305787
chi2_gender:
这是一个统计量,即卡方值(Chi-square value)。
在性别(或其他分类变量)的卡方检验中,它表示观察频数与期望频数之间的差异大小。
卡方值越大,说明观察频数与期望频数之间的差异越大,
即变量之间可能存在显著的关系。
p_gender:
这是一个概率值(P-value),用于判断观察到的数据差异是否显著。
在统计学中,P值用于量化观察结果是由随机性造成的还是由于真实差异造成的。
通常,如果P值小于一个预先设定的显著性水平(如0.05),
则认为观察到的差异是显著的,即拒绝原假设(如“性别与某变量无关”的假设)。
dof_gender:
这代表自由度(Degrees of Freedom, DoF)。
在卡方检验中,自由度是指数据中能够自由变动的观测值的数量,
用于计算卡方分布的临界值。
在分类数据的卡方检验中,自由度通常等于(类别数-1)乘以(行数-1),
其中“类别数”和“行数”取决于你的数据表(列联表)的结构。
expected_gender:
这个名称可能不直接对应于卡方检验的常规输出,
但根据上下文,
我们可以推测它指的是在假设性别与另一变量(如疾病、偏好等)独立的情况下,
性别分布的期望频数。
在卡方检验中,通常会计算每个单元格的期望频数,以与实际观测到的频数进行比较。
这些期望频数是基于行和列的总数,在假设行和列独立的情况下计算得出的。
这里判断的依据,依卡方进行判断,可以认为卡方大于4时,两个变量有显著相关性 |
|
|
多重共线性
多重共线性是什么
在线性代数中,指y=ax+b,就是一组向量可以用另外一组向量表示, 在解析几何中,指两条平行的直线,变化的趋势一致, 在统计学中,指两个数据的分布变化一致/差不多(因为统计学并不像数学那么严格),
线性模型的变量筛选
在变量进入线性模型之前,如果存在多组共线性的变量,举例如下: x0 + w1*x1 + w2*x2 + w3*x3 + w4*x4 + w5*x5 + ... + wn*xn = y 现在的问题是,(x1,x2,x3)可以用(x4,x5)近似表示, 但在训练的过程中,每个系数前都是有参数的,增加变化的量, 会加长训练的时间,并且模型结果的方差会变大... 现象是模型变得不怎么稳定 当然了,作为万能公式,是否去除 具有多重共性线的变量,最终影响并不是很大
WOE
Evidence 英/ˈevɪdəns/ 美/ˈevɪdəns/
n. 证据;(法庭上的)证据,证词,人证,物证;证明;根据
在机器学习中,WOE(Weight of Evidence)即证据权重,
是一种用于衡量一个变量对于某个事件的预测能力的指标,
特别是在信用评分、风险评估、欺诈检测等场景中广泛使用。
特征,分箱, 比例差异
WOE通过对变量进行分组(也称为离散化、分箱)并计算每个分组中好坏样本的比例差异,
来评估该变量对目标事件(如违约、欺诈等)的预测能力。

注意事项
分箱处理:
WOE的计算依赖于对变量的分组处理。
分组的好坏会直接影响WOE的计算结果和模型的性能。
因此,在实际应用中需要仔细考虑分组策略。
小概率事件:
当某个分组中的样本数量很少时,可能会导致WOE的计算结果不稳定或失去意义。
此时需要采取相应的处理措施,如合并分组或调整模型参数等。
分组相对整体的比例 当我们谈论“好样本的比例”时, 我们实际上是在说该分组中好样本数量占该分组总样本数量的比例(Goodi/(Goodi+Badi)), 但这个比例并没有直接出现在WOE公式中。 WOE公式中的比例是相对于整体样本而言的, 即每个分组中的好样本比例与整体好样本比例的比较, 以及每个分组中的坏样本比例与整体坏样本比例的比较。 
澄清误解
关于“WOE>0,则表示好样本的可能性大于整体平均水平”的表述,
需要澄清的是:
WOE值大于0并不直接表示“好样本的可能性大于整体平均水平”,
而是表示在该分组中,好样本相对于坏样本的“富集”程度高于整体平均水平。
这里的“富集”程度是通过 比较分组内和整体中 好坏样本的比例来衡量的。
因此,在解释WOE值时, 我们应该关注它如何反映了分组中好坏样本比例的相对变化, 而不是直接将其与“好样本的可能性”或“坏样本的可能性”的绝对水平相联系。 ln函数的增函数性质确保了当分组中好样本相对于坏样本的富集程度高于整体时,WOE值会大于0。
|
将数据分段,即不管数据分布什么结构,直接将其投影到一个数轴(1维结构)上,
开始分段对比
从某个维度/按照某个方法 观察两个分布的中好坏样本的 比例差异
差异大,表明该特征很容易区分数据,
即从这个维度 区分一个数据的好与坏 相对容易一些
这里面涉及的思想有:
线性处理:
复杂问题简单化,以线性的眼光看待一切复杂问题,降维处理
离散化:
以点代线,降低数量级,除了降低运算量之外,
更重要的是合并后的数据算法处理起来更容易
微分:
当一个问题无处下手时,尝试将之拆分,比如,分类,分段,分步... 化大为小
|
|
|
|
|
|
|
IV值
在机器学习中,IV值(Information Value)常用于特征选择, 特别是在信用评分、风险评估等场景中。 IV值衡量了某个变量对目标变量预测能力的贡献程度,是特征筛选的一个重要量化指标。 IV值的原理 IV值的计算基于WOE(Weight of Evidence)值, WOE是对原始变量进行分组后,每个分组中好坏样本比例的一种编码形式。 IV值则进一步考虑了不同分组中样本数量的占比情况, 通过加权求和的方式计算得出。具体来说,IV值的计算公式如下: 
Pi(Good)指第i个分组的Good样本数量/全体Good样本数量 IV值的大小反映了变量对目标变量预测能力的强弱。 IV值越高,表示该变量的预测能力越强,对模型的贡献也越大。 连续/离散 在特征选择的方法中,IV值(Information Value)是一种非常有用的量化指标, 用于评估特征对目标变量的预测能力。 IV值既可以用于连续型变量,也可以用于离散型变量。 对于连续型变量 对于连续型变量,IV值的计算通常需要先进行分箱(binning)处理。 分箱的目的是将连续变量的取值范围划分为若干个离散的区间(即“箱子”), 以便在每个区间内计算IV值。 分箱的方法有多种,如等距分箱、等频分箱等。 分箱后,每个箱子内的样本被视为一个离散的类别, 然后就可以计算该箱子对应的IV值了。 对于离散型变量 对于离散型变量(如类别型变量),IV值的计算则相对直接。 离散型变量的每个类别都可以看作是一个“箱子”, 直接在该类别内计算响应比例和未响应比例, 进而计算WOE(Weight of Evidence)值和IV值。 IV值的计算原理 无论是连续型变量还是离散型变量,IV值的计算都基于WOE值。 WOE值表示了某一类别或箱子中“好样本”(或响应样本)与 “坏样本”(或非响应样本)的比例相对于整体样本中好坏样本比例的对数差异。 IV值则是所有箱子(或类别)的WOE值的加权和,用于衡量整个变量对目标变量的预测能力。 IV值的解释/范围
IV值的取值范围通常为[0, +∞)。
根据不同的IV值范围,我们可以将特征划分为不同的重要性等级,如
无用特征(IV<0.02)、弱价值特征(0.02<IV<0.1)、
中价值特征(0.1<IV<0.3)和强价值特征(0.3<IV<0.5)。
一般来说,IV值越高,表示该特征的预测能力越强,对模型的贡献也越大。
综上所述,IV值是一种非常灵活且有效的特征选择方法,
既可以用于连续型变量(通过分箱处理),也可以用于离散型变量。
在机器学习建模过程中,
我们可以根据IV值的大小来 筛选和排序 特征,
从而提高模型的性能和稳定性。
|
|
特征选择
得到所有特征的IV值后,我们可以根据IV值的大小进行特征选择。
一般来说,IV值较高的特征具有更强的预测能力,应该优先选择进入模型。
同时,也可以根据业务需求和模型复杂度来设定一个IV值的阈值,
只选择IV值大于该阈值的特征进入模型。
例如,在信用评分模型中,我们可能会选择IV值大于0.3的特征作为入模变量,
因为这些特征对违约风险的预测能力较强。
通过这种方式,我们可以有效地减少模型的复杂度并提高预测性能。
好样本与坏样本
在机器学习的上下文中,尤其是在分类问题(如信用评分、欺诈检测等)中,
好样本和坏样本通常指的是两种不同类别的实例。
这些类别是根据业务目标来定义的:
好样本:通常指的是符合业务期望或正面结果的实例。
例如,在信用评分中,好样本可能代表那些能够按时还款的客户;
在欺诈检测中,好样本可能代表那些没有欺诈行为的交易。
坏样本:则是指不符合业务期望或产生负面结果的实例。
在信用评分中,坏样本可能代表那些违约或逾期的客户;
在欺诈检测中,坏样本则代表那些被确认为欺诈的交易。
IV值的公式与解释
IV值(Information Value)是衡量变量预测能力的一个指标,特别是在分类问题中。
它基于WOE(Weight of Evidence)值计算得出,
用于评估变量中不同分组对目标变量(好/坏)预测能力的贡献。
IV值的计算公式通常涉及对每个分组计算WOE值,并基于这些WOE值进行加权求和。
IV值的高低并不直接反映好坏样本的绝对数量或比例,
而是反映了变量中不同分组之间好坏样本分布的差异程度。
当某个变量能够显著地区分好坏样本时(即某些分组中好样本比例远高于或远低于整体比例),
该变量的IV值就会较高。
机器学习中样本比例的要求
在机器学习中,确实存在一种普遍的观点,
即特征比较时最好保持样本的平衡(即好坏样本比例接近1:1)。
这是因为不平衡的数据集可能会导致模型偏向于多数类(即样本数量较多的类别),
从而降低对少数类(即样本数量较少的类别)的预测能力。
然而,这并不意味着IV值高的变量就一定要求坏样本不平衡。
IV值高仅仅说明该变量在区分好坏样本方面具有较高的预测能力,
而与其在数据集中的具体比例无关。
实际上,在某些业务场景中,坏样本(如欺诈行为、违约事件)本身就是稀有的, 因此数据集本身就会是不平衡的。 在这种情况下,我们仍然可以通过计算IV值来 评估 哪些变量 对于区分这些 稀有但重要的负面事件 是有价值的。 综上所述,好样本与坏样本是根据业务目标定义的两种不同类别的实例。 IV值的高低反映了变量在区分好坏样本方面的预测能力, 而与其在数据集中的具体比例(即是否平衡)无直接关联。 在机器学习中,虽然保持样本平衡是一个重要的考虑因素, 但IV值作为评估变量预测能力的指标,并不受此限制。
|
import pandas as pd
import numpy as np
# 构造数据集
np.random.seed(0)
data = {
'年龄': np.random.randint(20, 70, size=100),
'收入': np.random.randint(20000, 100000, size=100),
'简化信用评分': np.random.randint(300, 850, size=100),
'是否违约': np.random.choice([0, 1], size=100, p=[0.8, 0.2])
}
df = pd.DataFrame(data)
# 定义一个函数来计算IV值
def calc_iv(feature, target, bins=None, special_values=None):
if bins is None:
# 使用等频分箱,但注意qcut需要数值型数据
bins = pd.qcut(feature, q=4, duplicates='drop')
# 处理特殊值(如果有的话)
if special_values is not None:
for val in special_values:
feature = feature.replace({val: np.nan})
feature = feature.fillna(-1)
bins = pd.cut(feature, bins=bins.cat.add_categories([-1]), right=False)
# 创建包含分组和是否违约的DataFrame
grouped = pd.DataFrame({
'feature': feature,
'target': target
}).groupby(bins)
# 计算每个组的总数、违约数和未违约数
result = grouped.agg(
Total=('target', 'size'),
Bads=('target', lambda x: (x == 1).sum()),
Goods=('target', lambda x: (x == 0).sum())
)
# 计算分布和WOE
result['Distribution Goods'] = result['Goods'] / result['Goods'].sum()
result['Distribution Bads'] = result['Bads'] / result['Bads'].sum()
result['WOE'] = np.log(result['Distribution Goods'] / result['Distribution Bads'])
result['IV'] = (result['Distribution Goods'] - result['Distribution Bads']) * result['WOE']
# 返回总的IV值
return result['IV'].sum()
# 计算各特征的IV值
iv_age = calc_iv(df['年龄'], df['是否违约'])
iv_income = calc_iv(df['收入'], df['是否违约'])
iv_credit_score = calc_iv(df['简化信用评分'], df['是否违约'])
# 打印IV值
print("年龄的IV值:", iv_age)
print("收入的IV值:", iv_income)
print("简化信用评分的IV值:", iv_credit_score)
# 选择IV值大于0.3的特征(这里可能不会有特征满足条件,因为数据是随机生成的)
selected_features = [
feature for feature, iv in zip(['年龄', '收入', '简化信用评分'], [iv_age, iv_income, iv_credit_score])
if iv > 0.3
]
print("选择的特征:", selected_features)
由于数据集是随机生成的,因此计算出的IV值很可能是很低的,不足以用于实际的特征选择。
在实际应用中,特征的分箱(binning)策略非常重要,可能会影响IV值的计算结果。
上面的示例中使用了等频分箱(pd.qcut),
但这可能不是最佳选择,特别是在特征分布不均匀的情况下。
特殊值的处理(如NaN值)也是影响IV计算的一个重要因素。
在上面的示例中,我们将NaN值视为一个特殊的分组。
为了得到有意义的IV值,通常需要有一个足够大且具有代表性的数据集。
calc_iv函数接受特征列和目标变量列作为输入,并返回该特征的IV值。 在函数中,我们首先对数据进行分箱处理(如果需要处理特殊值,则在此之后进行), 然后计算每个分组的总数、违约数和未违约数,接着计算分布、WOE和IV,并最终返回总的IV值。 注意,在计算分布时,我们使用了sum()函数来确保分母是正确的(即所有好样本或坏样本的总和)。 离散型变量的每个类别都可以看作是一个“箱子”
import pandas as pd
import numpy as np
import random
# 构造数据集
np.random.seed(0) # 为了结果的可重复性
data = {
'年龄': np.random.randint(20, 70, size=15),
'收入': np.random.randint(20000, 100000, size=15),
'简化信用评分': np.random.randint(300, 850, size=15),
'是否违约': np.random.choice([0, 1], size=15, p=[0.8, 0.2]) # 假设大部分不违约
}
df = pd.DataFrame(data)
# 定义可能的职业类型
job_types = ['软件工程师', '数据分析师', '市场营销专员', '医生', '教师', '会计师', '银行职员', '自由职业者']
# 随机选择职业类型并添加到DataFrame中
df['职业类型'] = [random.choice(job_types) for _ in range(len(df))]
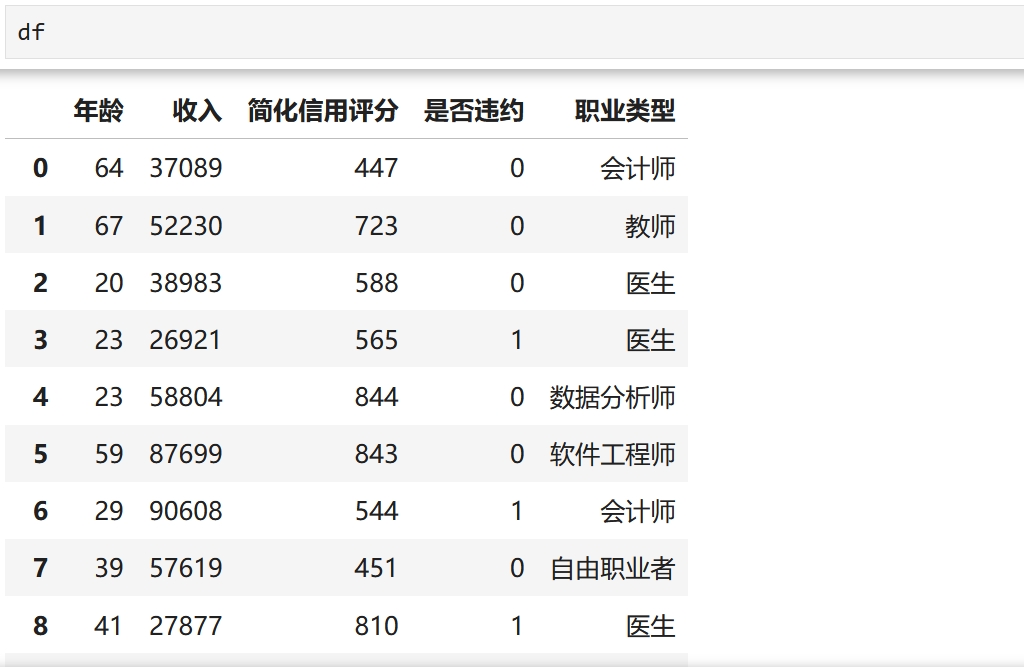
bins=df['职业类型']
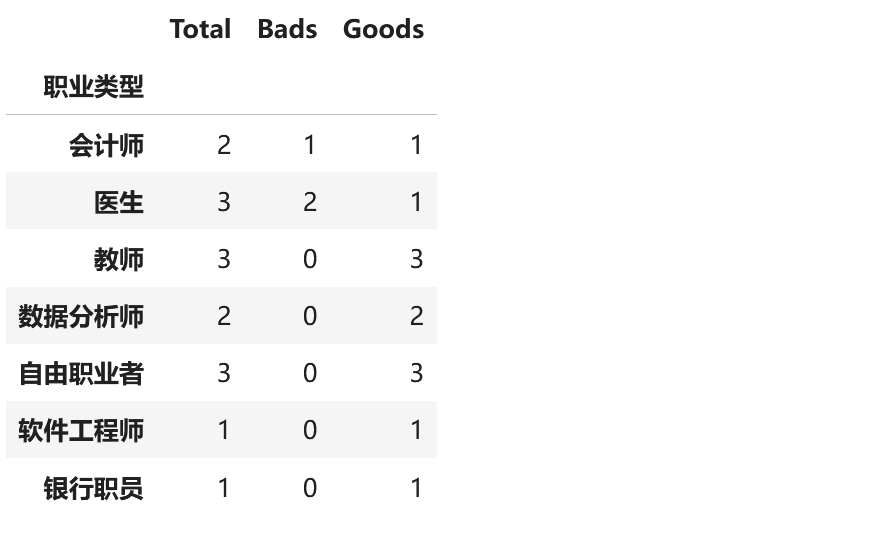
# 创建包含分组和是否违约的DataFrame
result = pd.DataFrame({
'feature': df['职业类型'],
'target': df['是否违约']
}).groupby(bins,observed=True).agg(
Total=('target', 'size'),
Bads=('target', lambda x: (x == 1).sum()),
Goods=('target', lambda x: (x == 0).sum())
)
result
|
|
|
|
|
VIF
线性表示其中的一个理解维度
本次从这个角度看线性表示: a + b + c = d 只要该公式成立,那么就自然有 a + b - d = -c a + c - d = -b 想表达的是,如果交换一个线性方程组的两个列,除了它们的系数变一下符号外,其余都不变 用一句表述, 如果一个列向量可以线性表示一组向量, 那么该向量组的任一向量都可以 表示 剩下的所有向量形成的 新的向量组 所以,可以求单个列对剩下所有列的线性相关线,可以使用逻辑回归来预测
方差膨胀因子VIF
Variance inflation factor, VIF, for one exogenous variable inflation: [ɪnˈfleɪʃn] 通胀率;通货膨胀 exogenous: [ekˈsɑːdʒənəs] 外源性的 VIFi = 1/(1 - Ri的平方) Ri: 将其中一列做为标签,剩下所有列作为数据,使用逻辑回归进行预测得到的结果 逻辑回归,0与1分类,0代表没关系,1代表有关系,得到一个概率值 VIF 可以检测自变量的多重共线性的共线程度 VIF越高,多重共线性的影响越严重; 由于没有VIF临界值表,我们只能使用经验法则: 若VIF>5,则存在严重多重共线性; 也有人建议用VIF>10作为存在严重多重共线性的标准,特别在解释变量多的情形应当如此。 在实际测试过程中,并非要指定一个VIF阈值, 比如某因子的VIF值超过阈值才剔除,而是通过观察所有因子值的VIF值, 如果发现该值较大(显著离群),剔除该因子即可。
sklearn vif计算示例
import pandas as pd
import numpy as np
from statsmodels.stats.outliers_influence import variance_inflation_factor
data = pd.DataFrame([[15.9,16.4,19,19.1,18.8,20.4,22.7,26.5,28.1,27.6,26.3]
,[149.3,161.2,171.5,175.5,180.8,190.7,202.1,212.1,226.1,231.9,239]
,[4.2,4.1,3.1,3.1,1.1,2.2,2.1,5.6,5,5.1,0.7]
,[108.1,114.8,123.2,126.9,132.1,137.7,146,154.1,162.3,164.3,167.6]]).T
# 上述数表,第0列为因变量(y/label),1、2、3列为自变量(x)
X = data[[1,2,3]]
# 注意,一定要加上常数项,如果没有常数项列,计算结果天差地别,可能VIF等于好几千
X[4]=1
print("第1列与剩下所有列的VIF=",variance_inflation_factor(X, 0))
print("第2列与剩下所有列的VIF=",variance_inflation_factor(X, 1))
print("第3列与剩下所有列的VIF=",variance_inflation_factor(X, 2))
print("第4列与剩下所有列的VIF=",variance_inflation_factor(X, 3))
输出:
第1列与剩下所有列的VIF= 179.722747043629
第2列与剩下所有列的VIF= 1.0234788725900321
第3列与剩下所有列的VIF= 179.84399383804046
第4列与剩下所有列的VIF= 66.60449485389634
参考
多元共线性检测 -- 方差膨胀因子(Python 实现)
多重共线性:python计算VIF以及使用vif做因子独立性检验的方法
利用Python进行VIF检验
