从数据到标签
|
从数据到标签概述
从数据到标签,可以一次到位,也可以嵌套,并且可以无限嵌套
嵌套与否在数学上 与不嵌套完全一致,在实际应用中,可以舍弃一部分,让一部分特征在变换中消失
固定的是数据与标签,变化是参数
- 从数据到标签的路径有N条
- 目的并不在于哪一条,而是可用的任一条
- 是大数定律与个体随机的综合体现,
- 只要找到其中一条满足业务条件的路径即可
- 局部的随机性是允许的,并且还可以体现其健壮性
全局视角 标签是目标,数据是起点,这中间有N条路可达,但 你 是不知道的 训练参数就是以暴力破解的方式,找到一条 ... 嗯 ... 最好是最短的那条路 每条路上有M个节点,每次线性变换 或 添加激活函数或某个组件 都可看作添加一个节点 , 但你不知道很客观真理那一方有哪些节点, 看看自己知道哪些 根据行业经验和自己的知识储备,开始试吧 ... 这张由节点与路径构成的图,就是全局视觉,但在我们眼里,那是啥也看不见... 只能慢慢搜索... 我们就是盲人摸象中的盲人,我们去摸索了,比信口开河强多了... 去模拟,去近似, 去探索...
|
|
数据决定上限 模型从历史数据中学习规律,数据有大量的噪声,干扰信息, 此时模型可能无论怎么训练都精度不高 ,或者说达不到要求
------------------------------------------------------------------------
|
|
绝对优势
从数据变换到标签,
对于每个样本,都配有一组参数,参数变换的目标在于
- 让得到的结果投放到一个标签中,即最接近其中的某个标签,可以将之想象成一个篮子,一个结果只能放一个框中
- 并且是仅有的一个标签中
- 要求是 多选一
- 得到的是一个概率,选概率最大的那个
- 每个结果都有一个概率
- 每个结果都是一个长度/维数为标签个数n的向量
- 这个n维向量做softmax,值最大的元素位置对应的索引所对应的标签
- 元素 -- 概率 -- 最大概率 -- 元素索引 -- 业务标签
- 最好的情况是,其中一个90%,剩下之和是10%
- 这就是绝对优势
但实际情况往往不是这样,可能是这样的
- 其中一个是20%,
- 剩下有一个0,其余是10%
- 这也算绝对优势
- 即被选择的标签相对其他标签有明显的差异
若是下面的情况
- 其中两个是51%,48%,其余所有之和为1%
- 这就导致没有任何一个结果具有 绝对优势
- 算法取最大值51%,
- 但要知道差异的2%相对51%,48%来说,并没有什么压倒性优势
- 并且算法每次都有波动,可能下次就是49%,49%
- 能出现这个结果的,通常是数据的原因
- 即数据属于这两个类型的哪个都可以
- 数据本身对于这两个类型来说,是模糊的,不清晰的,不容易区分的
- 比如人脸识别遇到了某些双胞胎,太像了,或者说,这世界上本身就存在某个与你高度相似的事物
- 这时通常有以下几种做法
- 进一步细分,添加一些变量,这些新增变量要对区分这两个类型有帮助
- 增加模型复杂度,添加更多的参数,再次训练
- 网上找找其他清洗数据的方法,或者请教一下他人,就是向外求助
- 接受这个现实,但给个提示,说也可能是另外一个类型,
- 就是在这里标注一下,告诉你这个结果,让人心里有个准备,多个选择
- 也是放一放的意思,或者后续就有解决办法了,至少现在点出了可优化的一点就在这里
|
|
|
|
|
线性变换分类
线性变换 产生的是值是一个连续的值
对于2分类问题,比如0,1二分类
大于0.5转换为1
小于0.5转换为0
这样就将连续问题,转换为 二分类问题
多分类问题
将模型的维度变换到1维上,经过上面的转换就是2分类
将模型的维度变换到n维上,经过softmax变换转换为n维上的概率后,就是多分类问题
自然概率
对于2分类问题,自然概率,即随机起步的概率,也不会太低...
经过训练的模型输出,要高于自然概率
|
MSE是针对的是连续型数据,线性Model到损失的计算依然是连续型问题
只是在数据输出之后,后处理上,转为分类
因此整个前身传播及反导求导,都是连续型数据的计算
所以损失函数“可以”使用MSE
import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
import torch
from torch import nn
from torch.nn import functional as F
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
# 加载数据集 X, y = load_breast_cancer(return_X_y=True) # 切分数据集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1) # 标签改为列向量 y_train = y_train.reshape((-1, 1)) y_test = y_test.reshape((-1, 1)) # 数据预处理 mean_ = X_train.mean(axis=0) std_ = X_train.std(axis=0) X_train = (X_train - mean_) / std_ X_test = (X_test - mean_) / std_
class MyDataset(Dataset):
def __init__(self, X, y):
self.X = X
self.y = y
def __getitem__(self, idx):
x = self.X[idx]
y = self.y[idx]
return torch.tensor(data=x).float(), torch.tensor(data=y).float()
def __len__(self):
return len(self.X)
# 批量化打包数据
train_dataset = MyDataset(X=X_train, y=y_train)
train_dataloader = DataLoader(dataset=train_dataset,batch_size=32 ,shuffle=True)
test_dataset = MyDataset(X=X_test, y=y_test)
test_dataloader = DataLoader(dataset=test_dataset,batch_size=32 ,shuffle=False)
# 定义模型
class Model(nn.Module):
def __init__(self, in_features=30, out_features=1):
super(Model, self).__init__()
self.linear1 = nn.Linear(in_features=in_features, out_features=out_features)
def forward(self, x):
out = self.linear1(x)
return out
# 生成模型对象
model = Model(in_features=30, out_features=1)
# 损失函数
loss_fn = nn.MSELoss()
# 优化器
optimizer = torch.optim.SGD(params=model.parameters(), lr=1e-2)
# 过程监控
def get_loss(dataloader, model=model, loss_fn=loss_fn):
losses = []
with torch.no_grad():
for X, y in dataloader:
y_pred = model(X)
loss = loss_fn(y_pred, y)
losses.append(loss.item())
return np.array(losses).mean()
# 计算准确率
def get_acc(dataloader=test_dataloader, model=model):
accs = []
with torch.no_grad():
for X, y in dataloader:
# 原始输出
y_pred = model(X)
# 类别转换
y_pred = (y_pred >= 0.5).float()
# 准确率的计算
acc = (y == y_pred).float().mean()
accs.append(acc.item())
return round(np.array(accs).mean(), ndigits=3)
# 训练函数
def train(dataloader=train_dataloader, model=model, loss_fn=loss_fn, optimizer=optimizer, epochs=100):
for epoch in range(1, epochs+1):
for X, y in dataloader:
# 正向传播
y_pred = model(X)
# 计算损失
loss = loss_fn(y_pred, y)
# 梯度清空
optimizer.zero_grad()
# 反向传播
loss.backward()
# 更新参数
optimizer.step()
print(f"Epoch: {epoch}, Train Acc: {get_acc(dataloader=train_dataloader)}, Test Acc: {get_acc(dataloader=test_dataloader)}")
train()
|
|
|
|
|
|
|
分类问题
回归问题 模型输出是数值
分类问题 模型输出是类别
类别与类别之间应该地位相当,
如果使用 index 编码,即0,1,2,...,n-1区分n个类别,那么类别与类别之间的差异过大
这里使用one hot编码 去标识一个类别
- 每个One Hot向量的长度皆为1,对应类别与类别之间地位相同
- 每个类别对应One Hot向量的1个维度,相同之间又有区别
- 类别所在维度为1,其他维度为0,这又与概率对应上了
实际上就是用一个向量去代表了标签,这个向量有以下特点 - 长度皆为1 - 所在类别为1,其他维度为0 - 向量的维数就是类别的个数 这意味着模型输出的维度就是类别的个数 接下来就是设计损失函数,计算模型输出的向量与表示类别的one hot向量之间的差异 代码示例
import torch
torch.eye(2)
tensor([[1., 0.],
[0., 1.]])
def one_hot_coding(class_num,index):
E = torch.eye(class_num)
return E[index]
one_hot_coding(class_num=2,index=0)
tensor([1., 0.])
|
模型输出本是连续的数值,是后续处理将之转化为了概率 严格来说,转化概率这一步,并不归模型管, 模型负责线性维度变换+激活函数 转概率这一步,完全可以在模型之外做 向量转概率 模型输出转概率,通常用softmax import torch p = torch.tensor([0.9,0.1]) torch.exp(p)/torch.exp(p).sum() + 1e-6 tensor([0.6900, 0.3100]) 对于[0.9,0.1],softmax明显不合理的地方 - 自然的思路,期望转化为概率后应该是90%,10% - 而softmax转化为的概率为[0.6900, 0.3100] - 这合理吗? 这是因为没考虑负数... softmax实际上是将数据拉到指数e的层面做了概率, 不管正负,经过指数运算后,皆为正,这符合了概率皆大于0的特点 其他概率
def v2p(p):
p_min = p.min()
p_max = p.max()
p = (p - p_min+1e-6)/(p_max-p_min+1e-6)
return p
p = v2p(p)
p
tensor([1.0000e+00, 1.2500e-06])
通常的就是sotmax,这是个人感觉也还可以的概率计算方式 - 但要注意这并不是严格意义上的概率 - 和并不为1 - 但模型通常要的是那个最大概率的值,其他的不为1好像也没关系 - 具体如何还需要验证... |
交叉熵可以求两个向量之前的差异,它来自于KL离散的概念
简单过一下概率的概念
- 这里标签已全部转化为概率
- 模型输出本是随机的连续值,这里也已转化为概率
- 两个都已是概率,那么就可以套KL离散的概念了
标签 y=[1,0]
模型 p=[0.9,0.1]
求这两个向量之间的差异/损失,实际上分两步
- 求向量每个维度上两个元素之间的差异
- 求和,各个维度上差异的和才是两个向量,也叫两个分布之间的损失
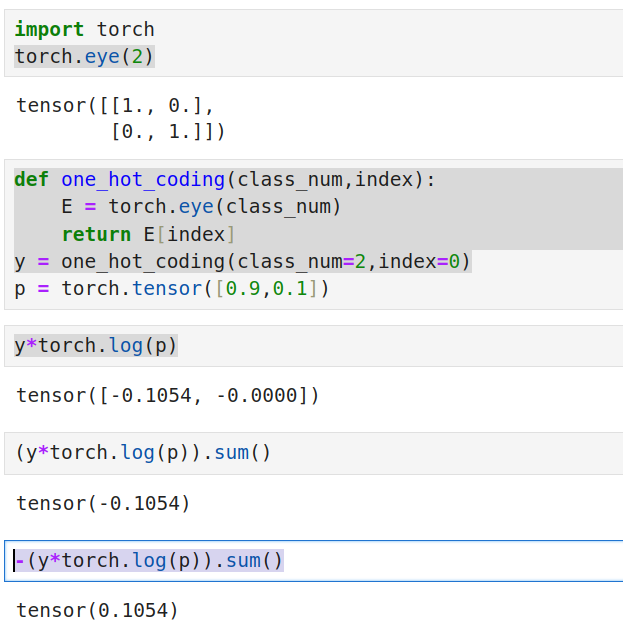
交叉熵公式 = -sum(y*log(x)) - y已转化为one hot向量 - x已转化为概率
-torch.log(p[0])
tensor(0.1054)
在标签已经化为One Hot向量的前提下
- 损失函数可以简化为 -torch.log(x_max)
- 即只计算 one hot向量1所在索引位置上样本x对应值的 log 即可
|
|
|
|
|
线性变换到向量
使用one hot标签 标识类别,那么模型就设计为将样本的维度变换到one hot向量的维度
损失函数 计算两个向量之间的差异
优化器使用梯度下降法 更新参数
这么强调,意在说明,如果标签不是one hot向量,比如其他维度都也有数据,
那么该流程依然适用,
因为标签向量如何映射回标签这个问题,并不归模型所管
只要在模型之外定义一个字典,
然后计算模型输出的结果向量离字典中哪个向量的距离最近,就能找到是哪个标签
|
import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
import torch
from torch import nn
from torch.nn import functional as F
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
# 加载数据集
X, y = load_breast_cancer(return_X_y=True)
# 切分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
print(X.shape,y.shape) # (569, 30) (569,)
# 数据预处理
mean_ = X_train.mean(axis=0)
std_ = X_train.std(axis=0)
X_train = (X_train - mean_) / std_
X_test = (X_test - mean_) / std_
class MyDataset(Dataset):
def __init__(self, X, y):
self.X = X
self.y = y
def __getitem__(self, idx):
x = self.X[idx]
y = self.y[idx]
return torch.tensor(data=x).float(), torch.tensor(data=y).long()
def __len__(self):
return len(self.X)
# 批量化打包数据
train_dataset = MyDataset(X=X_train, y=y_train)
train_dataloader = DataLoader(dataset=train_dataset,batch_size=32 ,shuffle=True)
test_dataset = MyDataset(X=X_test, y=y_test)
test_dataloader = DataLoader(dataset=test_dataset,batch_size=32 ,shuffle=False)
# 定义模型
class Model(nn.Module):
def __init__(self, in_features=30, out_features=2):
super(Model, self).__init__()
self.linear1 = nn.Linear(in_features=in_features, out_features=256)
self.linear2 = nn.Linear(in_features=256, out_features=out_features)
def forward(self, x):
h = self.linear1(x)
h = torch.relu(h)
out = self.linear2(h)
return out
# 构建模型
model = Model(in_features=30, out_features=2)
# 损失函数
loss_fn = nn.CrossEntropyLoss()
# 优化器
optimizer = torch.optim.Adam(params=model.parameters(), lr=1e-2)
# 过程监控
def get_loss(dataloader, model=model, loss_fn=loss_fn):
losses = []
with torch.no_grad():
for X, y in dataloader:
y_pred = model(X)
loss = loss_fn(y_pred, y)
losses.append(loss.item())
return np.array(losses).mean()
# 计算准确率
def get_acc(dataloader=test_dataloader, model=model):
accs = []
with torch.no_grad():
for X, y in dataloader:
# 原始输出,这是连续的数值,并没有转概率
y_pred = model(X)
# 类别转换,求数值最大的索引位置,对应标签类别
y_pred = y_pred.argmax(dim=1)
# 准确率的计算
acc = (y == y_pred).float().mean()
accs.append(acc.item())
return round(np.array(accs).mean(), ndigits=3)
# 训练函数
def train(dataloader=train_dataloader, model=model, loss_fn=loss_fn, optimizer=optimizer, epochs=100):
for epoch in range(1, epochs+1):
for X, y in dataloader:
# 正向传播
y_pred = model(X)
# 计算损失
loss = loss_fn(y_pred, y)
# 梯度清空
optimizer.zero_grad()
# 反向传播
loss.backward()
# 更新参数
optimizer.step()
print(f"Epoch: {epoch}, Train Acc: {get_acc(dataloader=train_dataloader)}, Test Acc: {get_acc(dataloader=test_dataloader)}")
train()
|
|
|
|
|
|
|
参考