二分类混淆矩阵
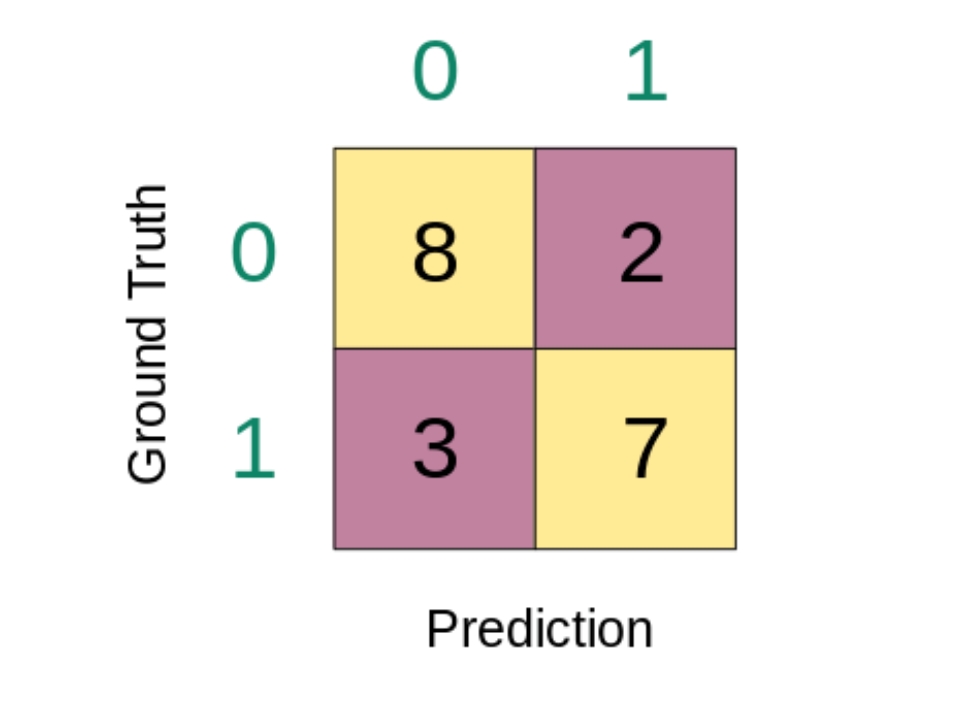
只区分 0 或 1。
它的行代表真实的类别,列代表预测的类别。
以第一行为例,真正的类别标签是 0,
有 8 个实例被预测为了 0,有 2 个实例被预测为了 1。
也就是说,在这 10 个真实标签为 0 实例中,有 8 个被正确分类,有 2 个被错误分类。
第二行这 10 个真实标签为 1 的实例中,3 个预测错了,7个预测对了。
https://cloud.tencent.com/developer/article/1935919
https://zhuanlan.zhihu.com/p/436195289
|
|
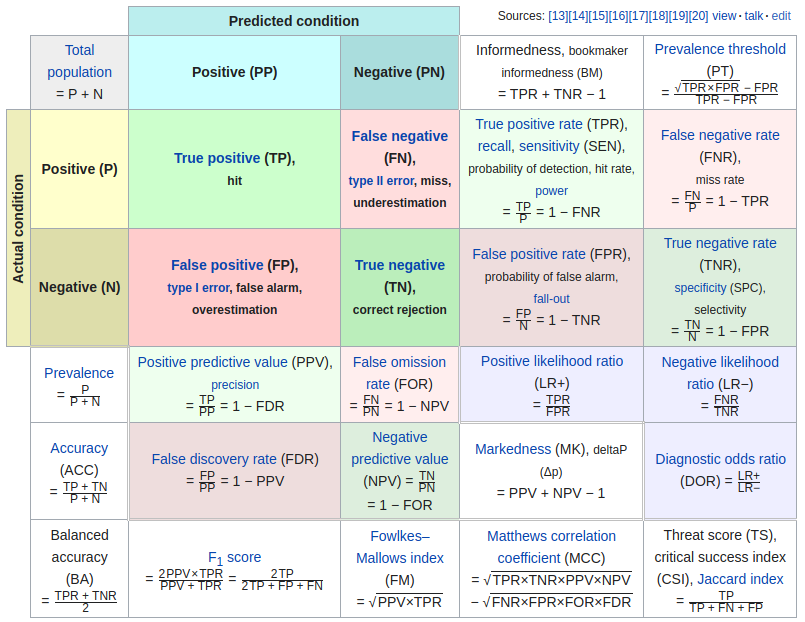
召回率(Recall): 召回率衡量了分类模型 正确预测为正例的样本数量 占 所有实际正例样本数量的比例。 
计算公式为: 召回率 = TP / (TP + FN), 其中 TP表示真正例(True Positive), FN表示假反例(False Negative)。 召回率越高,表示模型能够更好地捕捉到正例样本。 |
查准率(Precision): 查准率衡量了分类模型预测为正例的样本中真正为正例的比例。 
计算公式为: 查准率 = TP / (TP + FP), 其中 TP表示真正例(True Positive), FP表示假正例(False Positive)。 查准率越高,表示模型预测为正例的样本中真正为正例的比例越高。 |
F-度量(F-Measure): F-度量综合考虑了召回率和查准率,是召回率和查准率的调和平均值。 
计算公式为: F-度量 = 2 * (查准率 * 召回率) / (查准率 + 召回率)。 F-度量综合了召回率和查准率的优势,能够更全面地评估分类模型的性能。 |
|
|
生成混淆矩阵
|
sklearn
from sklearn.metrics import confusion_matrix
# 输出混淆矩阵
print("Confusion Matrix:")
confusion_matrix(y_test, pred)
Confusion Matrix:
array([[5494, 0],
[ 2, 47]])
pandas
pd.crosstab(y_test, pred, rownames=['Actual'], colnames=['Predicted'])
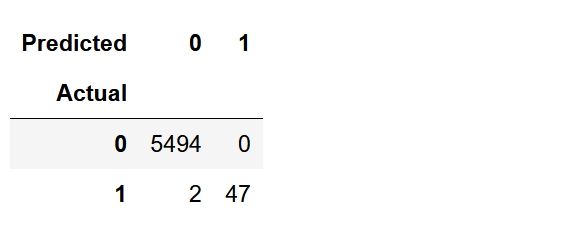
|
|
|
|
|
|
|
|
准确率
|
预测正确的数量占总数的比例
import numpy as np
np.random.seed(73)
y_pred=np.random.randint(low=0,high=2,size=(10))
y_test=np.random.randint(low=0,high=2,size=(10))
acc = (y_pred==y_test).mean()
acc = np.round(acc,decimals=4)
acc
等价于 == 转化为 true/false后的均值
---------------------------------------------------------------------
|
|
|
|
|
|
|
|
AUC
from sklearn.metrics import accuracy_score,roc_auc_score, confusion_matrix, classification_report, roc_curve, auc,f1_scor
# 预测测试集
y_pred = model.predict(X_test)
y_pred
array([1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1,
0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1,
1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1,
0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0,
1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1,
0, 1, 0, 0])
roc_auc_score(y_test, y_pred) # 0.9464461185718965 |
from sklearn.metrics import accuracy_score,roc_auc_score, confusion_matrix, classification_report, roc_curve, auc,f1_score y_scores = model.predict_proba(X_test)[:, 1] # 获取预测为恶性的概率 fpr, tpr, thresholds = roc_curve(y_test, y_scores) roc_auc = auc(fpr, tpr) roc_auc # 0.9977071732721913 |
|
分析差异的原因
阈值选择:
第一种方法依赖于一个固定的阈值(通常是0.5)来将概率转换为分类标签。
这个阈值可能不是最优的,导致分类性能不是最佳的。
信息利用:
第二种方法利用了完整的概率分布信息,
通过计算不同阈值下的FPR和TPR来绘制ROC曲线,并计算AUC。
这种方法通常更准确地反映了模型的性能。
哪种方法更准确? 在大多数情况下, 第二种方法(使用概率预测和 roc_curve、auc 函数)更准确地反映了模型的性能。 这是因为这种方法没有将概率预测简单地二值化为分类标签, 而是利用了模型输出的全部信息。 可能的解释 第一种方法可能由于选择了不合适的阈值(例如默认的0.5)而导致AUC值较低。 第二种方法通过考虑所有可能的阈值来全面评估模型性能,因此通常更可靠。 |
|
|
|
|
综合计算
精确率 准确率 召回率 auc F1 值
|
|
|
|
|
|
|
|
参考