无穷小与极限思想
现实世界中任意给定一个正数m,
那么用m除以10 或 1W...,就可以得到一个比m更小的数
所以,如果一个数给定了,那么总可以找到比它更小的数
并且可以没完没了地进行下去... 前提是数给定了
现在我们不定下这个数,而是以概念/抽象的形式描述,定下无穷小的性质,
1. 无穷小是描述数相关的一个量,类似y=x一样,x可以取各种不同的值,但x对应一个数,并且y=x是一个一元一次线性方程
2. 无穷小不是一个确定的数,而是描述一种数的变化,即你任意给定一个正数m,它都会比m小
3. 无穷小是大于0的,是正的
4. 对于任意给定的正数m,它与0之间都存在着一个无穷小(这样一个概念/逻辑存在)
5. 在非负数中,0是唯一比无穷小还要小的数,
注意哈,既然都唯一了,说明0与无穷小之间没有其他确定的正数了
无穷小的现实意义
无穷小到底有多小? 任意给定的正数m,除以这个宇宙所有原子的个数,除上10W次,这样一个数算是无穷小吗? 不算,因为它给定了,还可以接着除... 无穷小描述的是无限逼近0的一种趋势,是一种无穷无尽逼近的状态... 这种状态还有另外一个名字,就是 极限 极限,用于描述一种极致的状态 极致到什么程度呢?就是 唯 一 (这里约定是线性维度,即1维/1阶,y=x这个维度 上确定的数,即指0,无穷小的极限是0) 由于无穷小是逼近0的,这里的 唯一 就是指:没有任何一个给定的正数能比无穷小更接近0 这也是极限的思想:什么叫 极? 唯 一 便是 极 通过无穷小,引出了极限的概念 这里的唯一指在非负数范围内, 对于任何一个可以确定的非负数,0是最接近无穷小的确定的数 其对于任何一个确定的正数,都比无穷小大 0是可以确定的非负数中 “唯一” 最接近无穷小的数
为何要反复强调“确定”
这是为了限制范围,就“数”而言,它在数轴上并不是连续的, 有无限循环小数,还有无限不循环小数, 比如圆周率,3.1415926... 尽管尚不能确定它有多长,但不防给它一个名字,定下它的概念,描述/研究 它的性质 这里的确定更确切指现实中的确切,可以对应实物 也许,在虚的范围里,比如纯逻辑上的比较,也许圆周率可以无限延伸下去, 但在现实中,可能只需要前100位,就能解决N多的实际问题了 又比如无穷小这个数,前面特意提到y=x,实际上就是在说x*x有二次型, 那么无穷小也可以有平方,这是高阶无穷小, 这是纯逻辑上的运算/比较/结构, 在现实中,可能小数点后10位的数就能解决很多问题了,并不需要它一直小下去 这是一种逻辑上的 概念/形式/存在
没有任何一个给定的正数能比无穷小更接近0
无穷小实际上描述的是一种状态, 无限小的一种状态(其实正负只是数的其中一个维度), 从正的方向无限逼近0的一种状态,一种极限的变化趋势 无穷小不是一个确定的数值
在正数的范围内,有没有比无穷小还要小的存在?
有
无穷小不是确定的数值,所以这个存在也不是确定的数
但无穷小是线性的,一如 y = x一样,x是个变量,自变量,x可以是1,2,3,...
无穷小是一种状态,一种趋势,同样可以用一个符号来表示
无穷小符号通常用小写希腊字母表示,如α、β、ε等,
有时候也用α(x)、ο(x)等,表示无穷小量是以x为自变量的函数。
以α表示无穷小,那么α×α,即α的2次方,就是比α高一阶的无穷小
α的2次方就是比α更小的存在,但它同样不是确定的数值,也是一种变化趋势
简言之,没有比无穷小更小的(确定的)正数,
但有比无穷小更接近0的状态/存在,那就是它自己的高阶形式
前面有提到,极限之极就在于唯一,但这是有范围的,
这个范围/提前就是“确定的非负数”,在这个范围下,0就是那个唯一
无穷小以及基于它自身的高阶无穷小,则不在这个范围内,所以并不与极限的唯一冲突
其实,极限在定义时,必会说明其定义域,这个域就是范围
在这一个什么样的范围里,是唯一的!
精确的 范围,经过N次验证的 逻辑,这正是数学能做到精准的根源,为数学之本 其实,在讨论中发现有冲突的观点/现象时, 逆向思考这些观点的范围是不是大了/偏了/错位了, 一经思考,冲突自消...
极限的定义
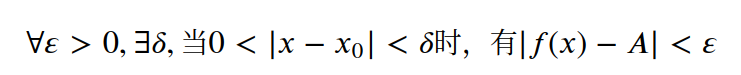
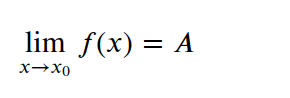
对于任意给定的正数𝜀,总存在正数𝛿,使得当0 < |x - x0| < 𝛿时,|f(x) - A| < 𝜀 即当x趋于x0时,f(x)趋于常数A (这里特意强调了A是常数,目的在于说A是一个确定数值)
去心邻域
x趋于x0,但x不等于x0,是无限接近x0,但不要求x=x0 即允许f(x)的定义域不包含x0这个值
变量及其变化
使用变量描述数据变化的规律
用变量表示变化的数,通常使用符号,a,b,c,x,y,z,w等等 以x为例,可以表示一系列的数,定下这个基调之后,就可以进一步引入更多的内容 - 2x表示的数是x的两2倍,虽然有些废话,但要在脑海构画出这样一幅情景: - 一系列数据在变化,而另外一系列数据与该系列的数据变化规律差不多,但幅度比较大; - 但总体上它们的曲线变化趋势近似/同比 - 为了更好地研究2x与x的变化规律,引入坐标系 - y1 = 2x ,y2 = x - 在解析几何的图形中,可以看到y1(就是2x)是y2(x)的两倍大小 y = ax + b = f(x),f(x)中的x通常称为自变量, x经过f(x)=ax+b 这样一个结构之后,得到新的变量y,这个变量y 叫 因变量 同样是变化,f(x)的结构不一样,因变量y随x的变化规律也不一样
变化的比值/变化率
什么是变化 - x - x0 可以表示一个变化,对应y的变化是y - y0 - x变量本身是变化吗? 不是 - x是变量,代表的是一系列的数,可以呈现一个数据分布,可以描述该分布的规律 - 但x不是变化,x-x0 才是变化 变化的比值 - 两点确定一条直线,以x0表示一个定点,x表示直线上其他任一点 - y - y0 = k(x - x0) 就可以表示这条直接 - (y - y0)/(x - x0) 就可以描述变化的比值 k - 虽然变化是不定的,但依然有其规律,有其不变的事物 -
变量的阶数
阶数: 这里的变化是指自变量x对应的因变量y的变化,以y=f(x)为例 , 如果其变化是一个常数,即y-y0=f(x+x0)-f(x)=a(x+x0)+b-(ax+b)=a*x0(其中a*x0是个常数),则变量y是一阶变量 如果其变化是一阶变量,即y-y0=f(x+x0)-f(x)=(x+x0)(x+x0)-x*x=2x*x0 + x0*x0,则变量y是二阶变量 ... x的0阶是1,y = ax + b实际上是y=ax + b*x的0次方,这里面有0阶,1阶, 自然会问,会不会有二阶与三阶,就是下面这样的 y = a0*x的0阶 + a1*x的1阶 + a2*x的2阶 + a3*x的3阶 + ... + an *x的n阶 这是单个变量在各个阶数上的展开,描述了单个变量的N多变化, 实际上x的2阶,就是x*x,可以使用x + x + ... 直到x个x相加得到, 乘法的本质还是加法, 上面的按阶展开,某种程度上等价于 y = w0 + w1*x + ... + wn*x 区别是速度与效率... 也就是说,低阶运算使用等价的高阶运算来实现,速度要快上很多
变化中不变的部分
(y - y0)/(x - x0) = k 这个k就是不变的部分 y = ax + b = f(x), f(x)代表不变的结构 这个不变的结构,也就是函数,是变化中不变的部分, 通常更看中同阶的变化率k 变化的事物不定,重点研究的是其中不变的部分
因变量的导数
y=f(x)可导
当△x->0时,△y/△x的极限存在,则y=f(x)可导 y = f(x) = ax + b 是一个变量,因x变化而变化的量, y的变化/x的变化 = △y/△x = (y - y0)/(x - x0) = a 由此可见,函数y=f(x)的导数就是 y的变化/x的变化, 其结果是比f(x)低一阶的另外一个函数g(x) 常数的导数是0,即常数没有变化 y=f(x) = ax + b一阶函数的导数就是 常数 y=f(x)二阶函数的导数就是 x的 一阶函数 y=f(x)n阶函数的导数就是 x的 n-1 阶函数 当y=f(x)的阶数n大于或等于2时, △y = f(x+△x) - f(x),消去了x的最高次冥及常数项,剩下的是△x从1阶到n阶的展开, △y/△x = y的导函数g(x) + 𝛼(无穷小)(当△x->0时) 其中𝛼是a1*△x的一次方 + a2*△x的二次方 +...+ (an-1)*△x的n-1次方展开, y的导函数g(x)就是 f(x+△x)展开后 △x一次方的系数, 其他系数由于△x存在,在△x->0时,趋于无穷小其极限归于0了
因变量的微分
dy是△y的线性主部
△y/△x = y的导函数g(x) + a1*△x的一次方 + a2*△x的二次方 +...+ (an-1)*△x的n-1次方 △y = a0*△x + a1*△x的2次方 + a2*△x的3次方 +...+ (an)*△x的n次方 当△x->0时,△x的2次方及后面的△x的n次方 是比△x更高阶的无穷小, 此时,△y 近似于 a0*△x, a0*△x 就是y=f(x)的微分,记作 dy 当y=f(x)是1次函数时,比如y=ax+b时,△y = dy + 0 当y=f(x)的次数大于等于2时, △y = dy + o(△x) 其中,o(△x) 是△x高阶无穷小的展开
dy是f(x)导函数的分母
y = f(x) f(x)的导函数 = dy/dx 在自变量x这个维度,dx就是△x,即dx=△x
微分思想
首先,我们看到的是一个函数y=f(x) ,这个函数对应一个图像 比如,y=x*x,这是一个曲线, 然后是,入微,怎么进入“微”的视觉呢,或者说怎么分才叫“微...分”呢? 微分dy是△y线性主部,△x是共用的,是一样的 也就是说,将x分为一个个△x的时候,y=f(x)对应的△y 近似于 一个直线y=ax+b中△x对应的△y2(也就是dy) 直线y=ax+b与y=f(x)在△x范围内相交,它们的△y近似,并且前者是后者的微分 微分是一种什么样的分法呢? 是一种 微小的区域 的线性分法, 是将函数y=f(x)用无数多个y=ax+b的 微小线段 表示的方法 其中a是y=f(x)在x处的导函数 微分意在强调将 一个事物 分解成 无数多个 微小的线段,是一种线性分法
定积分
微分回顾
微分dy是△y的线性主部,当△x->0时,△x的高阶部分可忽略 △y = a0*△x + a1*△x的2次方 + a2*△x的3次方 +...+ (an)*△x的n次方 当一系列△y相加时 △y1=y1-y0 △y2=y2-y1 △y3=y3-y2 ... △y1 + △y2 + △y3 + ... + △yn = yn - y0 ≈ w1*△x + w2*△x + w3*△x + ... + wn*△x = dy1 + dy2 + dy3 + ... + dyn 其中w1,w2,w3,...,wn是y=f(x)在相应x处的导数
积分思想
y=f(x)的导函数为y=g(x),那f(x)叫g(x)的原函数
逆向看微分的过程:
w1*△x + w2*△x + w3*△x + ... + wn*△x
≈ △y1 + △y2 + △y3 + ... + △yn = yn - y0
是一个由导函数y=g(x)到y=f(x)原函数的过程,
将导函数y=g(x)的x轴分成无数份,每一份为△x,
其中w1,w2,w3,...,wn是y=g(x)在相应x处的函数值,
wn*△x是一个 微小矩形,所有这些 微小矩形相加,就是积分
这里x指定区间,
即函数y=g(x)在指定区间[a,b]上的积分为 y=g(x)在x(其中x∈[a,b])上的定积分
“定”指x有区间,并非负无穷到正无穷,
一个函数在[a,b]区间上的定积分的结果是其原函数在[a,b]区间的差,即 f(b)-f(a)
不定积分
不定积分的定义
x的作用域是非负无穷到正无穷, 那 y=g(x)在x上的积分 就是不定积分 g(x)在x上的不定积分 = 原函数f(x) + 常数C
不定积分指什么
g(x)在x上的不定积分 = 原函数f(x) + 常数C 举例说明: 设原函数y=f(x) = ax + b , 导函数y=g(x)=a,在二维坐标系中就是一条直线, 在x轴上取一系列的△x, a*△x就是一系列的 微小矩形 这里为说明不定积分公式左右的关系,△x就不取微小的值了, 取1,2,3,...便于理解,同时对于导函数不变的直线来说也是等效的 在x轴上取1,2,3,... ,也就是说,△x = 1 每个矩阵的大小a*△x = a, 这里我们有两组变量,我们观察这两组变量之间的关系 函数y=g(x)=a, 在[0,1]的积分是a 在[0,2]的积分是a+a=2a ... 在[0,n]的积分是a+a+...+a=n*a 它们之间的关系不就是x与ax之间的关系吗! 所以,函数y=g(x)=a在x(x∈[-∞,+∞])上的积分就是ax , 即一个函数的不定积分就是其原函数的非常数项部分 我们将最开始的公式变换一下 原函数f(x) = g(x)在x上的不定积分 + 常数C 意思就是原函数与导函数的不定积分只差一个常数项C 最开始的定义,意在强调 积分 是由 导函数在x变量的维度上通过 微小矩形 累加/积累 得到的 原函数 如果将原函数看作两个部分,变化的部分+不变的部分,那么导函数的不定积分就是原函数中变化的部分
求导函数不定积分的原函数
实际上就是求一个函数的原函数 回忆一下微分,入眼首先是原函数, 我们要观察的是原函数的变化(实际上是低一维的变化,就是它的导函数的值), 微分的视角是用一个个 微小线段 替代原函数的曲线, 这些 微小线段的斜率 就是原函数在对应x处的导函数的值 而在积分中,入眼的是导函数,导函数在x处的值*[x,x+△x]得到的一系列的面积的累积, 这种累积的变化趋势就是原函数的变化趋势,其中的常数项不改变其曲线形状, 我们设F(x) = 原函数f(x) + 常数项C0,满足F(0)=0,即将y=f(x)上下移动一下,使之通过原点 由定积分的公式可知: 导函数y=g(x)在[0,x]上积分=F(x)-F(0)=F(x)-0=F(x) 从这个角度看,导函数在[0,x]上的积分, 即导函数曲线与x轴[0,x]范围形成的面积,就是原函数F(x)的值 按积分的定义,将[0,x]分成n个微小区间,g(x1)*△x + g(x2)*△x +...+ g(xn)*△x 就能得到F(x)的值 使用计算机暴力计算,可以得到一组(x,F(x))数组供人使用,但无法得到y = lnx + b 这种精准的数学表达式 高等数学的解决思路: 原函数求导得到导函数,这个过程可以精准计算, 根据历史经验得到一组组原函数与导函数的对应关系表, 比如,lnx的导函数=1/x,有了这个参照关系,那么1/x的原函数自然就是lnx + C 高等数学188页,原函数与导函数参照关系,共给出了13种, 包括了一元n次,三角函数,反三角函数,指数函数,对数函数 五大类,基本上覆盖了当前数学常用函数 这全吗?当然不...还有无数的未知函数等着人们去发现, lnx的低一级变化是1/x,那lnx的高一级变化,即lnx的原函数是什么,你知道吗?
参考