注意力取特征

 
以文本，句子，单词为例，
首先要定下一个单词的维度，即用多少个维度 (线性)表示/描述 一个单词，

此处设为n,即用 n个 有次序的 实数 线性表示 一个单词 

一句话有m个单词，向量组[m,n],也叫一个序列Seq[m,n]

某个单词word[1,n]相对一个序列的注意力：
[1,n]@[n,m]=[1,m]

向量组[m,n],向量组[n,m]都可以读作m个n维向量，它们对应的事物为同一事物
同样的，一个维数为n的向量，[1,2,...,n],(1,2,...,n)
横着写，竖着写，为行向量，还是列向量，用中括号写，小括号写，甚至不加括号
都是指的同一个单词，对应的为同一事物，同一数据，
改变形式是为了落地计算需要，真正可以在一起进行运算的，必须维数相同的事物/向量,
接上面的公式 [1,n]@[n,m]=[1,m] 继续... 

[1,n][n,1]这样的运算进行了m次，就得到了一个维数为m的向量，
[1,m]就是一个维度/长度为m的向量，该向量 针对/对应 一个句子，一个序列
或者对应一个样本的全体单词，具有上下文信息 

转为概率后，突出其重点，也就是所说的注意力，
让重要单词对应的数值大一些，不重要的趋于0 
考虑全体的同时，又突出重点，同时忽略末枝

一个序列[m,n]表示的是m个单词，每个单词n维，这是从行维度去看的，
也可以看作，n个 维数为m的列向量 形成的向量组，这是从列的维度去看的

从列的维度上看，
将维数为m的概率向量与序列中维数为m的向量进行向量内积运算，
即都是来自 单词元素维度(多少个单词) 的两个向量进行内积运算，进行融合，得到一个数值
这样的列有n个，于是得到一个n维向量 
这个n维向量就是一个单词关于一个句子的上下文向量 

先是在一个单词的n维向量这个维度上计算m次(序列转置一下)，得到一个m维向量
再从序列一个列向量有m维这个维度计算n次，又回到n维向量

 
整个过程就是经过了序列维度，单词维度的转化，最后约定还是转化为单词维度
最后得到的单词维度的向量 即包含整个序列的上下文信息，又突出了重点 

同时序列维度上还有顺序，即位置的信息，
比如第3个单词重要，那么第3个单词的得分/概率就会大
即注意力，包含整个序列的上下文信息，突出了重点，还包含有位置信息 

卷积取特征

 
注意力计算是全连接，所有数据，参数同时计算
卷积是局部分批计算，一次计算一个核

卷积计算无位置顺序，所有核计算完后相加，交互两个核的位置对加法计算结果无影响 

卷积也无上下文信息，
- 这么说并不准确，毕竟卷积每次计算的结果涉及了全部数据
- 说到上下文信息，更多的是指序列位置，局部与整体的依赖关系，
- 卷积是涉及所有数据了，但它没有重点，一视同仁，全靠损失函数逼迫 

卷积同样可以分层，即将不同的信息分于不同的层上，但这不是求相对比例/概率 
这是靠损失函数的逼迫才完成的 

论效率，理论上卷积高一些(这么说是因为本人没有对此观点进行研究论证，但多次听说有一些项目用了卷积提升了效率)，
毕竟它需要的资源上限不高，一次只是计算一个局部
    

维度的约定

 
注意力维度约定：
单词/元素 特征维度 -- 序列维度 -- 单词元素 特征维度


卷积维度约定：
先将单词/元素 特征维度 从小变大，再从大变小，


卷积这个约定是从大量实践总结出来的 
注意力的这个维度约定更多由数据的性质决定，
而卷积最开始处理的是图像，很难从图像中总结出序列相关的性质 

做NLP的去数一数一句话有多少个单词是一件很自然的事，
做CV的难道要去数一数一个图像有多少个像素吗，
毕竟一个像素没有一个单词有那么丰富的含义... 
    

 
当然了，从技术的角度，这么做完全没问题的
因为像素之间的确有位置，只是你没有加入位置的处理技术
个人认为文本完全可以转图像，只需要分层转化一下
将几十万个单词划分为0-255个等级/类别/层次，每个类别用3个数值表示，
这就不就成图像了嘛（这段话仅个人推猜，尚未实验论证...）

RNN取特征

 
RNN专于序列，第t次计算完之后，才会进行第t+1次计算，
在时间上有前后依赖关系，所以RNN无法并行计算

卷积就可以并行计算，开两个线程，
一个线程计算前一半的核，一个线程计算后一半的核，最后结果相加 

RNN必须一个结果计算完后才能计算下一个结果，无法并行 

序列长度

 
RNN能处理一定的前后依赖，
这句话的潜台词是针对卷积的，因为卷积不能处理前后依赖关系

但缺点是无法处理序列过长的信息，一般不超过20个，超过10个交易就下降，
因为RNN是时间位置上前后依赖，离当前位置越远信息丢失越严重，

注意力突出了重点，并且这个重点跟当前单词的远近无关，
所以能处理更长的上下文信息 
    

 
在seq2seq2中使用RNN提取序列特征
- RNN是有前后依赖关系的，因此不能并行运算
- 注意力替换RNN后可以并行运算了，但不再有前后依赖关系了 

 
解决办法是 通过位置编码 加入 位置信息 
- 因为有了位置信息，相同的单词处于不同的位置上时，信息是不一样的 
- 位置编码数的数值不能太大，毕竟向量的值的范围为[-1,1]

Q 是查询， K 被查询， V 计算关系得分

 
QKV矩阵的shape是一致的 

Q与K矩阵相乘，从向量维度看就是向量内积，就是向量的乘法，
乘法在[0,1]这个范围内，更多意义是求共性，更专业的名称就是 相似度 

Q与K矩阵相乘 就是求Q中每元素相对K中每个向量的 相似度，重要程度，
经softmax化为百分比，这个百分比是谁的百分比？

是Q中每个元素相对K矩阵每个样本的百分比

    

 
张三，年净收入30万，买了个1万块苹果手机
李四，年收入3万，买了个1万块苹果手机

同样是“1万块苹果手机”，在张三和李四心中的份量是不一样的 
而softmax之后的百分比，仅是限于它们所在一句话的百分比

但矩阵数字化之后，哪些数字大，哪此数字小，已经是在统一的量纲上了，
句子之间已经隐含地有比较的意义了

为了让这种比较更有意义，让百分比脱离本句话，依然能与其他句子有横向比较的意义
将这个百分比矩阵与值矩阵V进行相乘 
同一句的百分比乘以本句话本身的值，得到一个相对整个辞职 具有横向比较意义的V值 
    

 
Q矩阵与K矩阵相乘，并不是直接乘法

而是与K矩阵的转置矩阵相乘，这一点是数学上的需要

这里QKV通常是一样的，这就转化为一个矩阵与自己相乘

比如A.shape=[3,5],矩阵A想与要自己相乘，从纯数学的角度，就必须对自身转置

[3,5]@[5,3]才可以 

    

 
Q矩阵与K矩阵的相乘也是如此 ，有时Q矩阵与K矩阵是同一矩阵，

至于要对谁进行转置，要看组成矩阵的向量的含义 

这里Q矩阵，就是进入神经网络的矩阵，通常用一个行向量表示一个样本 

即Q矩阵中的一行，就是一个样本，
与“Q矩阵的转置矩阵(行变成了列) ”中的一列(还是原来的一行)，
即Q矩阵的一行，还是那个样本，进行了向量内积运算，
转来转去，矩阵只是一个形式，一种计算方式，实际是样本向量与样本向量自己的内积运算，
求的是相似度，重要程度

这样从业务的角度也是说得通的，
所以不管是从业务还是数学角度，实现计算时，Q矩阵是与K的转置矩阵相乘的

 
梯度怎么算不稳定？
在AI的神经网络中，梯度爆炸指梯度比较大，
这样梯度下降法公式 w=w-0.001*(w的梯度) 计算时，变动就比较大，就不稳定
换句话，梯度小一点，就稳定一点 

这里Q与K的转置矩阵相乘后，其本质是，两个样本向量的内积运算，
样本向量各个维度相乘再相加，如果样本向量的维度比较大，
比如GPT大模型中一个向量的长度高达10万以上，
那么就是10万以上个数值 相乘再相加，得到的元素值就有可能比较大 

这就导致，向量维度一大，元素值就普遍变大，
这让AI神经网络计算起来不方便了，数大，容易爆炸

y1=2x
y2=10x 
y1*y2分别求梯度后相乘，结果为2*10=20，如果前面加个分数系统的数，
比如1/2，那这个梯度结果就变成为20/2=10，梯度变小了 

向量维度大，可以有更丰富强大的表征能力，
因此，除以一个与向量维度相关的数值，以减弱这种维度变大带来的不利影响，
这里这个数值采用的是 向量维度的开平方根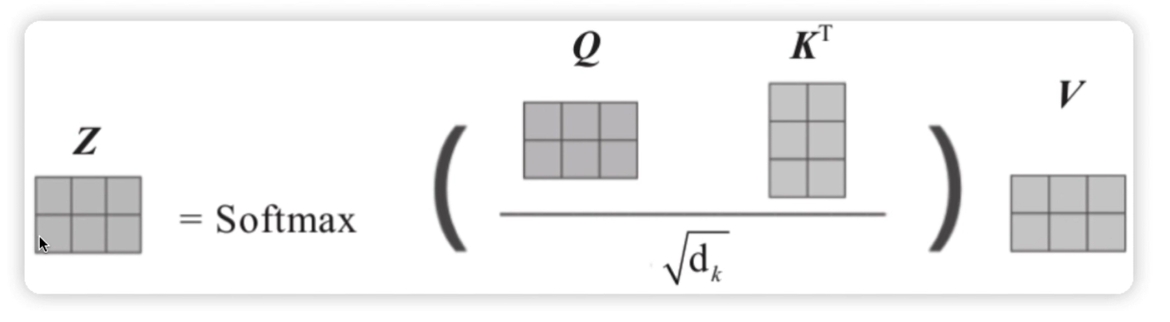 

 
向量的维度/头的个数 
头的个数，比如，4，8 

可以并行计算 

原来计算的最小单位是，样本向量与样本向量的内积，
是样本向量全体元素与另外一个向量全体元素的整合/融合 

多头，比如4，是将一个样本向量拆分为四份，这四份可以并行计算，
各自融合各自对应部分的信息

 
用[色泽，味道，价格，营养价值，大小，重量，保鲜时长，购买方便程度]来表征人对水果的喜爱

多头就是，
[色泽，味道]一起算然后整合，
[价格，营养价值]一起 
[大小，重量]一起 
[保鲜时长，购买方便程度]一起 

原来的向量内积就是所有维度相乘相加，多头则是单个的部分进行内积运算，
《注意力就是一切》这篇论文的作者说多头注意力的计算方式更好一些