卷积数据格式
1维卷积
文本 [B,C,L]
2维卷积
[B,C,W,H]
C
C:是特征维数,是通道channel ,一个特征向量有多少个维度,用多少个数表示一个特征向量 data.shape= [B,C,L] data[0]为一个元素 用多少个维度/什么样的shape去表示一个业务元素/自然元素 - 文本,一句话L个单词 - 图形,[w,h]个像素 - 这是shape,是形状, 每个业务元素/自然元素 再赋予不同的含义 - 比如,图像的像素,可以用一个向量去表示,特征维度为3,特征数为3 - 每个单词也可以用一个向量去表示
卷积计算的是特征维度,是所有数据shape上特征维度的线性组合,因此不改变shape
图像,以像素为自然元素,每个像素使用RGB三色表示
- [w,h]个像素形成一个图像,每个像素使用三个数来表示
- 用卷积计算,其数据shape为[B,C,W,H] = [B,3,W,H]
文本
- 一句本有L个单词,每个单词用embedding_dim个数来表示
- 用卷积计算,其数据shape为[B,C,N] = [B,embedding_dim,N]
交易
- 库表中的一行交易有N个列,每个列有一个业务含义,可用一个向量来表示
- 通常这个向量就是一个数,
- 用卷积计算,其数据shape为[B,C,N] = [B,1,N]
卷积常用参数
nn.Conv1d(
in_channels: int,
out_channels: int,
kernel_size: Union[int, Tuple[int]],
stride: Union[int, Tuple[int]] = 1,
padding: Union[str, int, Tuple[int]] = 0,
dilation: Union[int, Tuple[int]] = 1,
groups: int = 1,
bias: bool = True,
padding_mode: str = 'zeros',
device=None,
dtype=None,
) -> None
重要参数 in_channels: int, out_channels: int, kernel_size: Union[int, Tuple[int]], stride: Union[int, Tuple[int]] = 1, padding: Union[str, int, Tuple[int]] = 0, |
import torch from torch import nn X = torch.randn(3,1,7) conv1 = nn.Conv1d(in_channels=1,out_channels=8,kernel_size=2) conv1(X).shape # torch.Size([3, 8, 6]) 特征的线性变换
特征从1变为8,从8个维度去看这份数据,就产生了8个结果
特征shape从7变了6,少了1
stride: Union[int, Tuple[int]] = 1,
padding: Union[str, int, Tuple[int]] = 0,
省略的参数,stride默认为1,padding为0(即不补)
此处K=2
(7 +2*0 - 2 )/1 + 1 = 6
即
(x +2*0 - 2 )/1 + 1 = x - 1
卷积后通常会跟一个maxpool来改变特征图,如果整张特征图取一个特征的话,就是 nn.MaxPool1d(kernel_size=x-1) |
|
|
|
|
|
nn.Conv2d 理论
官方API
https://pytorch.org/docs/stable/generated/torch.nn.Conv2d.html#torch.nn.Conv2d
调用示例
import torch from torch import nn torch.manual_seed(73) conv2d = nn.Conv2d(in_channels=3, out_channels=32, kernel_size=(3, 3), padding=(1, 1), stride=(1, 1)) k=3,p=1,s=1这种 3 1 1的设计可保证特征图形状不变 (L + 2*1 - 3 )/ 1 +1 = L -K是减掉了第0步,即移动之前占的那个位置,所以最后+1,把这个补回来
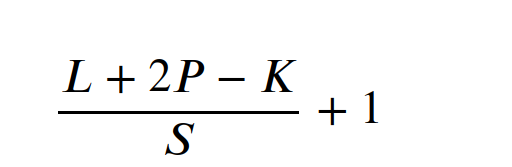
pytorch图像输入的格式[N,C,H,W]
# [N, C, H, W] # N:batch_size # C:通道数/特征层 # H:高度 # W:宽度 X = torch.randn(32, 3, 512, 256) X.shape torch.Size([32, 3, 512, 256])
卷积变换的是特征层数(前提是311设计)
比如,最初一个像素特征有3个维数,即RGB三色, 可以使用卷积将这个像素的特征层数提升到32,即使用32个维度的数据来表示这个像素 conv2d(X).shape torch.Size([32, 32, 512, 256]) out_channels=32,因此得到32个新的特征层, 每个特征层都是原来3个特征层的整合,是对原3层特征图整体数据 某个维度的 提取/一次计算 因为提取了32次,所以才得到32个特征层
批次的维度永远不变
一个样本对应一个结果,永远是一对一,所以批次的维度在计算的过程中永远不变 conv1 = nn.Conv2d(in_channels=3, out_channels=32, kernel_size=3, padding=1, stride=1) imgs = torch.randn(64, 3, 512, 512) conv1(imgs).shape torch.Size([64, 32, 512, 512])
非311的设计就会改变特征图shape
conv2 = nn.Conv2d(in_channels=5, out_channels=30, kernel_size=(3, 5), padding=1, stride=2) imgs = torch.randn(32, 5, 5, 5) conv2(imgs).shape torch.Size([32, 30, 3, 2]) 5 + 2*1 - 3 = 4; 4 /2 = 2; 2+1=3 5 + 2*1 - 5 = 2; 2 /2 = 1; 1+1=2
参数:偏置b
b = conv2.state_dict()["bias"]
b
tensor([ 1.1633e-02, 8.4127e-02, -2.0785e-02, 3.5110e-02, 1.0957e-01,
8.1714e-02, 7.5002e-02, -1.0953e-01, 3.1369e-02, -3.4423e-02,
1.9286e-02, -9.6399e-02, 4.3017e-02, -3.2373e-02, 1.2796e-02,
8.5092e-02, 7.9171e-02, 5.7777e-02, -9.4634e-02, 1.0043e-01,
-6.0957e-02, 4.0399e-02, -2.4609e-05, -8.7420e-02, -9.3181e-03,
-6.8756e-02, 9.5733e-02, -4.2755e-02, 5.5806e-02, 1.0345e-01])
b是一个向量,维数有30个,
卷积输出了30次,每次计算对应一个偏置,
毕竟每次输出对应的维度不同,偏置通常也不会一样
人各有志,世界上没有相同的两片树叶,
肯定是因为有不一样的因素在影响,每个树叶变化的方向会有所差异
参数w
w = conv2.state_dict()["weight"] w.shape torch.Size([30, 5, 3, 5]) 30是批次 5是特征层数,是原数据的特征层数,因为w是要 与"原数据"进行运算的 [3,5]是w的shape,原数据核kernel_size=(3, 5),所以w.shape=[3,5], 注意这里不是矩阵乘法,是按位相乘再相加, 即卷积的最小计算单元是按位相乘再相加
nn.Conv2d 计算举例
新维度上的一个数值outj = 各个特征层C上的“参数矩阵与对应核矩阵相乘再相加”之后的总和 + 偏置j
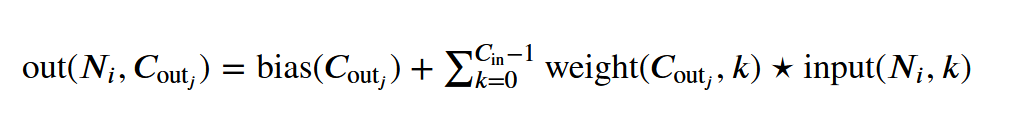
Cout 输出的维度 N 批次 Ni 批次中第i个样本 Cin 输入的维度,特征层,比如图像中的RGB三色,就是3,每个颜色使用相同的一个参数矩阵,三层共享一个偏置 Cout 输出的维度 bias 每个输出对应一个偏置
卷积计算公式数据及参数准备,参数就借用一下nn.Conv2d随机生成的参数,关键看计算过程
import torch from torch import nn torch.manual_seed(73) X = torch.randn(1, 3, 3, 3) conv2d = nn.Conv2d(in_channels=3, out_channels=2, kernel_size=(3, 3), padding=(1, 1), stride=(1, 1)) w=conv2d.state_dict()['weight'] b=conv2d.state_dict()['bias'] print(w.shape, b.shape) # torch.Size([2, 3, 3, 3]) torch.Size([2])
卷积计算过程分析
torch.sum(X[0,0,:3,:3]*w[0,0,:,:]) + torch.sum(X[0,1,:3,:3]*w[0,1,:,:]) + torch.sum(X[0,2,:3,:3]*w[0,2,:,:]) + b[0]
X[0,0,:3,:3] 取第1个特征层上前三行与前三列,取出一个kernel_size=(3, 3)的[3,3]子矩阵,
如此才能与[3,3]的参数矩阵w,按位相乘再相加,
公式中那个大大的星号,代表的是按位相乘,sum将它们相加
X[0,0,:3,:3] 虽然是原始数据左上角第一个[3,3]的子矩阵,
但,这是没考虑补0的情况...
上下,左右,各补0,就是 padding=(1, 1)之后的结果是这样的
3+1+1=5
x = X[0,0]
a=torch.cat([torch.zeros(1,3),x,torch.zeros(1,3)],dim=0)
a
tensor([[ 0.0000, 0.0000, 0.0000],
[ 0.3408, 0.2297, 1.7066],
[ 1.3925, -0.2963, -0.0565],
[-0.6886, -1.2959, 1.1781],
[ 0.0000, 0.0000, 0.0000]])
a=torch.cat([torch.zeros(5,1),a,torch.zeros(5,1)],dim=1)
a
tensor([[ 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.3408, 0.2297, 1.7066, 0.0000],
[ 0.0000, 1.3925, -0.2963, -0.0565, 0.0000],
[ 0.0000, -0.6886, -1.2959, 1.1781, 0.0000],
[ 0.0000, 0.0000, 0.0000, 0.0000, 0.0000]])
X[0,0]
tensor([[ 0.3408, 0.2297, 1.7066],
[ 1.3925, -0.2963, -0.0565],
[-0.6886, -1.2959, 1.1781]])
x = X[0,0]只是取了X数据3个特征层的第1层,回到开头那个计算公式,
原始数据x相当于补完0后最中间的那个数据,所以
torch.sum(X[0,0,:3,:3]*w[0,0,:,:]) + torch.sum(X[0,1,:3,:3]*w[0,1,:,:]) + torch.sum(X[0,2,:3,:3]*w[0,2,:,:]) + b[0]
tensor(-0.6611)
的计算结果就是卷积计算[3,3]矩阵最中心位置的数值
验证
out=conv2d(X)
out.shape
torch.Size([1, 2, 3, 3])
1 批次的维度
2 输出维度为2
[3,3] 特征图shape,311核设计不改变原数据特征图shape
out
tensor([[[[ 0.3094, -0.0677, -0.1076],
[ 0.2938, -0.6611, -0.1007],
[ 0.3736, -0.3332, -0.4082]],
[[-0.2423, -0.2159, -0.4177],
[ 0.8199, -0.6038, -0.5338],
[-0.0077, 0.3984, 0.2478]]]], grad_fn=<ConvolutionBackward0>)
w.shape
torch.Size([2, 3, 3, 3])
2 输出维度,一个维度或者说一个新的层面,有一组参数矩阵;有几组输出就会有几组参数矩阵,每个输出都有一个参数矩阵
3 原数据特征层数,一层对应一组参数矩阵,
这里一组有3个[3,3]的参数矩阵,原数据每层对应一个[3,3]参数矩阵,3层共用一个偏置
[3,3]一个2维参数矩阵的shape
这里Cout(输出的维度)= 2 ,所以out有两个矩阵,
其中第1个矩阵就是参数矩阵[0,:,:,:]与原数据计算的结果
最中间的数据-0.6611,与公式计算结果相符
至此,验证完毕,虽然只验证了一个数,其计算过程都是一样的
nn.Conv2d 关键点
要点
一个n维向量有n维,这好像是废话... 这个n维,就是特征层,就是特征维度, 特征,特征层,这么抽象的事物,就是n维向量的n个维度, 每个维度上就都一个shape,只不过向量的shape为1, 如果shape高于1就是向量组/矩阵了,初学者应该以向量组的角度去看更容易理解一些 以RGB三色图像为例,再回忆一下上面的计算,从向量的角度看过去, 一个图像有shape[H,W]个3维向量组成,一个向量就是一个(R,G,B) 真正计算的最小单位是 sum(向量[R,G,B]*参数W[w1,w2,w3]) + 偏置b = 一个新的维度 细节在于卷积一次 计算一个核的(比如K=[3,3])个向量 一个图像有shape[H,W]个3维向量,格式就变成了 [C,H,W],再加上批次的维度就是[B,C,H,W] 实际上还是将一个n维向量转换到,或者是变换出 1,2,...,m个新维度,形成一个m维度向量 重点在于维度的变换,这也是后来的卷积使用311核,只变换维度,不改变shape的原因 就是为了强调,卷积的设计 为的就是/目的就是/现在专于 维度的变换(维度变换在AI角度就是提取特征)
卷积计算演示图
最后再来看看这张广为流传的卷积计算图
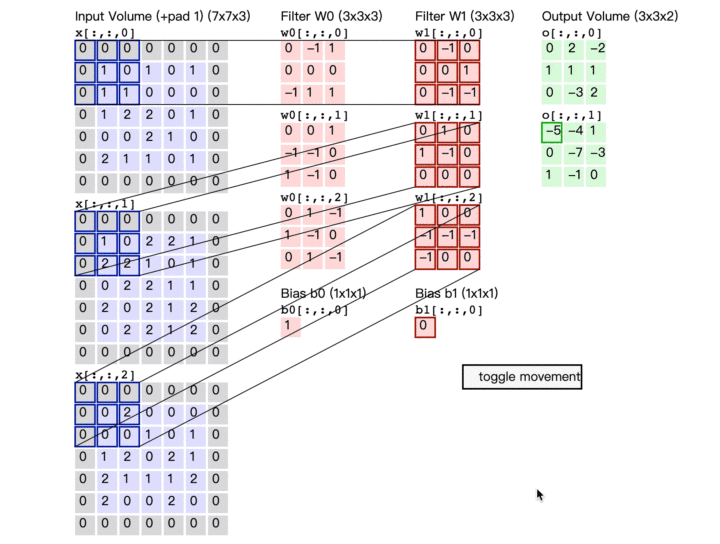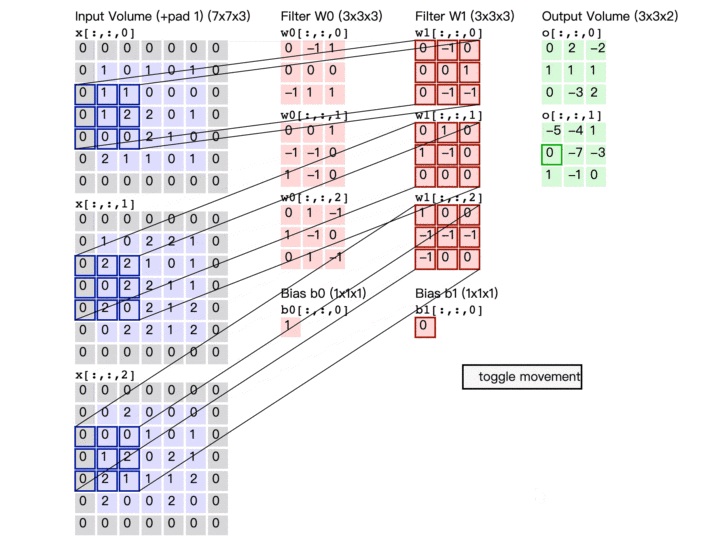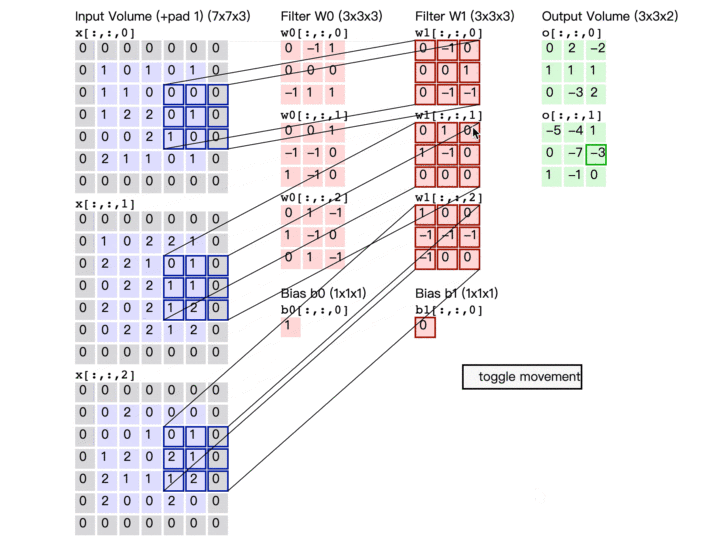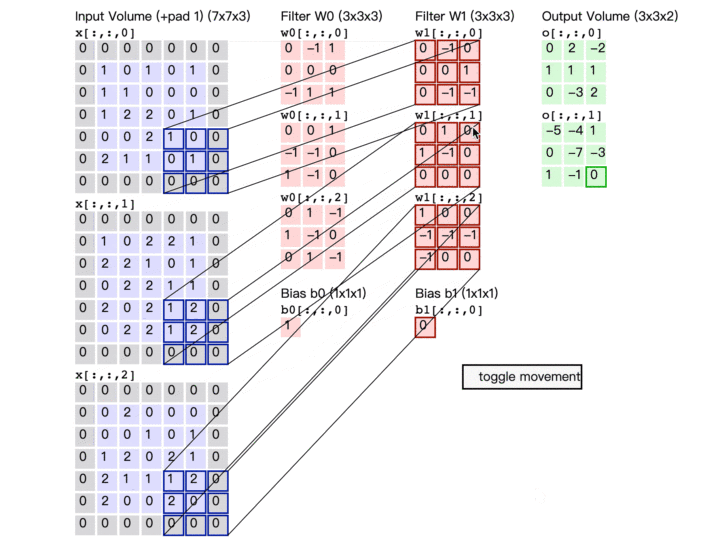
卷积参数量估计
输出特征数:每一个输出都是一次卷积计算的结果 一次卷积计算涉及参数量:输入特征数*卷积核大小 + 1个偏置 总参数量 = 输出特征数*(输入特征数*卷积核大小 + 1)
线性变换回顾
nn.Linear api
from torch import nn nn.Linear(in_features=13, out_features=2) Linear(in_features=13, out_features=2, bias=True)
nn.Linear 公式
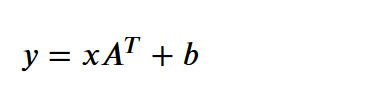
b=line.state_dict()['bias'] b tensor([0.0154, 0.0998]) 一个新的特征层上配一个单独的偏置 这里有输出二个层面,就有2个偏置 每个偏置与原数据所有特征层(向量的所有维度)进行加法运算 这与卷积一样,或者说卷层就是复杂点的全连接
卷积组件简述
卷积
提取特征,就是那个n维向量的维数,每一维都对应一个特征图(shape) - 通常是由少变多,比如RGB最开始有三个特征图,变32,64,256 - 多变少的工作后续由全连接完成
池化层
裁减特征图(舍弃不重要,保留重要特征) - 每一层上的特征图变小了,信息变少了 - 不是哪里都可以用的(它舍弃的信息有点多,有的场景效果不好),最终效果好不好要实践一下
批归一化BN
这里的归一化指(x-E)/std 按特征层对批数据进行归一化, 一个特征层/一个维度的数据进行归一化,不跨层,不跨特征 比如RGB,R颜色不会跟G颜色数据混合计算,各算各的 增加收敛速度
激活函数
ReLU PReLU 激活函数是非线性的,有可能提升模型拟合能力的上限(也有可能降低 )
dropout
dropout有可能增加模型的容错能力,让模型变得健壮
损失函数
分类问题 交叉熵 连续问题 MSE
优化器
SGD :随机梯度下降 Adam :自适应,开始下降的快,当损失函数变小时,下降的步长变小,下降速度变慢
全连接
分类使用全连接
nn.Conv1d
参考