数学理论

 
线性指线性变换，y = w1*x1 + w2*x2 +...+wn*xn + b 
- xi是变量，n元一次变量，因变量,y因为它发生变化
- wi是权重 
- b是偏置，也叫截距

这是个万能公式，如果你的变量足够多，可以近似表示任何事物之间的关系

线性变换是n元一次方程，
变量y 与 x(x1,x2,...,xn,1) 的一个 线性组合(w1,w2,...,wn,b) 近似成 正比关系/线性关系
- 而不与某个变量成线性关系
- 

 
回归有几重含义：
1. 特指AI/统计学 中 连续/分类两大问题中的 连续问题，回归代表着连续，毕竟世界本质是连续的

2. 映射到本质，回到更底层，本源层面；
    用1维数据构建一个线性组合/结构，描述一个事物，
    反过来就是，将事物投影/映射到1维结构中，
    不管一个事物多么复杂，都可以通过构建一个1维线性结构近似描述
    复杂问题简单化，由高级/高维 回归 本质/低维

3. 空间有一个正交直角坐标系，每个维度都是线性的，
    将各个维度的数据排成一列，就得到一个维线性结构，
    这个结构可表示万物

4. 微分思想，任何高阶函数都可以通过微分化阶为一，用1维数据的积分表示

5. 量变达到质变，单个1维变量是简单的，三个臭皮匠却能抵上一个诸葛亮，当N多个变量出现时，可模拟万物
   - 单个人的力量弱
   - 团队的力量大，尤其是形成一定 组织/组合 之后力量更强

    

深度学习的线性回归

 
AI中使用向量表示一个样本x(x1,x2,...,xn)(行向量),w(w1,w2,...,wn)(列向量)
xw + b = y

深度学习的数据都是以批量形式存在的,一个批次X中有多个x
X@w + b = y
w与X每一行运算，然后映射到y，
等价于
批量数据X经过参数矩阵w转换，映射到向量y(y1,y2,...,yn)

每个样本x对应一个yi，所以X在前，W在后

相乘再相加

 
深度学习之中都是 相乘再相加 

在[0,1]的尺度上，相乘相加，以这种方式不断地 融合变换 

这有一种大道至简的感觉，不像机器学习那样，整合了高大上的理论或公式... 
- 如此简洁的方式，却可以 模拟/拟合 万物 
    

谁是变量，认是常量

 
x1,x2,...,xn 这组数形成一个向量，代表一个样本，是常量

w1,w2,...,wn 是权重，是算法自身要调整的值，这些值来自数据，是变量 

算法的学习就是要找到一组合适的wi，与样本向量线性组合，映射到 某个类别 
    

 
以上是训练过程，训练中需要学习参数

预测时，参数固定，参数与数据皆是常量
    

深度学习基本步骤

数据预处理：空值处理，归一化

模型定义:参数网络初始化， 计算方法 （不包含数据，数据只是流过参数网络）

损失函数设计：求极值,DL都是批次操作，实际是批次损失 极值的均值

模型参数优化方法设计：优化模型参数的方法 

 
训练：调用优化方法优化参数

预测：利用训练时相关参数处理数据，然后输入模型得到模型输出

模型保存与交付：数据预数据过程及参数，模型（模型参数，模型网络结构）

 
class Model(object):
    """
        机器学习模型骨架
    """
    def __init__(self, hyper_parameters):
        """
            定义超参数
        """
        self.hyper_parameters = hyper_parameters
    
    def fit(self, X, y):
        """
            训练过程
        """
        pass
    
    def predict(self, X):
        """
            定义预测过程
        """
        pass
  

 

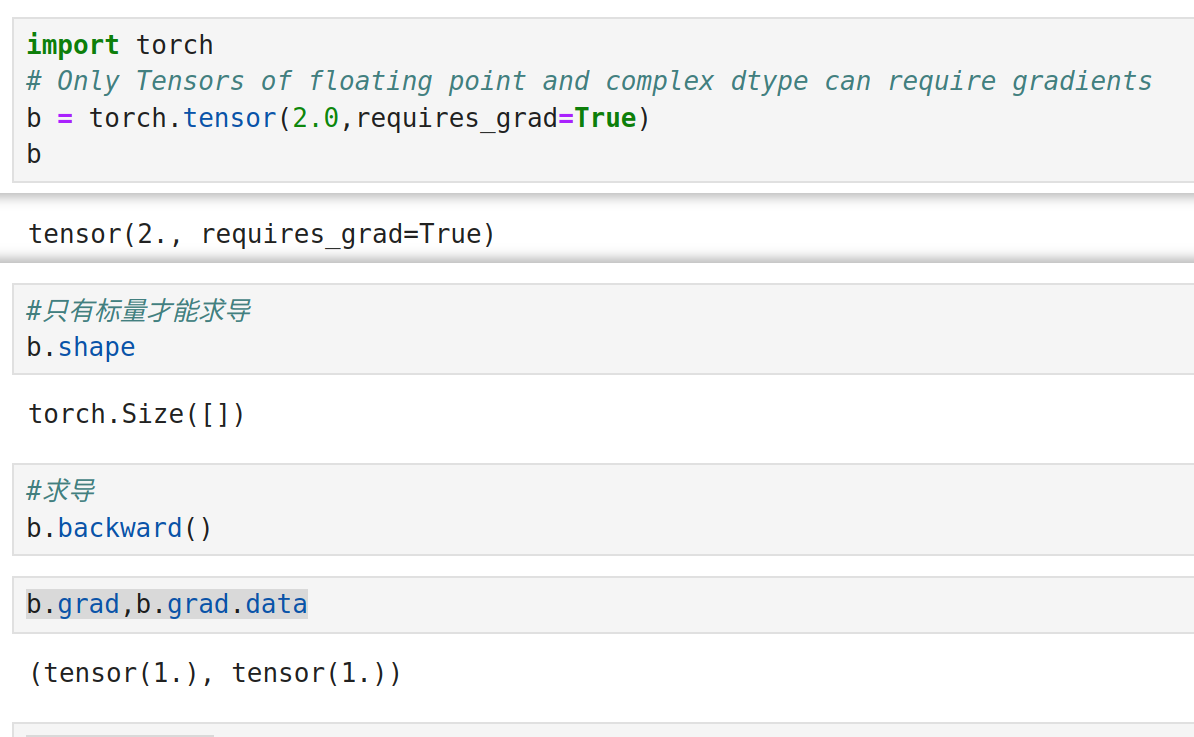
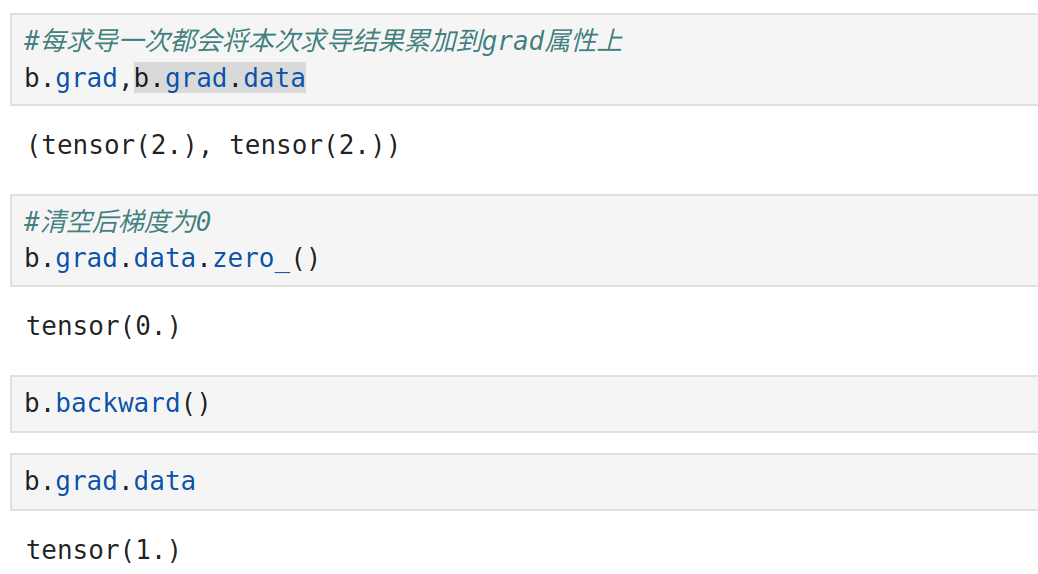
tensor设置为requires_grad=True后，将被看作一个变量  


zero_这种下划线写在单词末尾的方式，表示replace，
表示原地转换变量的值，而不是返回一个新变量
    

 
在 PyTorch 的自动微分系统中，
只有叶子张量（即那些直接由用户创建的张量，而不是通过其他张量计算得到的）的 
.grad 属性会被填充梯度信息。

如果一个张量是通过其他张量的操作得到的，那么它就不是叶子张量，其 .grad 属性默认不会被填充。
    

 
import torch 
w1 = torch.tensor(3.0,requires_grad=True)  
b = torch.tensor(2.0,requires_grad=True)  
y = w1*2 + b*1
y.backward()

if y.is_leaf:  #用户直接创建的
    print(y.grad)
else:
    print("y is not a leaf tensor")

    

 
此时的y是由其他张量计算得到的，y.grad不会被填充梯度

但要注意，深度学习也并不是要对y求偏导，y对应损失函数，

y.backward() 是梯度反向传播，最终求导的是参数变量  

w1.grad  # tensor(2.)
    

 
import torch 
w1 = torch.tensor([1.0,1.0],requires_grad=True)
b = torch.tensor(1.0,requires_grad=True)  
y = w1  + b # tensor([2., 2.], grad_fn=)
loss = y.sum() #转为标量
loss.backward()

 
w1.grad     # tensor([1., 1.])

b.grad      # tensor(2.)

 
w1有多个维度，每个维度都需要求一个偏导，皆被当作一个变量，
因为他们的系数永远一样，所以其梯度也一样

由于广播机制，变量b与w1的每个变量 进行了一次运算，相当于每个元素都有一个b，sum时相加了n次 

import torch

# tensor([0.1000, 0.2000], requires_grad=True)
w1 = torch.arange(0.1, 0.3, 0.1,requires_grad=True) 
w2 = torch.arange(0.01, 0.03, 0.01,requires_grad=True) 

# tensor([0.1000, 0.2000], requires_grad=True) tensor([0.0100, 0.0200], requires_grad=True)
print(w1,w2)

b = torch.tensor(0.1,requires_grad=True)  

y = w1*3 + w2*2 + b 
print(y.shape)        # torch.Size([2])
print(y.sum())        # tensor(1.1600, grad_fn=SumBackward0)
print(y.sum().shape)  # torch.Size([])

# torch只能对标量[]（单个数字的tensor）求导，y是shape为[3]的tensor
loss = y.sum()


# 对变量x求导，然后将求导结果赋值给tensor x的grad属性
# 每求一次导，就执行一次 x.grad = x.grad + grad
loss.backward()
print(w1.grad.data)    # tensor([3., 3.])
print(w2.grad.data)    # tensor([2., 2.])
"""
对每一个变量，即w1,w2分别求导
针对某个变量，有多个值，在每一个值处有一个导数
"""

print(b.grad.data)     # tensor(2.)
"""
常数的导数是0，但是b参数，是变量
所以b的导数是它的系数1
由于w1与b的shape并不一致，b向量只有一个数，在计算时会将b加到w1的每一个数上
即w1有多少个数，b就会被计算多少次，也就是广播机制
每一次计算，都会执行b.grad = b.grad + 1(b的导数)
w1有两个数，所以这里结果为2
"""

# 为防止累加，每计算完一次求导运算，就清空一次属性值 
w1.grad.data.zero_()
w2.grad.data.zero_()
b.grad.data.zero_()
print(w1.grad.data)    # tensor([0., 0.])
print(b.grad.data)

将参数的长度改为3,验证如下，结果与前面结论一致

import torch
w1 = torch.tensor(data=[0.1,0.2,0.3],requires_grad=True) 
w2 = torch.tensor(data=[0.01,0.02,0.03],requires_grad=True) 
b = torch.tensor(0.1,requires_grad=True)  
y = w1*3 + w2*2 + b 
loss = y.sum()
loss.backward()
print(b.grad.data)     # tensor(3.)

 

import numpy as np
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split
import torch
from sklearn.linear_model import LinearRegression
from sklearn.datasets import make_regression


# 随机生成的回归测试数据
X, y = make_regression(n_samples=2000, n_features=13)
X.shape,y.shape  #((2000, 13), (2000,))

X_train, X_test, y_train ,y_test = train_test_split(X, y, test_size=0.15, random_state=1)

# 特征归一化
mean_ = X_train.mean(axis=0)
std_ = X_train.std(axis=0)

# 处理训练数据
X_train = (X_train - mean_) / std_

# 处理测试数据
X_test = (X_test - mean_) / std_


lr1 = LinearRegression()
lr1.fit(X=X_train, y=y_train)

 

#参数w
lr1.coef_[:3]
array([95.26287774, 15.38262642, 74.11799156])

#偏置b
lr1.intercept_
-5.381843234898983

lr1.predict(X=X_test)[:3],y_test[:3]
(array([ -97.28120707,  -95.63686668, -147.64895265]),
 array([ -97.28120707,  -95.63686668, -147.64895265]))
    

 
机器学习中标签为向量,shape=(n,)
尝试学习中标签为矩阵，shape=(n,1)

y_test.shape  #(300,)
    

 
import numpy as np
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split
import torch
from sklearn.linear_model import LinearRegression
from sklearn.datasets import make_regression


# 随机生成的回归测试数据
X, y = make_regression(n_samples=2000, n_features=13)
X.shape,y.shape  #((2000, 13), (2000,))

X_train, X_test, y_train ,y_test = train_test_split(X, y, test_size=0.15, random_state=1)

"""
    数据转tensor
"""
# 检测是否有GPU
device = "cuda:0" if torch.cuda.is_available() else "cpu"
X_train1 = torch.tensor(data=X_train).to(dtype=torch.float64).to(device=device)
y_train1 = torch.tensor(data=y_train).to(dtype=torch.float64).to(device=device)
X_test1 = torch.tensor(data=X_test).to(dtype=torch.float64).to(device=device)
y_test1 = torch.tensor(data=y_test).to(dtype=torch.float64).to(device=device)
y_train1=y_train1.reshape(-1,1)
y_test1=y_test1.reshape(-1,1)
    

模型及参数，损失函数

 

def linear_regression(X, w, b):
    """线性回归(计算逻辑)
    """
    return X @ w + b

def loss_fn(y_pred, y_true):
    """mse损失函数
    """
    return ((y_pred - y_true) ** 2).mean()

#随机初始化模型的参数
w = torch.randn(13, 1, requires_grad=True, dtype=torch.float64, device=device)
b = torch.randn(1, requires_grad=True, dtype=torch.float64, device=device)
    

 
w.shape,b
(torch.Size([13, 1]),
 tensor([1.9541e-14], dtype=torch.float64, requires_grad=True))

模型参数不在于大小，随机初始化即可 

在于shape，要与数据X能进行矩阵运算 
参数要将一个样本向量的n个维度[n1,n2,...,nn]变换到一个维度上[类别]

    

 
def predict(X, w, b):
    with torch.no_grad():
        y_pred = linear_regression(X=X, w=w, b=b)
    return y_pred
    

训练

 

lr = 1e-2

for epoch in range(10000):
    
    # 正向传播 --- 模型输出，预测结果
    y_pred = linear_regression(X=X_train1, w=w, b=b)
    
    # 计算损失  --
    loss = loss_fn(y_pred=y_pred, y_true=y_train1)
    
    # 反向传播  -- 求w和b的偏导数
    loss.backward()
    
    # 更新参数
    w.data -= lr * w.grad
    b.data -= lr * b.grad
    
    # 清空梯度
    w.grad.data.zero_()
    b.grad.data.zero_()
    
    # 过程监控
    if epoch % 1000 == 0:
        print(loss.item())
    

 
32887.253607779305
9.500932702751085e-13
5.664800872938198e-25
5.666899667315686e-25
5.666979629969325e-25
5.66737335508748e-25
5.6672913877990685e-25
5.6672913877990685e-25
5.666897662680915e-25
5.666897662680915e-25
    

 
predict(X=X_test1, w=w, b=b)[:3]
tensor([[ 209.9008],
        [ -86.7581],
        [-154.0384]], dtype=torch.float64)


y_test1[:3]
tensor([[ 209.9008],
        [ -86.7581],
        [-154.0384]], dtype=torch.float64)

 
w[:3]
tensor([[1.2952e+01],
        [2.0628e-14],
        [1.1275e+01]], dtype=torch.float64, grad_fn=)

b
tensor([1.9541e-14], dtype=torch.float64, requires_grad=True)

    

import torch
from ai.datasets import load_boston

# -------------------------------------------------
# 数据预处理
# -------------------------------------------------

def get_data():
    X_train,y_train, X_test, y_test = load_boston()

    # 从训练集中提取参数
    mean_ = X_train.mean(axis=0)   # 按列方向取均值,
    std_ = X_train.std(axis=0)     # 相同特征的一列数据归一

    # 预处理训练集和测试集
    X_train1 = (X_train - mean_) / std_
    X_test1 = (X_test - mean_) / std_ 

    # 共享内存
    X_train = torch.from_numpy(X_train1).float()
    X_test = torch.from_numpy(X_test1).to(dtype=torch.float32)

    # 标签转列向量
    y_train = torch.from_numpy(y_train.reshape((-1, 1))).float()
    y_test = torch.from_numpy(y_test.reshape((-1, 1))).float()

    return X_train,y_train, X_test, y_test


# -------------------------------------------------
# 模型构造
# -------------------------------------------------
class LinearRegression(object):
    """模型构造:线性回归
    """
    loss = None

    def __init__(self, device=None) -> None:
        if device:
            self.device = device
        else:
            # 若存在GPU则使用GPU
            self.device = "cuda:0" if torch.cuda.is_available() else "cpu"

        # 定义模型的参数
        self.w = torch.randn(13, 1, requires_grad=True, dtype=torch.float32, device=device)
        self.b = torch.randn(1, requires_grad=True, dtype=torch.float32, device=device)
        # print(b)   # tensor([0.1403], requires_grad=True)
        # stp(b,"b")   # shape:torch.Size([1]), type:class 'torch.Tensor', b

    def forward(self, X):
        return X@self.w + self.b

    # -------------------------------------------------
    # 损失函数设计
    # -------------------------------------------------
    @classmethod
    def loss_fn(cls, y_pred, y_true):
        cls.loss = ((y_pred - y_true) ** 2).mean()
        return cls.loss

    def grad_reduce(self, learning_rate):
        """梯度下降法
        一种优化方法，让模型输出不断接近真实标签的方法
        梯度指导数
        """
        # 使用导数优化更新参数
        self.w.data -= learning_rate * self.w.grad.data
        self.b.data -= learning_rate * self.b.grad.data 

        # 清空梯度，以防止不断累加
        self.w.grad.data.zero_()
        self.b.grad.data.zero_()

    def print_loss(self):
        print(self.loss.item())

    
    def train(self, X,y, learning_rate, loss_fn=None):
        """训练
        每训练一次，就优化一次参数
        """

            # 正向传播
        y_pred = self.forward(X=X)

        # print("y pred",y_pred[1],"y label",y_train[1])
        
        # 模型预测与真实标签间的差异
        if loss_fn:
            loss = loss_fn(y_pred, y)
        else:
            loss = self.loss_fn(y_pred=y_pred, y_true=y_train)
        
        # 反向传播，逆向求偏导grad
        loss.backward()
        model.grad_reduce(learning_rate=learning_rate)


    def predict(self, X):
        """
            模型预测
        """
        with torch.no_grad():
            y_pred = self.forward(X=X)
        return y_pred 


def batch_train(model, X, y, learning_rate=1e-2, epochs=300):
    """训练
    梯度下降法求函数极值
    """
    for epoch in range(epochs):
        model.train(X=X,y=y, learning_rate=learning_rate)
        
        # 过程监控
        model.print_loss()

if __name__=="__main__":
    X_train,y_train, X_test, y_test = get_data()

    # from ai.box.base import stp 
    # stp(y_test,"y_test")  # shape:torch.Size([76, 1]), type:class 'torch.Tensor', y_test
    # print(y_test.dtype)   # torch.float32

    # 若存在GPU则使用GPU
    device = "cuda:0" if torch.cuda.is_available() else "cpu"
    X_train.to(device=device)
    y_train.to(device=device) 
    X_test.to(device=device) 
    y_test.to(device=device)

    model = LinearRegression()
    batch_train(model=model,X=X_train,y=y_train)
    """
    587.739013671875
    545.857666015625
    510.1678161621094
    ......
    23.185871124267578
    23.183822631835938
    23.181793212890625
    """

    y_pred = model.predict(X=X_test)
    print(y_pred)
    """
    tensor([[17.6774],
            [25.3967],
            [36.5577],
    ...
    ...
    ...
            [28.7579],
            [29.5272],
            [32.7000]])
    """

重点分析：

1. 模型定义：X@self.w + self.b 
2. 损失函数设计： MSE，((y_pred - y_true) ** 2).mean() 

 
import numpy as np
import torch 
from torch import nn 
import torch.nn.functional as F 

# torch 批次处理
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split

# 因为加入了1%的噪声，所以，不管怎么训练，模型的精度上限是 99%，会有稍许浮动，但不会达到100%
# 这也说明影响精度的两个重要因素：一是模型算法不够好，二是数据噪声太多(这个决定了上限)
X,y = make_regression(n_samples=10000,n_features=100,noise=0.01,random_state=73)
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.1,random_state=73)

class MyDataSet(Dataset):
    
    def __init__(self,X,y):
        """
        构建数据集
        """
        self.X = X
        self.y = y.reshape(-1,1)
        print(f"seq_len={len(X[0])}")
    
    def __len__(self):
        return len(self.X)
    
    def __getitem__(self, idx):
        x = self.X[idx]
        y = self.y[idx]

        return torch.tensor(data=x).float(), torch.tensor(data=y).float()

# 自定义数据加载器
train_dataset = MyDataSet(X=X_train,y=y_train)
test_dataset = MyDataSet(X=X_test,y=y_test)


# -----------------------------
# 模型定义
# -----------------------------
class LinearModel(nn.Module):
    def __init__(self, in_features=100, out_features=1):
        """初始化网络参数"""
        super().__init__()
        self.linear = nn.Linear(in_features=in_features, out_features=out_features)

    def forward(self, X):
        """让数据流过参数网络"""
        x = self.linear(X) 
        return x

#模型
model = LinearModel(in_features=100, out_features=1)

#损失函数
loss_fn = nn.MSELoss()

#优化器 
optim = torch.optim.Adam(params=model.parameters(),lr=1e-3)

# 从数据集中批次取数据
train_dataloader = DataLoader(dataset=train_dataset, shuffle=True, batch_size = 128)

# 训练一行数据,测试代码是否有误
for X,y in train_dataloader:
    print(X.shape,X.ndim,y.shape,y.ndim)  # torch.Size([128, 100]) 2 torch.Size([128, 1]) 2
    y_out = model(X)
    if y_out.ndim != y.ndim:
        print('模型输出数据维度与标签维度不一致，无法进行损失计算...')
        print('y_out:',y_out.shape,y_out.ndim)  # torch.Size([128, 1]) 2
        break
    loss = loss_fn(y_out,y)
    optim.zero_grad()
    loss.backward()
    optim.step()
    break 
# ------------------
# 重要：参数网络定义（模型定义），如何让参数逼近标签（损失函数设计及优化方法）
# ------------------
    
    

数据集

 
from tpf.dl import MyDataSet
from tpf.dl import log
from tpf.dl import DMEval


import numpy as np
import torch 
from torch import nn
# torch 批次处理
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split

# 因为加入了1%的噪声，所以，不管怎么训练，模型的精度上限是 99%，会有稍许浮动，但不会达到100%
# 这也说明影响精度的两个重要因素：一是模型算法不够好，二是数据噪声太多(这个决定了上限)
X,y = make_regression(n_samples=10000,n_features=100,noise=0.01,random_state=73)
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.1,random_state=73)

device = "cuda:0" if torch.cuda.is_available() else "cpu"

# 自定义数据加载器
train_dataset = MyDataSet(X=X_train,y=y_train)
test_dataset = MyDataSet(X=X_test,y=y_test)

模型，损失函数，优化器

 
# -----------------------------
# 模型定义
# -----------------------------
from tpf.dl import LinearModel

#模型
model = LinearModel(in_features=100, out_features=1)

#损失函数
loss_fn = nn.MSELoss()

#优化器 
optim = torch.optim.Adam(params=model.parameters(),lr=1e-3)

# 从数据集中批次取数据
# train_dataloader = DataLoader(dataset=train_dataset, shuffle=True, batch_size = 128)

训练

 
from tpf.dl import T
T.train(model=model, 
            loss_fn=loss_fn,
            optimizer="adam", 
            train_dataset=train_dataset, test_dataset=test_dataset,
            epochs=3, 
            batch_size=128,
            learning_rate=1e-3,
            model_param_path="ml_model1_params.h5",
            auto_save=True,
            continuation=True,  #是否在之前训练的基础上进行训练
            is_regression=True,
            log_file="/tmp/train.log")