线性回归概述
任务分析
问题分类:回归是连续问题,这里房价数据集,MSE作为损失函数 数据处理: 训练集,测试集拆分; 归一化; 转dataset 模型定义:一层全连接 学习训练: 损失函数MSE,优化器:SGD ; 输入训练集,循环训练; 中间输出损失函数大小,精度等以便观察 预测处理: 使用测试集进行预测, 模型的输出就是房价,不需要额外处理
怎么看数据集
房价数据集
from ai.datasets import load_boston # 加载数据 X_train, y_train, X_test, y_test = load_boston() shape:(430, 13), type:class 'numpy.ndarray', X_train shape:(430,), type:class 'numpy.ndarray', y_train
以向量,向量组的角度看数据集
学术界默认所有向量为列向量 训练集是一个shape为(430,13)的矩阵 从数据集的角度看,整个数据集有13个向量,每个向量430维, 每个维数430的向量都是房价一个维度的数据,可计算 均值,标准差 向量维数430,向量组个数为13, 数据处理的时候,要从这个角度看数据集
一个样本表示的向量
通常使用小写的x表示一个样本向量,如果按数学理论,它是一个列向量 这里13个维度表示一个样本,在数学理论上差不多是这个样子 [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 ] 在落地计算的时候,列向量与行向量无任何区别, 实际上常用的样本是按行写的,它是下面这个样本 x=[1,2,3,4,5,6,7,8,9,10,11,12,13] 这二者容易混淆,区分方法有二: 1. 看场景,如果你是在看书,请把所有向量默认按列向量看 2. 如果你在敲击键盘,请把数据集的一个样本看成行向量 下面是全连接的计算公式
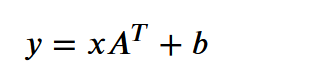
x就是一个样本,这里的x是行向量, [1,13]@[13,1]= [1] 把一个13维的向量变换成1维,因为这里是回归问题 不要太在意公式怎么写,关键是shape对的上就可以了 全连接公式写经常写成 xw + b = y 意为把x变换到y,y与标签同维
数据处理
标签shape处理
# 标签shape处理,一个标签为一个向量 y_train = y_train.reshape((-1, 1)) y_test = y_test.reshape((-1, 1)) y_test.shape (76, 1) 模型输出,标签 会作为损失函数的参数,通常情况下它们同shape 连续问题,模型使用全连接, 输入数据的维度是13, 输出为1维,本意是输出一个数就是行, 但深度学习中的维度转换,也就是线性变换,数据全是有维度的,至少1维 在pytorch中,单个数字没有维度或维度为0,1维就是1维数组/列表 模型从13维转换到1维,其一个样本对应的结果就是[1]这样的格式 后面会展示模型的输出 所以,这里将标签的维度从0提升到1 这一步,要求心中对 模型维度转换,损失函数参数,标签维度 三者shape了然于胸, 是整体打通流程后,第二遍回来看时,才能做到的, 第一遍知道有这个事就行了
均值
取均值处理,以测试集为例,数据有76行,13列, X_test.shape (76, 13) 归一化,是要对一列做处理,是要取一列的均值, 即要对76这个数字所在的维度,就是dim=0这一维度取均值 就2维矩阵,dim=0表示列方向, 因此均值为 X_test.mean(axis=0,keepdims=False).shape (13,) 有13列,每列一个均值,有13个均值 xx_: 单个末尾下划线(后缀)是一个约定,用来避免与Python关键字产生命名冲突;
标准化公式
(数据 - 均值)/ 标准差 这里数据的shape为(76,13),是二维 均值的shape为(13,),是一维 一个二维矩阵 减 一维矩阵,首先会对一维矩阵升维,升到与二维同shape, 也就是说,会将(13,)变成(76,13) 会将(13,)这样的向量,复制76份, 数据[76,13] - 均值(13,) = 数据[76,13] - 均值(76,13) = 新数据[76,13] 后面是除法,这个是重点,除法并不在指定的向量线性运算中, 走的更不是矩阵运算,即不是向量内积 走的是,向量位乘,按位运算 同样先将标准差的维度从(13,)升到(76,13) 然后按位操作,相同位置上的前后两个矩阵上的元素,分别相除 运算后的矩阵shape不变
标准化的目的
(数据-均值)/标准差 标准差就是方差的开平方, 是一个数据分布内部离散量的累加再求平均, 可 近似看作 整体数据离“数据中心点”的距离的平均值 这么一系列操作后,得到的是啥? 将数据转化为均值为0,标准差为1 的正态分布,即标准正态分布 为什么要这么做?为什么呢? 因为数据处理时,处理的多个数据分布,要对比就得有个统一的量纲, 处理方法就是,不管你原来是什么分布,数据的均值多少,离散程度怎么样, 我统一给你转成均值为1方差为1的标准正态分布 这是能够多列一起处理的 基石/起点/前提 注意: 让均值为0,标准差为1,就是所有数据离中心点平均距离为1, 并不意味着各个数据分布会变得一模一样 他们的形态仍然是千差万别 比如,在一个平面坐标系上,给你两个数,可正可负, 只要求,他们的均值为0,到原点距离为1, 以原点为圆心,取直径与圆相交的两个点,为一对数据, 那么,符合要求的数据可以取无数对, 他们都符合,均值为0,到均值0的平均距离为1, 这才是两个数据点中一种特殊的数据分布... 所以,让数据分布的均值为0,标准差为1, 并没有让所有数据分布变得一模一样, 只是统一了量纲,有了比较/计算的前提
数据预处理
# 数据预处理 mean_ = X_train.mean(axis=0) std_ = X_train.std(axis=0) X_train = (X_train - mean_) / std_ X_test = (X_test - mean_) / std_ 四行代码,但你的脑海中要闪现出以下内容: 每列都是一个分布 求分布均值 求分布标准差 将每列化为正态分布, 这里使用是z-score,归一化中的标准化, 将分布转化为一个均值为0,标准差为1的正态分布, 即标准正态分布 矩阵shape的变换 有向量线性运算, 也有向量位乘 但真的没有矩阵乘法运算,即没有向量内积
批次加载
import torch
from torch import nn
# 数据打包
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
class MyDataset(Dataset):
"""自定义数据集
"""
def __init__(self, X, y):
"""超参
"""
self.X = X
self.y = y
def __getitem__(self, idx):
"""根据索引返回一对数据 (x, y)
"""
return torch.tensor(data=self.X[idx]).float(), torch.tensor(data=self.y[idx]).float()
def __len__(self):
"""数据总数
"""
return len(self.X)
# 训练集加载器
train_dataset = MyDataset(X=X_train, y=y_train)
train_dataloader = DataLoader(dataset=train_dataset, batch_size=32, shuffle=True)
train_dataset[0]
(tensor([-0.3971, -0.4946, -0.3633, -0.2689, -0.2868, -0.6296, 0.8480, -0.7475,
-0.5148, -0.1354, 1.1539, 0.4311, 0.8525]),
tensor([19.5000]))
len(train_dataset)
430
for x,y in train_dataloader:
print(x.shape,y.shape)
break
torch.Size([32, 13]) torch.Size([32, 1])
# 测试集加载器,不需要shuffle
test_dataset = MyDataset(X=X_test, y=y_test)
test_dataloader = DataLoader(dataset=test_dataset, batch_size=32, shuffle=False)
模型定义
从数据到标签的shape变换
torch.Size([32, 13]) torch.Size([32, 1]) 数据:32一个批次,每个样本13维 标签:32一个批次,每个样本1维 特征变换:将13变为1,这就是模型要做的
nn.Linear()
nn.Linear(
in_features: int,
out_features: int,
bias: bool = True,
device=None,
dtype=None,
) -> None
y = xA^T + b
import torch
from torch import nn
X = torch.randn(32,13)
# 先定义一个类模板,并生成一个模板对象,这个过程会初始化一组参数矩阵A与b
line_layer = nn.Linear(in_features=13,out_features=1)
# 调用该对象
y_out = line_layer(X)
y_out.shape
torch.Size([32, 1])
for param in line_layer.parameters():
print(param)
Parameter containing:
tensor([[-0.2485, 0.0003, -0.2262, -0.2724, -0.2261, -0.2296, 0.0148, -0.1113,
0.0652, 0.1598, 0.2040, -0.0722, -0.1204]], requires_grad=True)
Parameter containing:
tensor([-0.1196], requires_grad=True)
模型定义
class LinearRegression(nn.Module):
"""模型定义
"""
def __init__(self, in_features, out_features):
"""参数网络设计
- 总体来说,做的事件是将数据从一个维度转换到另外一个维度
"""
super().__init__()
self.linear = nn.Linear(in_features=in_features, out_features=out_features)
def forward(self, X):
"""正向传播
- 调用定义的参数网络
- 让数据流过参数网络,常量数据流过不过的参数产生不同的值
- 这个过程参数本身不会变
- 让参数变化的是后面的优化器
"""
out = self.linear(X)
return out
model = LinearRegression(in_features=13, out_features=1)
model
LinearRegression(
(linear): Linear(in_features=13, out_features=1, bias=True)
)
该自定义模型中只有一个线性模型Linear
其参数也只有线性模型的参数,
在init方法中完成Linear模板类的初始化,也就完成了参数的初始化
for param in model.parameters():
print(param)
Parameter containing:
tensor([[-0.2292, -0.1510, 0.2504, 0.0500, -0.2287, 0.1542, -0.1364, -0.1282,
-0.2764, -0.0922, 0.1389, 0.0320, 0.0816]], requires_grad=True)
Parameter containing:
tensor([-0.0371], requires_grad=True)
forward方法
输入为批次数据,调用参数网络进行计算,然后输出结果
模型验证
X = torch.randn(30,13) y_out = model(X) y_out.shape torch.Size([30, 1]) 使用随机数验证一下模型是否与预期相符, 数据分批后,最后一批未必刚好就是32,大概率不是
训练-损失函数
损失函数
# 损失函数 loss_fn = nn.MSELoss()
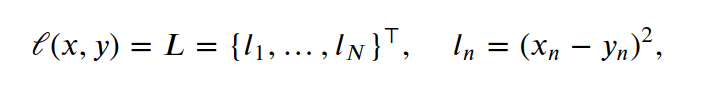
where :math:`N` is the batch size. If :attr:`reduction` is not ``'none'``(default ``'mean'``), then:
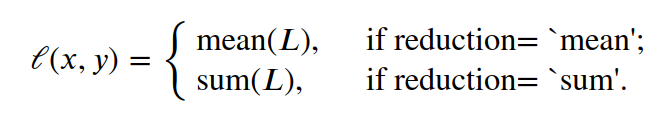
MSE损失计算
每个样本与标签之间都有个损失,一个批次有n个损失, 默认求均值,因此批次损失的结果是一个标量, 另外,损失函数的结果是一个批次的均值, 在pytorch中,任何数都是一个tensor,这个均值也是如此, tensor对象上还附加有一系列方法,比如反向传播 X = torch.randn(30,13) y_out = model(X) y = torch.randn(30,1) # 损失函数 loss_fn = nn.MSELoss() loss = loss_fn(y_out, y) loss tensor(1.4462, grad_fn=MseLossBackward0)
损失函数反向传播
loss.backward()
损失函数以 模型输出和标签 为参数,这才是整个工程中的总函数
loss_fn = nn.MSELoss()
损失函数中的常量与变量各是什么?
常量就是数据,输入的数据自来业务,是不会变的
变量就是参数,参数才是变量,类似下面的公式
y = 3w + b
3在前,w在后,写成数据的样本,就是
y_out = xw + b
数学公式通常将常量写在变量的前面,
书上经常是这么写的y=3x+1,导致我们潜意识中总是认为x是变量
其实谁是变量主要看业务逻辑,x本身就是一个字母符号,
在AI中,x代表的是数据中的一个样本,是常量,w才是那个变量
反向传播,是一种逆向求导的过程,就简单看作求导吧
y = 3w + b 若对w求偏导,那么函数y的导数恒为3,
MSE计算的是差的平方,包括了平方计算,
那么它的导函数就是一个关于w的一次函数
pytorch在损失函数反向传播,也就是求导时,
将变量w在x处的梯度存入w.grad.data中,
并且是累加
for param in model.parameters():
print(param.grad.data)
tensor([[ 0.0172, -1.7931, 1.6512, 0.3874, 0.2149, -0.3993, -1.0178, -1.1852,
-2.4712, -0.1330, 1.1420, -1.2974, -0.1388]])
tensor([1.0219])
到这里变参本身本身尚无变化,只是所在对象tensor.gard.data被放了历史累计的梯度
for param in model.parameters():
print(param)
Parameter containing:
tensor([[-0.2292, -0.1510, 0.2504, 0.0500, -0.2287, 0.1542, -0.1364, -0.1282,
-0.2764, -0.0922, 0.1389, 0.0320, 0.0816]], requires_grad=True)
Parameter containing:
tensor([-0.0371], requires_grad=True)
训练-批次
重全局而弱个体
损失函数的公式中,损失的计算是批次的均值 实际上每个样本与标签都有一个损失,有的损失大有的损失小 一个批次中那个损失小的参数是否值得保留? 不着急回答这个问题,先来看看概率: 概率不同的频率,频率是统计结果,一个频率是与一个样本绑定的, 而概率具有普遍意义,比如抛一次硬币出现正面的概率是二分之一, 这种先验概率可以代入数学公式进行推理,而频率达不到这种程度 但 ... 虽说抛一次硬币出现正面的概率是二分之一,你抛两次就敢说一定出正面吗? 不敢 飞行员跳伞用的那个伞,最初时,人跳下去伞打不开的概率是百分之一,你敢用吗? 不敢 概率,对个体而言它很不准,只有数据量达到一定规模时,才具有“统计”意义 即使损失函数计算的不是概率,但仍在统计学的范畴,仍有数理统计的规律在其中, 所以,统计损失时,不是按个体进行统计,而是批次, 这也意味着,批次通常不要太小, 要能一定程度上 代表/反映 全体数据集的性质才行 另外,计算机中为什么要用批次?批次在落地计算时的意义何在? 那是因为,如果代入全体数据集,计算机可能计算不动, 无奈才小批次计算... 如果条件允许,批次要尽量大一些
训练-优化器
模型参数更新:优化器
训练的目的:期望得到一组符合要求的参数 这个工作由优化器来处理 原理:梯度下降法 w = w - 学习率*w.grad.data 学习率是一个小于1的数, 目的在于控制每次参数的改变量, 防止它一次变化太大,导致跨过最优解 w.grad.data,就是梯度,导数, 也就是梯度下降法,最核心的点在哪里? 在于它有正负 如果只有一个变量,随便给个足够小的数,一点点改变,也能找到最优解 但现在问题是变量有N多个,每个变量的正负变化方向不一样, 而梯度,也就是导数, 小于0表示下降,大于0表示在上升,能准确在表示每个变参的增减 它可以让每个变参都向着各自维度上最低点走去, 当所有变参都走到自己的最低点附近时,就是整个损失函数的最低点 # 优化器 optimizer = torch.optim.SGD(params=lr.parameters(), lr=1e-2) SGD是随机梯度下降,常用的还有自适应torch.optim.Adam, torch.optim包下还有很多其他优化器,可自行研究
# 优化一次
optimizer.step()
# 然后模型参数就会变化一次
for param in model.parameters():
print(param)
Parameter containing:
tensor([[-0.2248, -0.1468, 0.2516, 0.0496, -0.2243, 0.1527, -0.1342, -0.1232,
-0.2775, -0.0989, 0.1355, 0.0304, 0.0789]], requires_grad=True)
Parameter containing:
tensor([-0.0366], requires_grad=True)
训练-数据可重复使用
数据被使用一次,参数就被更新一次 但一次更新,未必会达到损失函数梯度的最低点的附近,可能还有很远的距离 如此,数据就可以循环/重复使用
一轮训练
# 模型对象
model = LinearRegression(in_features=13, out_features=1)
# 损失函数
loss_fn = nn.MSELoss()
# 优化器
optim = torch.optim.SGD(params=model.parameters(), lr=1e-2)
# 一轮训练
for X,y in train_dataloader:
y_out = model(X)
loss = loss_fn(y_out, y)
# 求当前参数在当前数据处的梯度
loss.backward()
print(loss.item())
# 下降一次,就是朝着最优解的方向前进一步
optim.step()
optim.zero_grad()
563.1500854492188
529.769287109375
552.975830078125
569.2049560546875
466.73284912109375
469.0701599121094
452.25543212890625
445.3332824707031
385.3167419433594
512.1915893554688
481.2800598144531
455.5694274902344
265.6980895996094
331.1587219238281
多轮训练
def trans(epoch,
batch_size=32,
dataset=train_dataset,
model=model,
loss_fn=loss_fn,
optim=optim):
"""多轮训练
"""
train_dataloader = DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
for i in range(1,epoch+1):
print(f"...第{i}轮训练开始....\n")
# 一轮训练
for X,y in train_dataloader:
y_out = model(X)
loss = loss_fn(y_out, y)
# 求当前参数在当前数据处的梯度
loss.backward()
print(loss.item())
# 下降一次,就是朝着最优解的方向前进一步
optim.step()
optim.zero_grad()
print("-------------------------\n")
trans(epoch=2)
...第1轮训练开始....
599.859130859375
689.5206298828125
517.9083251953125
453.3288269042969
506.0191650390625
585.3128662109375
398.93548583984375
541.7645874023438
385.9604797363281
442.7764892578125
336.8048095703125
380.02935791015625
464.0787353515625
381.2884216308594
-------------------------
...第2轮训练开始....
281.2172546386719
411.74871826171875
367.2362365722656
283.3430480957031
376.3662109375
297.74468994140625
197.08645629882812
222.76084899902344
338.5317077636719
229.46780395507812
197.31729125976562
235.1333770751953
195.02389526367188
184.9523162841797
-------------------------
训练-过程监控
损失监控
import numpy as np
test_dataset = MyDataset(X=X_test, y=y_test)
def get_loss(dataset, model=model, loss_fn=loss_fn, batch_size=128):
"""以整个数据集为基的损失评估
"""
dataloader = DataLoader(dataset=dataset, batch_size=batch_size, shuffle=False)
with torch.no_grad():
batch_loss = []
for X, y in dataloader:
y_out = model(X)
loss = loss_fn(y_out, y)
batch_loss.append(loss.item())
mean_loss = np.array(batch_loss).mean()
return mean_loss.round(4)
def trans(epoch,
batch_size=32,
train_dataset=train_dataset,
test_dataset=test_dataset,
model=model,
loss_fn=loss_fn,
optim=optim):
"""多轮训练
"""
train_dataloader = DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
for i in range(1,epoch+1):
print(f"...第{i}轮训练开始....\n")
# 一轮训练
count = 0
for X,y in train_dataloader:
count = count+1
y_out = model(X)
loss = loss_fn(y_out, y)
# 求当前参数在当前数据处的梯度
loss.backward()
if count%7==6:
print(round(loss.item(),4))
# 下降一次,就是朝着最优解的方向前进一步
optim.step()
optim.zero_grad()
epoch_loss_train = get_loss(dataset=train_dataset, model=model, loss_fn=loss_fn)
epoch_loss_test = get_loss(dataset=test_dataset, model=model, loss_fn=loss_fn)
print(f"第{i}轮训练,模型输出与训练集偏差:{epoch_loss_train},与测试集偏差:{epoch_loss_test}")
print("-------------------------\n")
trans(epoch=2)
...第1轮训练开始....
497.1451
385.3959
第1轮训练,模型输出与训练集偏差:362.3831,与测试集偏差:260.6301
-------------------------
...第2轮训练开始....
362.2549
215.1881
第2轮训练,模型输出与训练集偏差:217.4191,与测试集偏差:145.0836
-------------------------
精度监控
预测处理
多跑几个批次
trans(epoch=20) ...第7轮训练开始.... 35.5381 21.4963 第7轮训练,模型输出与训练集偏差:37.6273,与测试集偏差:18.4797 ------------------------- ...第8轮训练开始.... 29.2791 29.9498 第8轮训练,模型输出与训练集偏差:32.6934,与测试集偏差:16.8172 ------------------------- ...第9轮训练开始.... 25.7375 45.8575 第9轮训练,模型输出与训练集偏差:29.5915,与测试集偏差:16.5234 ------------------------- ...第10轮训练开始.... 47.0189 21.1816 第10轮训练,模型输出与训练集偏差:27.9589,与测试集偏差:16.5747 ------------------------- ...第11轮训练开始.... 22.6338 36.2648 第11轮训练,模型输出与训练集偏差:26.9055,与测试集偏差:16.8762 ------------------------- ...第12轮训练开始.... 19.1486 31.5116 第12轮训练,模型输出与训练集偏差:26.2493,与测试集偏差:17.2252 ------------------------- ...第13轮训练开始.... 11.7521 21.8944 第13轮训练,模型输出与训练集偏差:25.7086,与测试集偏差:17.5082 ------------------------- ...第14轮训练开始.... 12.7284 21.849 第14轮训练,模型输出与训练集偏差:25.4166,与测试集偏差:17.7007 ------------------------- ...第15轮训练开始.... 10.8912 29.8508 第15轮训练,模型输出与训练集偏差:25.226,与测试集偏差:17.7393 ------------------------- ...第16轮训练开始.... 21.1807 22.1289 第16轮训练,模型输出与训练集偏差:25.0299,与测试集偏差:18.0463 ------------------------- 从第11轮开始,损失开始慢慢变大了...
调用模型输出即预测
def predict(X,model):
"""预测
"""
with torch.no_grad():
y_out = model(X)
return y_out
test_dataloader = DataLoader(dataset=test_dataset, batch_size=128, shuffle=False)
for X, y in test_dataloader:
y_pred = predict(X=X, model=model)
print(y_pred[:5],y[:5])
print(((y_pred - y) ** 2).mean())
break
tensor([[17.5243],
[24.8794],
[36.0807],
[18.9943],
[20.5612]]) tensor([[17.4000],
[23.9000],
[36.0000],
[12.1000],
[19.6000]])
tensor(18.5860)
训练模型传参是引用
def trans(epoch,
batch_size=32,
train_dataset=train_dataset,
test_dataset=test_dataset,
model=model,
loss_fn=loss_fn,
optim=optim):
model对象传入trans方法,是以引用的方式传入的
在trans方法修改了model对象的参数
trans方法结束后,model对象的参数永久地发生了变化
故后续可直接使用model对象进行预测
线性回归全代码
from ai.datasets import load_boston
# 加载数据
X_train, y_train, X_test, y_test = load_boston()
# 标签shape处理,一个标签为一个向量
y_train = y_train.reshape((-1, 1))
y_test = y_test.reshape((-1, 1))
# 数据预处理
mean_ = X_train.mean(axis=0)
std_ = X_train.std(axis=0)
X_train = (X_train - mean_) / std_
X_test = (X_test - mean_) / std_
import torch
from torch import nn
# 数据打包
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
class MyDataset(Dataset):
"""自定义数据集
"""
def __init__(self, X, y):
"""超参
"""
self.X = X
self.y = y
def __getitem__(self, idx):
"""根据索引返回一对数据 (x, y)
"""
return torch.tensor(data=self.X[idx]).float(), torch.tensor(data=self.y[idx]).float()
def __len__(self):
"""数据总数
"""
return len(self.X)
# 训练集加载器
train_dataset = MyDataset(X=X_train, y=y_train)
# train_dataloader = DataLoader(dataset=train_dataset, batch_size=32, shuffle=True)
class LinearRegression(nn.Module):
"""模型定义
"""
def __init__(self, in_features, out_features):
"""参数网络设计
- 总体来说,做的事件是将数据从一个维度转换到另外一个维度
"""
super().__init__()
self.linear = nn.Linear(in_features=in_features, out_features=out_features)
def forward(self, X):
"""正向传播
- 调用定义的参数网络
- 让数据流过参数网络,常量数据流过不过的参数产生不同的值
- 这个过程参数本身不会变
- 让参数变化的是后面的优化器
"""
out = self.linear(X)
return out
# 模型对象
model = LinearRegression(in_features=13, out_features=1)
# 损失函数
loss_fn = nn.MSELoss()
# 优化器
optim = torch.optim.SGD(params=model.parameters(), lr=1e-2)
import numpy as np
test_dataset = MyDataset(X=X_test, y=y_test)
def get_loss(dataset, model=model, loss_fn=loss_fn, batch_size=128):
"""以整个数据集为基的损失评估
"""
dataloader = DataLoader(dataset=dataset, batch_size=batch_size, shuffle=False)
with torch.no_grad():
batch_loss = []
for X, y in dataloader:
y_out = model(X)
loss = loss_fn(y_out, y)
batch_loss.append(loss.item())
mean_loss = np.array(batch_loss).mean()
return mean_loss.round(4)
def trans(epoch,
batch_size=32,
train_dataset=train_dataset,
test_dataset=test_dataset,
model=model,
loss_fn=loss_fn,
optim=optim):
"""多轮训练
"""
train_dataloader = DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
for i in range(1,epoch+1):
print(f"...第{i}轮训练开始....\n")
# 一轮训练
count = 0
for X,y in train_dataloader:
count = count+1
y_out = model(X)
loss = loss_fn(y_out, y)
# 求当前参数在当前数据处的梯度
loss.backward()
if count%7==6:
print(round(loss.item(),4))
# 下降一次,就是朝着最优解的方向前进一步
optim.step()
optim.zero_grad()
epoch_loss_train = get_loss(dataset=train_dataset, model=model, loss_fn=loss_fn)
epoch_loss_test = get_loss(dataset=test_dataset, model=model, loss_fn=loss_fn)
print(f"第{i}轮训练,模型输出与训练集偏差:{epoch_loss_train},与测试集偏差:{epoch_loss_test}")
print("-------------------------\n")
trans(epoch=20)
def predict(X,model):
"""预测
"""
with torch.no_grad():
y_out = model(X)
return y_out
test_dataloader = DataLoader(dataset=test_dataset, batch_size=128, shuffle=False)
for X, y in test_dataloader:
y_pred = predict(X=X, model=model)
print(y_pred[:5],y[:5])
print(((y_pred - y) ** 2).mean())
break
矩阵相乘+nn.Parameter
|
模型改变,nn.Parameter加载参数,其他不变
import torch
from torch import nn
class LinearRegression(nn.Module):
def __init__(self,in_features, out_features):
super().__init__()
self.w = nn.Parameter(torch.ones(in_features,1, dtype=torch.float32),requires_grad=True)
self.b = nn.Parameter(torch.ones(1, dtype=torch.float32),requires_grad=True)
def forward(self,X):
x = X@self.w + self.b
return x
model = LinearRegression(in_features=3,out_features=1)
for param in model.parameters():
print(param)
Parameter containing:
tensor([[1.],
[1.],
[1.]], requires_grad=True)
Parameter containing:
tensor([1.], requires_grad=True)
参数加入nn.Parameter后,就可以在model.parameters()中查看了
|
import torch
from torch import nn
# 定义模型
class Model(nn.Module):
def __init__(self, in_features=3, out_features=1):
super(Model, self).__init__()
self.linear1 = nn.Linear(in_features=in_features, out_features=out_features)
def forward(self, x):
out = self.linear1(x)
return out
model = Model(in_features=3,out_features=1)
model.parameters()
generator object Module.parameters at 0x7f31a1de5ee0
model.parameters
bound method Module.parameters of Model(
(linear1): Linear(in_features=3, out_features=1, bias=True)
)
for param in model.parameters():
print(param)
Parameter containing:
tensor([[ 0.3679, -0.2549, -0.5131]], requires_grad=True)
Parameter containing:
tensor([0.1661], requires_grad=True)
参数加入 |
|
模型改变,梯度下降法计算参数,其他不变
import torch
from torch import nn
class LinearRegression(nn.Module):
def __init__(self,in_features, out_features):
super().__init__()
self.w = torch.ones(in_features,1, dtype=torch.float32,requires_grad=True)
self.b = torch.ones(1, dtype=torch.float32,requires_grad=True)
def forward(self,X):
x = X@self.w + self.b
return x
def parameters(self):
params = [self.w,self.b]
return params
这种写法更原始一些,没有将参数加入nn.Parameter 这意味着 优化器 无法用了,因为model.parameters()没有参数了 optim = torch.optim.SGD(params=model.parameters(), lr=1e-2) 需要自定义一个优化器来更新参数 自定义模型参数与优化器验证
import torch
from torch import nn
class LinearRegression(nn.Module):
def __init__(self,in_features, out_features):
super().__init__()
self.w = torch.ones(in_features,1, dtype=torch.float32,requires_grad=True)
self.b = torch.ones(1, dtype=torch.float32,requires_grad=True)
def forward(self,X):
x = X@self.w + self.b
return x
def parameters(self):
params = [self.w,self.b]
return params
# 模型对象
model = LinearRegression(in_features=2, out_features=1)
# 损失函数
loss_fn = nn.MSELoss()
class Optim():
def __init__(self,params,lr):
self.params = params
self.lr = lr
def step(self):
# 更新参数
for param in self.params:
param.data -= self.lr * param.grad.data
def zero_grad(self):
"""清空梯度"""
for param in self.params:
param.grad.data.zero_()
# model.parameters()不是简单类型,传参的方式依然是引用
# 所以才能做到,修改它就是修改model中参数的效果,因为它们一个地址
optim = Optim(params=model.parameters(), lr=1e-2)
X = torch.tensor([[0.1,0.1]],dtype=torch.float32)
y = torch.tensor([[1]],dtype=torch.float32)
y_out = model(X)
loss_fn = nn.L1Loss()
loss = loss_fn(y_out,y)
loss.backward()
for param in model.parameters():
print(param)
"""
tensor([[1.],
[1.]], requires_grad=True)
tensor([1.], requires_grad=True)
"""
optim.step()
for param in model.parameters():
print(param)
"""
tensor([[0.9990],
[0.9990]], requires_grad=True)
tensor([0.9900], requires_grad=True)
"""
for param in model.parameters():
print(param.grad.data)
"""
tensor([[0.1000],
[0.1000]])
tensor([1.])
"""
optim.zero_grad()
for param in model.parameters():
print(param.grad.data)
"""
tensor([[0.],
[0.]])
tensor([0.])
"""
|
|
代码:更换了模型与优化器
from ai.datasets import load_boston
# 加载数据
X_train, y_train, X_test, y_test = load_boston()
# 标签shape处理,一个标签为一个向量
y_train = y_train.reshape((-1, 1))
y_test = y_test.reshape((-1, 1))
# 数据预处理
mean_ = X_train.mean(axis=0)
std_ = X_train.std(axis=0)
X_train = (X_train - mean_) / std_
X_test = (X_test - mean_) / std_
import torch
from torch import nn
# 数据打包
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
class MyDataset(Dataset):
"""自定义数据集
"""
def __init__(self, X, y):
"""超参
"""
self.X = X
self.y = y
def __getitem__(self, idx):
"""根据索引返回一对数据 (x, y)
"""
return torch.tensor(data=self.X[idx]).float(), torch.tensor(data=self.y[idx]).float()
def __len__(self):
"""数据总数
"""
return len(self.X)
# 训练集加载器
train_dataset = MyDataset(X=X_train, y=y_train)
# train_dataloader = DataLoader(dataset=train_dataset, batch_size=32, shuffle=True)
import torch
from torch import nn
class LinearRegression(nn.Module):
def __init__(self,in_features, out_features):
super().__init__()
self.w = torch.ones(in_features,1, dtype=torch.float32,requires_grad=True)
self.b = torch.ones(1, dtype=torch.float32,requires_grad=True)
def forward(self,X):
x = X@self.w + self.b
return x
def parameters(self):
params = [self.w,self.b]
return params
# 模型对象
model = LinearRegression(in_features=13, out_features=1)
# 损失函数
loss_fn = nn.MSELoss()
class Optim():
def __init__(self,params,lr):
self.params = params
self.lr = lr
def step(self):
# 更新参数
for param in self.params:
param.data -= self.lr * param.grad.data
def zero_grad(self):
"""清空梯度"""
for param in self.params:
param.grad.data.zero_()
# 优化器
# optim = torch.optim.SGD(params=model.parameters(), lr=1e-2)
optim = Optim(params=model.parameters(), lr=1e-2)
import numpy as np
test_dataset = MyDataset(X=X_test, y=y_test)
def get_loss(dataset, model=model, loss_fn=loss_fn, batch_size=128):
"""以整个数据集为基的损失评估
"""
dataloader = DataLoader(dataset=dataset, batch_size=batch_size, shuffle=False)
with torch.no_grad():
batch_loss = []
for X, y in dataloader:
y_out = model(X)
loss = loss_fn(y_out, y)
batch_loss.append(loss.item())
mean_loss = np.array(batch_loss).mean()
return mean_loss.round(4)
def trans(epoch,
batch_size=32,
train_dataset=train_dataset,
test_dataset=test_dataset,
model=model,
loss_fn=loss_fn,
optim=optim):
"""多轮训练
"""
train_dataloader = DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
for i in range(1,epoch+1):
print(f"...第{i}轮训练开始....\n")
# 一轮训练
count = 0
for X,y in train_dataloader:
count = count+1
y_out = model(X)
loss = loss_fn(y_out, y)
# 求当前参数在当前数据处的梯度
loss.backward()
if count%7==6:
print(round(loss.item(),4))
# 下降一次,就是朝着最优解的方向前进一步
optim.step()
optim.zero_grad()
epoch_loss_train = get_loss(dataset=train_dataset, model=model, loss_fn=loss_fn)
epoch_loss_test = get_loss(dataset=test_dataset, model=model, loss_fn=loss_fn)
print(f"第{i}轮训练,模型输出与训练集偏差:{epoch_loss_train},与测试集偏差:{epoch_loss_test}")
print("-------------------------\n")
trans(epoch=20)
def predict(X,model):
"""预测
"""
with torch.no_grad():
y_out = model(X)
return y_out
test_dataloader = DataLoader(dataset=test_dataset, batch_size=128, shuffle=False)
for X, y in test_dataloader:
y_pred = predict(X=X, model=model)
print(y_pred[:5],y[:5])
print(((y_pred - y) ** 2).mean())
break
输出
...第20轮训练开始....
26.8791
22.784
第20轮训练,模型输出与训练集偏差:25.0181,与测试集偏差:18.7029
-------------------------
tensor([[17.6071],
[25.1191],
[36.2995],
[18.5979],
[20.5758]]) tensor([[17.4000],
[23.9000],
[36.0000],
[12.1000],
[19.6000]])
tensor(18.7029)
预测效果 预测效果,与前面的两种方式在一个水平级别上 |
|
线性回归的输出是将一个维度的数据化为一个数,就是降了1维,因此输出维度是固定的
import torch
from torch import nn
class LinearRegression(nn.Module):
def __init__(self,in_features):
super().__init__()
self.w = nn.Parameter(torch.ones(in_features,1, dtype=torch.float32),requires_grad=True)
self.b = nn.Parameter(torch.ones(1, dtype=torch.float32),requires_grad=True)
def forward(self,X):
x = X@self.w + self.b
return x
model = LinearRegression(in_features=512) a = torch.randn(32,512) model(a).shape #torch.Size([32, 1]) 它的效果等同于一层线性连接 linear = nn.Linear(in_features=512,out_features=1,bias=True) linear(a).shape #torch.Size([32, 1]) |
|
|
|
|
回顾总结
标签没有做归一化处理
数据做了归一化,目的何在? 因为数据要代入模型,进行一层层神经网络的计算, 这个神经网络,目前根据无法处理大量的大于1的数据, 因此矩阵乘法具体到向量实际上是向量内积 向量内积是相乘再相加,如果数据都大于1, 乘法会让这些数据迅速变大,计算机就无法处理了
标签没有做归一化,为什么结果还算可以? 换句讲,标签为什么可以不做归一化? 因为标签代入的是损失函数, 它没有流入一层层的神经网络, 另外,它本身也不需要与谁相乘, 模型输出跟它比的是差异, 所以它不会产生什么数据爆炸 所以它不用做归一化
数据归一化后小于1,但训练后的参数未必全小于1
未必标签做归一化,那么标签又是连续值,是几十几百的数,
训练前随机初始化的模型参数几乎都是小于1的,
现在来看看训练后模型的参数
for param in model.parameters():
print(param)
Parameter containing:
tensor([[-7.4591e-01, 6.8696e-01, -2.9462e-01, 1.0525e+00, -1.1340e+00,
3.1784e+00, -2.3888e-03, -2.3702e+00, 1.1473e+00, -3.9150e-01,
-1.7936e+00, 9.1111e-01, -3.7042e+00]], requires_grad=True)
Parameter containing:
tensor([22.8020], requires_grad=True)
有正有负,有小于1的,也有大于1的,比如
3.1784e+00,...,-3.7042e+00,
偏置就更不用说了,是 22.8020
这也是偏置不需要归一化的另外一个原因,
并且标签未必就非得是One Hot编码那种非0即1的情况,
也可以是几十几百的数...
模型训练时,自会调整参数,使其逼近标签!
关键的两个环节/步骤
全连接,更确切地说是线性变换, 以近似等价的方式 模拟/或者说是给出了 事物从一个状态到另外一个状态的公式 梯度下降法: w = w - learning_rate*w.grad 以原函数的导函数可反映 其正负变化趋势 的特点/性质, 又加入一定微分/积分的思想,增加了学习率这个参数learning_rate=0.001 再加上计算机强大的遍历计算的能力, 才有了现在的效果,不完美,但能解决一些实际问题 事物转换有其本身的结构/规律,或者不止一个, 但我们是一个都不知道... 线性变换是能近似地描述事物两个状态之间的规律, 但也不能所有规律/结构,都用一个全连接来表示,这太粗糙了... 猜不道事物规律的全部,可以局部猜个大概结构, 比如盲人摸象,摸着腿像柱子,摸着肚子像墙, 就可以建立一个更适合描述柱子的线性变换,和一个更贴切描述墙的线性变换 要比直接一个线性变换去表示大象更好一些
框架的核心
就是pytorch框架工作的关键点:loss.backward() 从损失函数开始对模型参数求导并计算梯度... 这个功能是无法重写的,这是框架的意义所在,或者说是不可替代的环节,其他的都可用python+numpy实现
参考