ibm数据集
/wks/python/jupyter/dl_kejian/ibm-aml
|
|
|
|
|
|
|
relu
|
np.array([0 if ele < 0 else ele for ele in x]) 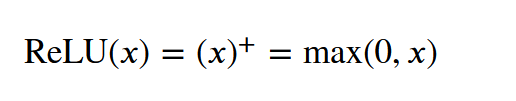
import numpy as np
import torch
from torch import nn
from torch.nn import functional as F
class Activate(object):
def __init__(self):
pass
@staticmethod
def relu(X):
X = np.array(X)
shape = X.shape
X = X.reshape(-1)
x = np.array([0 if x < 0 else x for x in X])
x = x.reshape(shape)
return x
@staticmethod
def relu2(X):
X = torch.tensor(data=X,dtype=torch.float64)
return X.relu()
@staticmethod
def relu3(X):
X = torch.tensor(data=X)
return F.relu(input=X,inplace=True)
np.random.seed(73)
A=np.random.randn(7,3)
# print(A)
"""
[[ 0.57681305 2.1311088 2.44021967]
[ 0.26332687 -1.49612065 -0.03673531]
[ 0.43069579 -1.52947433 -0.73025968]
[ 1.05131524 1.61979267 -1.60501337]
[ 0.33100953 -0.21095236 0.2981767 ]
[-1.14607352 0.57536202 -0.36390663]
[ 0.03639919 -0.52056399 -0.01576433]]
"""
# B = Activate.relu(X=A)
# print(B)
"""
[[0.57681305 2.1311088 2.44021967]
[0.26332687 0. 0. ]
[0.43069579 0. 0. ]
[1.05131524 1.61979267 0. ]
[0.33100953 0. 0.2981767 ]
[0. 0.57536202 0. ]
[0.03639919 0. 0. ]]
"""
# B = Activate.relu2(X=A)
# print(B)
"""可以看出torch.relu()只保留了四位有效数字
tensor([[0.5768, 2.1311, 2.4402],
[0.2633, 0.0000, 0.0000],
[0.4307, 0.0000, 0.0000],
[1.0513, 1.6198, 0.0000],
[0.3310, 0.0000, 0.2982],
[0.0000, 0.5754, 0.0000],
[0.0364, 0.0000, 0.0000]], dtype=torch.float64)
"""
B = Activate.relu3(X=A)
print(B)
"""F.relu同样改变了数据的精度
tensor([[0.5768, 2.1311, 2.4402],
[0.2633, 0.0000, 0.0000],
[0.4307, 0.0000, 0.0000],
[1.0513, 1.6198, 0.0000],
[0.3310, 0.0000, 0.2982],
[0.0000, 0.5754, 0.0000],
[0.0364, 0.0000, 0.0000]], dtype=torch.float64)
"""
|
以0为分界点,
- 低于0的数据为0,直接就不用算了,因为任何数乘以0就是0
- 高于0,则导数为1,链式求导中,激活函数不会放大或缩小导函数中的值了,导函数值的大小只受参数变量的影响
- 0与1是极其特殊的两个数字,在这个简单的不能再简单的函数中,同时出现了,也有点神乎其技的感觉...
计算量低,效果也并不比sigmoid差,极受工程青睐
- 主要是当参数成千上万时,会有亿万个激活函数在运行
- 这就要求函数越简单越好
缺点是当x小于0时,直接置为0,在理论上好像不太好 |
|
|
|
|
|
|
nn.PReLU
nn.PReLU(num_parameters=10, init=0.25)
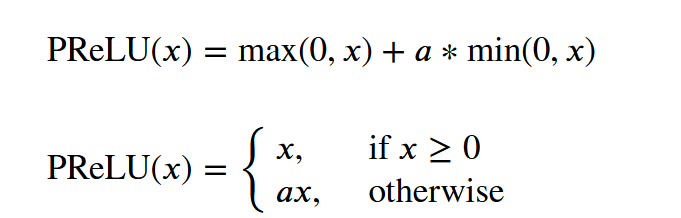
nn.PReLU(): a 可学习,根据数据变化而变化
PReLU(𝑥)=max(0,𝑥)+𝑎∗min(0,𝑥)
其中a是可学习的参数/权重,
当x大于等于0时,取x,
当x小于0时,是完全舍去还是按比例保留,通过学习而定
超参数:
num_parameters (int):输入数据的通道数
init (float):超参数a的初始化值,默认0.25
示例:
self.layer = nn.Sequential(
nn.Conv2d(in_channels=3,
out_channels=10,
kernel_size=3,
stride=1,
padding=1),
nn.BatchNorm2d(num_features=10),
nn.PReLU(num_parameters=10, init=0.25),
nn.MaxPool2d(kernel_size=2, stride=2)
)
Rrule
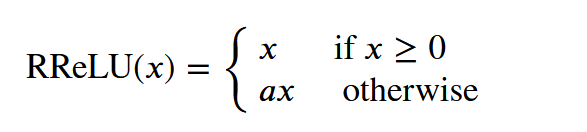
nn.RReLU()
RReLU中的 a是一个在 一个给定的范围内 随机抽取的值。
sigmoid
import numpy as np
from matplotlib import pyplot as plt
def linear(x):
return 3 * x - 7
x = np.linspace(start=-10, stop=10, num=50)
plt.plot(x, linear(x))
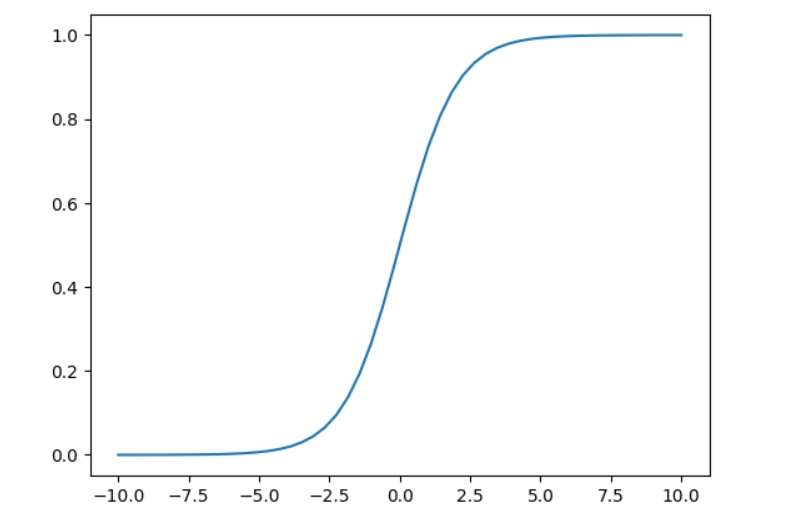
def sigmoid(x):
return 1 / (1 + np.exp(-x))
plt.plot(x, sigmoid(x))
|
sigmoid函数将数据映射到[0,1]
- 对应概率,可以将数据转换为概率
- 也有类似计算机非0即1的意味
- e函数求导方便
- 对定义域无限制,可以是任何实数,即不管数据范围如何,都到映射到[0,1]
缺点
- 指数函数在计算机中比线性函数计算量大
- 对于分布来说,以0为中心更好一些
- 当数据比较大时,sigmoid函数的梯度会变得很小
- 深度学习中求导是链式示求导,
- 即损失函数在某个参数变量处的导数值是n个导函数的值相乘
- 本身就很小,再相乘,就更小了
- 最后梯度就消失了,w=w-lr*w.grad梯度下降变为梯度不变
- 如此参数就无法更新了,模型就训练不下去了
|
|
|
|
|
|
|
tanh
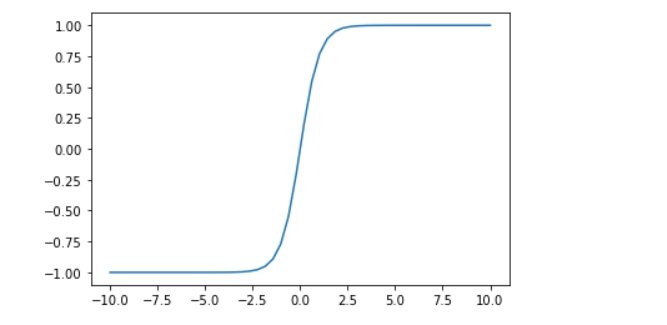
def tanh(x):
return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
|
双曲正切函数,相比sigmoid函数
- 数据以0为中心,[-1,1]
缺陷
- 同sigmoid一样,但它又不像sigmoid函数那样可以类比概率
- 所以应用的场景很少,基本不用了
|
|
|
|
|
|
|
参考
神经网络】神经元ReLU、Leaky ReLU、PReLU和RReLU的比较