概率计算
|
(y == i).mean()
import numpy as np
y = np.array([1,1,2,2,3])
y_prob = {}
y_set = set(y)
for i in y_set:
y_prob[i] = (y == i).mean()
y_prob
y_prob[i] = (y == i).mean() 该代码的特点: 思想一致:都是在计算离散变量的概率 高性能计算:效率高,计算速度快 效果一致:与理论上的结果一致 标签概率 标签是类别,类别的概率,即离散变量的概率计算,是数数 一类的个数/总个数 (y == i).mean() - y == i 真假列表 ,0或1 - y是一个向量,i是一个数值,会将向量的每个元素与i进行比较 - mean,1的个数加起来/总个数 ,即用一个函数mean替换了count/sum, |
|
P(y1|(x1,x2,x3)) = P(x1|y1) P(x2|y1) P(x3|y1)P(y1) P(y1|x) = P(y1|(x1,x2,x3)) = P(x1|y1) P(x2|y1) P(x3|y1)P(y1) x1,x2,x3是不同的特征,自有其特点/特性, 有不同的均值,标准差, 这里假设 - 所有特征相互独立 - 所有变量默认为连续变量 - 连续变量按概率密度求概率,自带归一化处理 - 因此,已经将他们拉到标准正态的维度上进行处理了 同时这里也有工程近似 - 该公式来自贝叶斯,对于既定的样本x,它的概率是定值,因为概率不像频率,本来就是定值 - 之所以抹去p(x),是相对y1,y2,...,yn来说的,目的在于取出它们中的最大值 - 而公式中的分母都是p(x),故可以抹去 |
|
X[y==0] import numpy as np X = np.arange(21).reshape((7,3)) X
array([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11],
[12, 13, 14],
[15, 16, 17],
[18, 19, 20]])
y = np.array([0,1,0,1,0,0,1])
X[y==0]
array([[ 0, 1, 2],
[ 6, 7, 8],
[12, 13, 14],
[15, 16, 17]])
X[y==1]
array([[ 3, 4, 5],
[ 9, 10, 11],
[18, 19, 20]])
----------------------------------------------------------------- |
|
|
生成一组数
import numpy as np
from matplotlib import pyplot as plt
x = np.linspace(start=-10, stop=10, num=50)
|
|
|
|
|
|
|
|
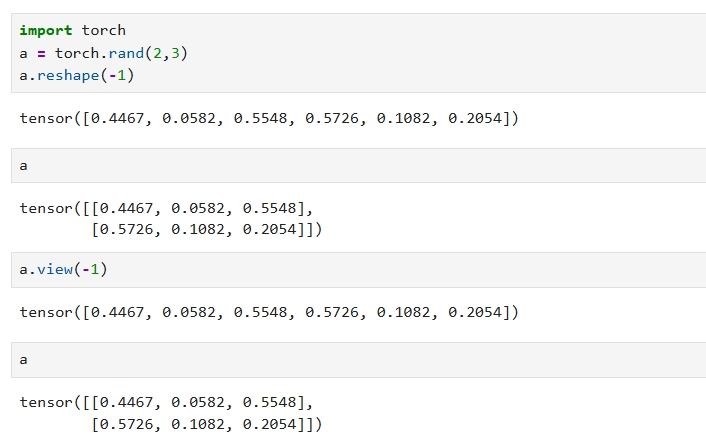
转为1维
label = np.array(y_train)
if label.ndim > 1:
label = label.ravel() # 转换为一维数组
label.shape
ravel 英/ˈrævl/ 美/ˈrævl/
vt. 使…缠绕;使更复杂;使更纷乱
n. 缠绕;(绳,织物等)散开的一端;错杂
|
|
|
|
|
|
|
|
参考文章