离群点（Outlier）或异常值（Anomaly）
在统计学中指的是那些与数据集中的其他数据点显著不同的数据点。

这些点可能由于测量错误、数据输入错误、自然变异或真实存在的罕见事件而产生。
离群点可能包含重要的信息，也可能只是数据集中的噪声。
    

 
在处理数据时，识别和处理离群点是非常重要的。
离群点可能会对统计分析和机器学习模型的准确性产生负面影响，

因为它们可能不符合数据的一般模式或分布。
因此，在进行分析之前，通常需要检测并处理这些离群点。

处理离群点的方法包括

 
删除：如果离群点是由于测量错误或数据输入错误产生的，可以将其从数据集中删除。

转换：通过某些数学变换（如对数变换）来减少离群点对分析的影响。

单独分析：对离群点进行单独分析，以了解它们是否代表某种重要的、罕见的事件或模式。

使用稳健的统计方法：选择那些对离群点不太敏感的统计方法或机器学习算法进行分析。

 
总之，离群点是数据集中与其他数据点显著不同的点，
它们可能包含重要信息，也可能只是噪声。
在处理数据时，需要仔细考虑如何处理这些离群点，以确保分析的准确性和可靠性。
    

 
基于Z分数的方法：
计算数据点的Z分数。
如果Z分数的绝对值大于3（或2，根据具体情况而定），则该数据点可能被视为离群点。

 
基于四分位数的方法：
计算数据的第一四分位数（Q1）和第三四分位数（Q3）。
计算IQR（四分位距）= Q3 - Q1。
如果数据点小于Q1 - 1.5 * IQR或大于Q3 + 1.5 * IQR，则该数据点可能被视为离群点。

 
基于箱线图的方法：
箱线图是一种用于显示数据分布情况的图表，其中箱体的上下边界分别表示数据的上四分位数和下四分位数。
箱线图外的点（即超出箱体上下边界的点）通常被视为离群点。

 
基于模型的方法：
使用统计模型（如回归模型）来拟合数据。
根据模型的残差来判断数据点是否为离群点。
如果某个数据点的残差远大于其他数据点的残差，则该数据点可能被视为离群点。

 
基于密度的方法：
估计数据的密度分布。
如果某个数据点位于密度分布的尾部（即密度很低），则该数据点可能被视为离群点。

定义

 
Z值(Z-score)是一个数据点与平均值的差再除以标准差的结果，
表示该数据点与平均值的相对位置。

数据点的Z分数（Z-score）计算是一个在统计学中广泛使用的方法，

用于衡量一个数据点与平均值的偏离程度，

并将其转化为 标准正态分布中的位置。
    

用途

 
Z值用于标准化数据，使其具有统一的度量标准，便于比较和分析。

在正态分布中，Z值还可以用于计算数据点出现的概率。

其计算公式为：

   
Z = (X - μ) / σ

其中：
Z 表示Z分数。
X 表示某一具体的数据点。
μ 表示数据集的总体均值或样本均值（在实际应用中，如果总体均值未知，则常用样本均值作为估计）。
σ 表示数据集的总体标准差或样本标准差。
    

 
Z分数的正负表示数据点相对于均值的位置，正值表示高于均值，负值表示低于均值。

Z分数的绝对值越大，表示数据点与均值的偏离程度越大。

在标准正态分布中，Z分数可以用来查找数据点出现的概率。

在实际应用中，Z分数常用于判断数据点是否为异常值。
一般而言，Z分数大于3或小于-3的数据点可以被认为是异常值。

 
假设有50名随机选择的志愿者参加了智商测试，
其中一名志愿者海伦（Helen）的得分为74分（X），平均分数为62分（μ），标准偏差为11分（σ）。
为了判断海伦的表现在测试中的位置，我们可以计算她的Z分数：

Z = (74 - 62) / 11 = 1.09

这意味着海伦的智商测试得分比平均分高出了大约1个标准差的位置。

 
注意
在计算Z分数时，应确保使用的均值和标准差与数据点X来自同一数据集。

如果数据集很大或总体均值和标准差已知且稳定，则可以使用总体均值和标准差进行计算。
否则，通常使用样本均值和标准差作为估计。

Z分数的计算依赖于数据服从正态分布或近似正态分布的假设。
如果数据分布严重偏离正态，则Z分数的解释可能受到限制。

基于密度的方法（Kernel Density Estimation, KDE）

 
在计算一个分布的密度时，
主要依赖于对 空间中数据点 分布密集程度 的量化。
这种方法在统计学、数据挖掘、空间分析等多个领域都有广泛应用。

 
核密度估计法是一种使用事件的空间密度分析表示空间点模式的方法。
其基本思想认为地理事件可以发生在空间的任何位置上，但不同位置上事件发生的概率不一样。
点密集的区域事件发生的概率高，点稀疏的区域事件发生的概率低。

计算方法：
对于连续型随机变量X，核密度估计通过选择一个核函数（如高斯核）来平滑数据点，
从而估计出整个空间的密度分布。
具体地，对于给定的数据点集合{x1,x2,...,xn}，核密度估计在点x处的密度估计值为：

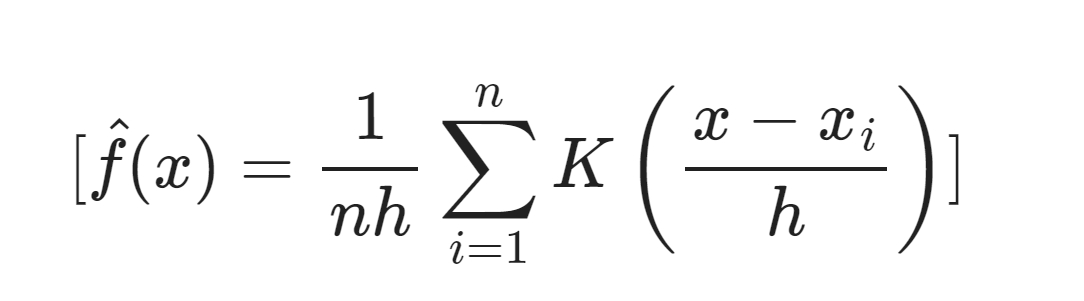
K是核函数，h是带宽参数，用于控制估计的平滑程度

 
[\hat{f}(x) = \frac{1}{nh} \sum_{i=1}^{n} K\left(\frac{x - x_i}{h}\right)]

优点：
能够提供平滑的密度估计，有助于揭示数据的潜在结构。
不依赖于数据的直方图分组，结果更加稳定。

缺点：
带宽参数的选择对结果有较大影响，需要仔细调整。
计算复杂度较高，特别是对于大规模数据集。
    

 
样方分析法通常用于空间点模式分析，通过将研究区域划分为规则的正方形网格区域，并统计落入每个网格中点的数量来计算密度。

计算步骤：

将研究区域划分为若干规则的正方形网格。
统计每个网格中点的数量，得到每个网格的密度估计值。
可选地，将观测得到的频率分布与理论上的随机分布（如泊松分布）进行比较，以判断点模式的类型。
优点：

实现简单，易于理解。
适用于大规模数据集的空间分布分析。
缺点：

网格大小的选择对结果有较大影响。
可能会忽略点之间的空间关系。
    

基于密度的聚类算法（如DBSCAN）

 
虽然DBSCAN主要用于聚类分析，但它也基于密度的概念来识别数据中的簇。

核心思想：
DBSCAN通过定义两个参数ε（邻域大小）和MinPts（最小点数）来识别核心点、边界点和噪声点。
核心点是在其ε-邻域内至少包含MinPts个点的点。
通过连接由核心点组成的密度可达的点集来形成簇。

优点：
能够识别任意形状的簇。
对噪声和异常值不敏感。

缺点：
参数ε和MinPts的选择对结果有较大影响。
对于密度差异很大的数据集，可能需要调整参数以获得满意的聚类效果。

 
数据的直方图分组是指将数据按照一定的规则或标准划分成若干个组别，
以便于通过直方图的形式展示数据的分布情况。

直方图是一种统计报告图，由一系列高度不等的纵向条纹或线段表示数据分布的情况，
横轴通常表示数据类型或组别，纵轴表示各组的频数或频率。

    

分组的目的

 
直方图的分组旨在将连续的数据离散化，
通过统计每个组别内的数据频数或频率，以图形的形式直观地展示数据的分布特征，
如中心位置、分散程度和分布形状等。

 
确定极差：
首先，需要找出数据中的最大值和最小值，计算极差（最大值与最小值之差）。
极差反映了数据的变动范围。

确定组数：组数的确定可以基于经验公式或根据数据的实际情况进行调整。
一种常用的方法是使组数约等于样本容量的平方根。
此外，还可以参考斯特吉斯（Sturges）公式或斯科特（Scott）公式等来确定组数。

确定组距：组距是指相邻两组之间的间隔。
组距的大小直接影响直方图的形状和数据的展示效果。
组距可以通过极差除以组数来计算，并通常取为整数或易于计算的数值，以便于分组和统计。

确定分点：根据确定的组距和数据的实际情况，划分出各个组别的界限值（即分点）。
分点的确定应确保每个数据点都能被正确地归入某个组别中。

频数统计：最后，统计每个组别内的数据频数或频率。
频数是指某组别内数据的个数，而频率则是频数与总数据量的比值。

    

 
分组不宜过多或过少：
分组过多会导致直方图过于复杂，难以看清数据的分布特征；
分组过少则可能掩盖数据的细节信息。
因此，需要根据数据的实际情况和展示需求来确定合适的组数。

组距应相等：
在大多数情况下，为了保持直方图的对称性和美观性，各组距应保持相等。
但在某些特殊情况下，如数据分布极不均匀时，也可以采用不等距分组的方法。

考虑数据的实际情况：
在确定分组方法和参数时，需要充分考虑数据的实际情况和展示需求。
例如，对于偏态分布的数据，
可能需要采用特殊的分组方法来更好地展示其分布特征。