交叉熵使用示例
文本类
文本拆分为单词,单词转化为索引,进而句子转化为索引向量 入模型时,需要将索引向量转化为矩阵,即每个单词化为一个向量 预测时,又需要将向量转化为索引,进而与字典中的单词对应
在索引转向量时,是随机的, 一个随机的向量反向对应索引时,偏差就比较大 可以在入模前就训练一批向量参数,使 索引 -- 向量参数 -- 索引 之间有一一对应关系 一个索引,比如index=2,对应的就是向量a, 如果得到一个向量a,就立即确定它唯一对应index=2
进一步简化,直接求解一个参数矩阵,func(index) ~ func(param_mat) ~ one hot向量 ~ 最大值的位置索引 模型输入的是index,param_mat即包含了index的信息,又包含了模型的规律,还能通过func转化为one hot向量
文本类交叉熵举例
import torch
from torch import nn
dict_count = 3 #有三个单词,索引为0,1,2
seq_len = 5
batch_size = 2
#`low` (inclusive) and :attr:`high` (exclusive).
data = torch.randint(low=0, high=dict_count, size=(batch_size,seq_len))
data
tensor([[0, 0, 2, 1, 2],
[0, 2, 0, 0, 0]])
label = data label.shape torch.Size([2, 5]) #对X进行编码 embed = nn.Embedding(num_embeddings=dict_count, embedding_dim=dict_count, padding_idx=0) X = embed(data)
现在求X与label之间的偏差
注意X与label的shape并不一样,交叉䊞能自动处理这一点, 但第1维必须是一样的,最多2维,高于2维的必须展平 认为X[0]的向量,对应y[0]转化后的One hot向量
X = X.reshape(-1,dict_count)
label = label.reshape(-1)
print(X.shape,label.shape) #torch.Size([10, 3]) torch.Size([10])
loss_fn = nn.CrossEntropyLoss()
loss = loss_fn(X,label)
loss
tensor(1.3767, grad_fn=NllLossBackward0)
交叉熵API说明
|
torch.nn.CrossEntropyLoss()
This criterion computes the cross entropy loss between input logits and target.
criterion 美 /kraɪˈtɪriən/ n.标准;(评判或作决定的)准则;原则
Init signature:
nn.CrossEntropyLoss(
weight: Optional[torch.Tensor] = None,
size_average=None,
ignore_index: int = -100,
reduce=None,
reduction: str = 'mean',
label_smoothing: float = 0.0,
) -> None
使用 loss_fn=nn.CrossEntropyLoss() loss = loss_fn(input,target) input: 输入 target: 标签 input input没啥可注意的,重点是后面的target unnormalized 非归一化;非标准的 The `input` is expected to contain the unnormalized logits for each class (which do `not` need to be positive or sum to 1, in general). `input` has to be a Tensor of size :math:`(C)` for unbatched input, :math:`(minibatch, C)` or :math:`(minibatch, C, d_1, d_2, ..., d_K)` with :math:`K \geq 1` for the `K`-dimensional case. The last being useful for higher dimension inputs, such as computing cross entropy loss per-pixel for 2D images. 交叉熵的输入(input)的shape,可以是 [特征维度],没有批次的维度,只有特征的维度, 言外之意就是一行数据,一个样本, 这个特征维度就是模型的最后一层的维度,也是标签的维度 比如,模型输出[0.1,0.9] 跟对应的标签[0,1]求损失, 这是标准的,也是直接按数学理论转换过来的求交叉熵的格式 [batch_size, C],这说明交叉熵可以按批次求损失 [batch_size,C,H,W] 这是典型的2维图像的格式, 直接将这个格式作为交叉熵的损失函数也是可以的 target
indices 英/ˈɪndɪsiːz/ 美/ˈɪndɪsiːz/ (index 的复数形式之一);索引;标志,迹象;
The `target` that this criterion expects should contain either:
- Class indices in the range :math:`[0, C)` where :math:`C` is the number of classes;
假设特征数C=3,那么
for i in range(3):
print(i)
输出:
0
1
2
意思是说,如果标签类别有3,那么标签的编码应该是[0,1,2]
这就是后面的 索引标签计算交叉熵
|
|
loss = loss_fn(y_pred, y) y是1维列表
import os
from tpf import pkl_save,pkl_load
BASE_DIR = "/wks/datasets/hotel_reader"
file_path = os.path.join(BASE_DIR,'data_pkl/word.pkl')
X_train,y_train,X_test,y_test,words_set,word2idx,idx2word = pkl_load(file_path)
# 字典长度
dict_len = len(words_set)
# 序列长度
seq_len = 512
# 训练集
X_train1 = []
for x in X_train:
temp = x + ["<PAD>"] * seq_len
X_train1.append(temp[:seq_len])
# 测试集
X_test1 = []
for x in X_test:
temp = x + ["<PAD>"] * seq_len
X_test1.append(temp[:seq_len])
"""
索引向量化
"""
# 训练集向量化
X_train2 = []
for x in X_train1:
temp = []
for word in x:
idx = word2idx[word] if word in word2idx else word2idx["<UNK>"]
temp.append(idx)
X_train2.append(temp)
# 测试集向量化
X_test2 = []
for x in X_test1:
temp = []
for word in x:
idx = word2idx[word] if word in word2idx else word2idx["<UNK>"]
temp.append(idx)
X_test2.append(temp)
"""
构建数据集
"""
import numpy as np
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
import torch
from torch import nn
from torch.nn import functional as F
class MyDataSet(Dataset):
def __init__(self, X=X_train2, y=y_train):
self.X = X
self.y = y
def __len__(self):
return len(self.X)
def __getitem__(self, idx):
x = self.X[idx]
y = self.y[idx]
return torch.tensor(data=x).long(), torch.tensor(data=y).long()
train_dataset = MyDataSet(X=X_train2, y=y_train)
train_dataloader = DataLoader(dataset=train_dataset, shuffle=True, batch_size=128)
test_dataset = MyDataSet(X=X_test2, y=y_test)
test_dataloader = DataLoader(dataset=test_dataset, shuffle=False, batch_size=256)
train_dataset[0][0][:7]
tensor([ 5004, 10135, 20586, 9530, 16808, 14513, 9530])
train_dataset[0][1]
1
for X,y in test_dataloader:
print(X.shape,y.shape)
break
torch.Size([256, 512]) torch.Size([256])
二分类问题中,loss = loss_fn(y_pred, y), y是1维列表
|
|
标签y是long类型,类别是用整数表示的
"""
构建数据集
"""
import numpy as np
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
import torch
from torch import nn
from torch.nn import functional as F
class MyDataSet(Dataset):
def __init__(self,X,y):
"""
构建数据集
"""
self.X = X
self.y = y.reshape(-1)
# self.y = y.reshape(-1,1)
def __len__(self):
return len(self.X)
def __getitem__(self, idx):
x = self.X[idx]
y = self.y[idx]
return torch.tensor(data=x).float(), torch.tensor(data=y).long()
|
|
|
|
|
one hot标签计算交叉熵
import torch from torch import nn import numpy as np input = torch.tensor([0,0,1],dtype=torch.float32,requires_grad=True) # target = torch.tensor(2,dtype=torch.long) # 0.5514 target = torch.tensor([0,1,0],dtype=torch.float32) # 1.5514 # target = torch.tensor(0,dtype=torch.long) # 1.5514 loss = nn.CrossEntropyLoss() output = loss(input, target) output.backward() output tensor(1.5514, grad_fn=DivBackward1)
索引标签计算交叉熵
import torch from torch import nn import numpy as np input = torch.tensor([0,0,1],dtype=torch.float32,requires_grad=True) # target = torch.tensor(2,dtype=torch.long) # 0.5514 # target = torch.tensor([0,1,0],dtype=torch.float32) # 1.5514 target = torch.tensor(0,dtype=torch.long) # 1.5514 loss = nn.CrossEntropyLoss() output = loss(input, target) output.backward() output tensor(1.5514, grad_fn=NllLossBackward0) 该例表明,交叉熵在输入的标签是整数时,默认将其转换为one hot标签,无须再手工转换,其效果与One Hot标签一致
批次损失计算
reduction: str = 'mean'
每个样本与标签都有一个损失, 如果输入的是批次,交叉熵默认情况下求出的损失是批次样本损失的均值 reduce参数已废弃,看reduction,其默认值为mean batch_size = Nwhere :math:`x` is the input, :math:`y` is the target, :math:`w` is the weight, :math:`C` is the number of classes, and :math:`N` spans the minibatch dimension
批次损失计算
import torch from torch import nn import numpy as np # loss 1.0514 x = [[0,0,1],[0,0,1]] y = [[0,1,0],[0,0,1]] # 1.5514 x = [[0,0,1]] y = [[0,1,0]] # 0.5514 x = [[0,0,1]] y = [[0,0,1]] input = torch.tensor(x,dtype=torch.float32,requires_grad=True) # target = torch.tensor(2,dtype=torch.long) target = torch.tensor(y,dtype=torch.float32) # target = torch.tensor(0,dtype=torch.long) loss = nn.CrossEntropyLoss() output = loss(input, target) output.backward() output (0.5514+1.5514)/2 = 1.0514 每个样本与标签都有一个损失, 如果输入的是批次,交叉熵默认情况下求出的损失是批次样本损失的均值
转成索引标签也一样
import torch from torch import nn import numpy as np # loss 1.0514 x = [[0,0,1],[0,0,1]] y = [[0,1,0],[0,0,1]] y = [1,2] #按one hot编码的方式,这时共有3个类别 input = torch.tensor(x,dtype=torch.float32,requires_grad=True) target = torch.tensor(y,dtype=torch.long) loss = nn.CrossEntropyLoss() output = loss(input, target) output.backward() output tensor(1.0514, grad_fn=NllLossBackward0)
交叉熵公式
借pytorch交叉熵的API文档推一下交叉熵的数学公式
Probabilities for each class; useful when labels beyond a single class per minibatch item are required, such as for blended labels, label smoothing, etc. The unreduced (i.e. with :attr:`reduction` set to ``'none'``) loss for this case can be described as:
.. math::
\ell(x, y) = L = \{l_1,\dots,l_N\}^\top, \quad
l_n = - \sum_{c=1}^C w_c \log \frac{\exp(x_{n,c})}{\sum_{i=1}^C \exp(x_{n,i})} y_{n,c}
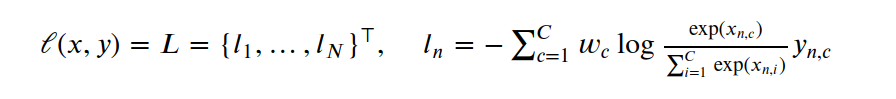
where :math:`x` is the input, :math:`y` is the target, :math:`w` is the weight, :math:`C` is the number of classes, and :math:`N` spans the minibatch dimension as well as :math:`d_1, ..., d_k` for the `K`-dimensional case.
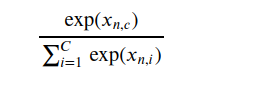
上图就是softmax,对x中的每个元素进行指数运算,然后再除以指数的和, 其和为1, 它真正要表达的意思是,概率和为1, 比如,二分类问题,类型共有两个,[发生,不发生],[是,否], 总类别个数为C,这是全集, 一个事物不在这个类型,就必定在那个类别中 softmax处理的对象是模型的输出,为什么不对标签这么处理? 因为标签本身很固定,确切地说是你亲自编码的,它属于哪个类别是铁板钉钉的事,一算就知 而模型的输出那可真是乱七八糟,五花八门, 你期望模型输出0.9,期望它接近你的标签1, 但实际上它可能输出的是-0.7,直接就违反了概率要大于1的理论基础啊 怎么办? 常用的办法是用softmax处理一下, 将模型在各个类别上的差异,转化为符合概率理论的差异
xn是一个向量,指批次中第n个样本,它有C个维度(C是类别个数), yn就是标签,也是一个向量,也有C个维度(C是类别个数), 特别地,如果对标签使用one hot编码(实际上,通常,就是这么做的) yn中只有一个维度为1,其他维度皆为0 比如,二分类问题,类型共有两个,one hot编码是下面这样的 发生用[1,0]向量表示,不发生用[0,1]向量表示 二者在距离上完全一样,没有差异 0乘以任何数还是0,C维度的计算,只算标签为1的那个维度就可以了, 同时先不考虑权重的问题,上面的公式简化为:
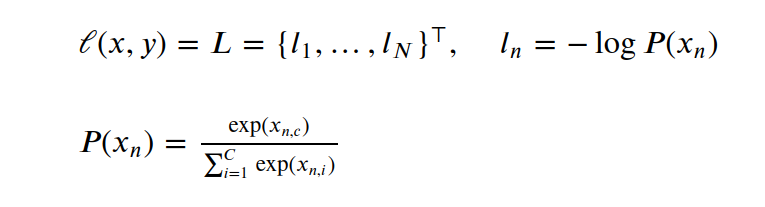
如此,每个样本与标签的交叉熵损失,转化为模型输出的 信息量 训练的目的转化为,让模型输出的信息量,越来越小, 小到很容易就分出是哪个类别时,就达到目的了 xn是一个向量,xnc指与yn标签1所在索引对应的x的值, 因为其他位置都是与0相乘,乘完就消失了 因此P(xn)就 只是 其中与标签1对应索引位置的x占xn的概率
交叉熵权重
It is useful when training a classification problem with `C` classes. If provided, the optional argument :attr:`weight` should be a 1D `Tensor` assigning weight to each of the classes. This is particularly useful when you have an unbalanced training set.
参考