nn.NLLLoss

NLLLoss: negative log likelihood loss,负对数似然损失

 
这个函数是相对 交叉熵来说的，先回顾一下前面说的交叉熵最后的简化形式

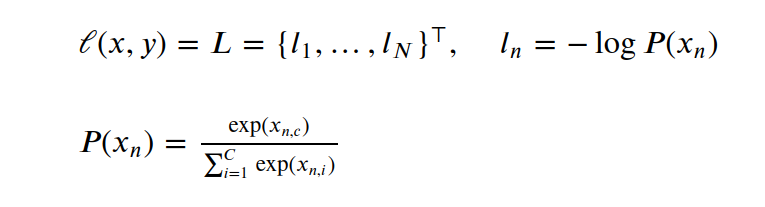
负对数

 
负对数说的就是这个简化后的函数 -logx， 这是一个以2为底的对数函数

y = -logx的函数曲线，这是一个单调递减的函数

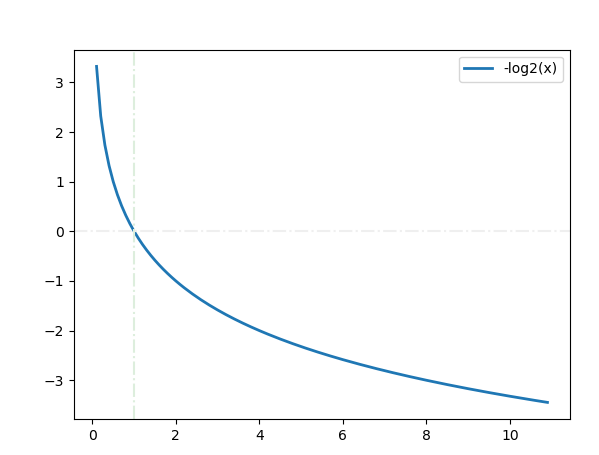
负对数的简化与似然

 
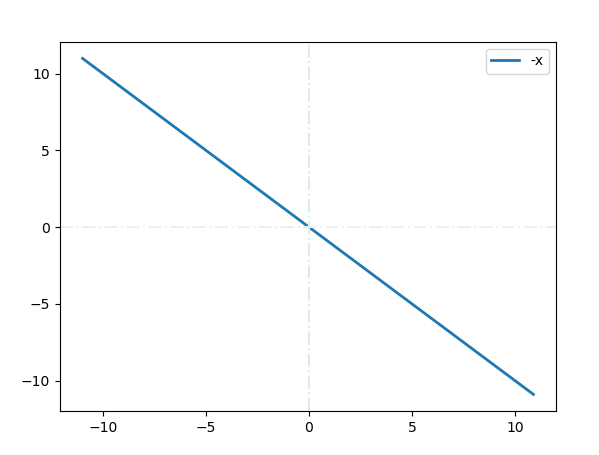
y = -logx 
简化为
y = -x 

单调性一致，
当x从负变为正时，y从大不断地变小 
如果使用softmax将x约束到(0,1)的范畴，那么Y=-x的最小值就是-1,即损失函数不断在逼近-1 

似然，通常指概率未定，样本确定
这里将x映射到(0,1)的概率后，
这个函数中唯一的变量就是模型输出的概率x了，
所以，称之为似然函数

标签的类型与one hot编码

 
标签=[0,2]
这种写法，意味着有三个类别 

类型个数为C，那么标签的取值为[0,C-1] 
标签中的每个值实为索引下标，对应one hot编码 
[0,0,1]  2
[0,1,0]  1
[1,0,0]  0 

数据x与模型输出x

 
数据x的特征未必就是标签的类别数
但
模型输出x的特征就是标签的类别数
因为特征维数相等，所以二者/这两个分布 才可以设计一个函数求损失/偏差 

更准确的说，是要与标签求损失，所以模型的输出特征数就定为了标签的类别数

模型输出x的正与负，大与小

 
期望模型输出x接近标签,
但训练之初，x必有负值，
x从负到正的过程，会让损失越来越小 
x从小到大的过程，也会让损失越来越小 
因为y = -x是一个单调递减函数 

负对数似然损失公式

 
y = -x

没错，“负对数似然损失”这么一个高大上的名字，其公式就是y=-x 

上面是为帮助理解，个人写的铺垫，下面是正式且标准的官方公式

 
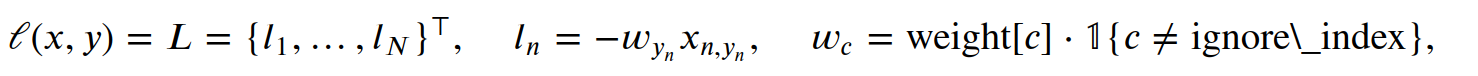
where 
:math:`x` is the input, 
:math:`y` is the target, 
:math:`w` is the weight, and
:math:`N` is the batch size. If :attr:`reduction` is not ``'none'``
    (default ``'mean'``), then

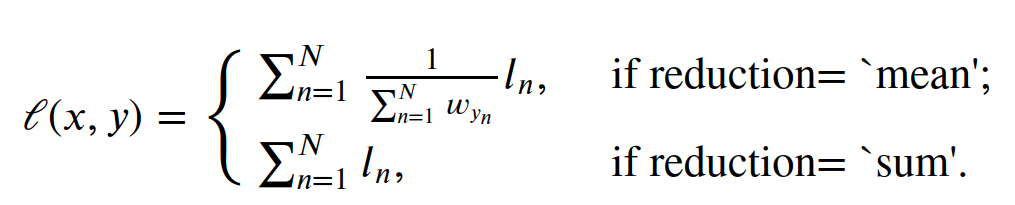
weight

 
weight (Tensor, optional): a manual rescaling weight given to eachclass. 
If given, it has to be a Tensor of size `C`. 
Otherwise, it is treated as if having all ones.

权重，默认是1,当它为1时，权重之和就是特征的个数，
此时，ln/sum(w),实际上是一个样本的损失/该样本 同一类别 所有批次 权重的和 
这是一个批次，再

 
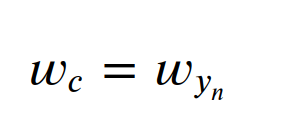
yn是什么,yn是模型输出特征的索引下标
标签y=[0,2]，这里有两个样本，类别数3
n=1时，
yn=y1=2，但这个2实际上是指索引2，第三个类别，
索引2,对应的是x的第3个值，即x[2] 

批次有n个，那么标签y为什么也刚好有n个
为什么有yn，
标签y=[0,2]，一个标签就是一个样本，所以有yn


wc又是什么？
C=3,类别数3，c=yn，c是某个标签索引，
wc就是yn标签对应的数据x的第c个索引位置上数据的权重，
该数据值与标签one hot编码中唯一的1对应，
损失函数会让这个模型值不断逼近这个1,

对于模型输出,加入批次维度，此时这个值被描述为
x[批次n][类别c]

ignore_index

 
ignore_index (int, optional): Specifies a target value that is ignored
    and does not contribute to the input gradient. 
    When
    :attr:`size_average` is ``True``, the loss is averaged over
    non-ignored targets.

ignore_index,被忽略的且不参数梯度计算的索引 

NLLLoss使用举例

请看举例

 
import torch
# 模型输出，预测值，特征与标签类别同
predict = torch.Tensor([[0.1, 0.1, 0.1],
                        [-1.2, -0.2, 0.2]])
# 标签，真实值
target = torch.tensor([0, 2])  # C=3 

result = 0
for i, j in enumerate(range(2)):
    tmp = predict[i][target[j]]
    print(i,j,"tmp:",tmp)
    result -= tmp
    print(i,j,result)
print("res:",result / target.shape[0])

loss = torch.nn.NLLLoss()
print("res:",loss(predict, target))

0 0 tmp: tensor(0.1000)
0 0 tensor(-0.1000)
1 1 tmp: tensor(0.2000)
1 1 tensor(-0.3000)
res: tensor(-0.1500)
res: tensor(-0.1500)

NLLLoss灵活运用

关键点

 
模型输出变量的单调递减函数 

NLLLoss将复杂的交叉熵计算简化为了y=-x 

好像是没得优化了，因为y=-x已经够简明了 

但仍有变通的余地，下面看看NLLLose在序列到序列中的应用 

 
def maskNLLLoss(inp, target, mask):
"""
功能描述
    - 计算模型预测单词与target标签单词之间距离
    
输入参数
    - inp: 某个位置一个批次的单词
    - inp.shape=[64, 7826] = [batch_size,dict_len]
    - target: 对应答句相应位置单词的索引
    - mask: 该位置是单词还是pad 
输出参数
    - 批次平均损失
    - 批次中单词个数

--------------
按位置计算，一次计算某个位置上一个批次的单词；
不同的句子长度不一致，所有句子在批次处理时长度皆为MAX_LENGTH
mask记录对应位置是否为单词，是单词为True,PAD为False
比如某句子长度为8，那么这句话9这个位置上就是PAD，
9这个位置对应的mask为False
"""
# 某个位置一个批次有多少个单词
nTotal = mask.sum() # 表示一个批次的某个位置上有多少个单词

print(f"target.shape={target.shape}")  # target.shape=torch.Size([64])
index = target.view(-1, 1)  # [64, 1]


# 取与 标签对应索引位置 上的模型输出的 数据，其他的都不要了
# 比如某个单词在原dict_len=7826这个字典的索引为100，那么其他位置上的值都不是该单词
# output的最后一维与dict_len=7826这个字典索引对应
# 所以，若标签这个位置应该被预测为索引100对应的单词时，
# 那么output索引100对应的数值应该概率最大
# 针对每个单词，先获取标签单词在字典中的索引下标，从one-hot的角度看，只有该位置为1，其他位置皆为0
# 同样取出模型输出的单词维度对应索引下标上的数据，该数据将与1通过损失函数进行校正
# 让模型输出的单词维度相同索引下标的数据不断接近1，让损失慢慢减少
# inp[batch_size,dict_len]单词维度dict_len做了softmax，其和为1
# 当某个索引位置上的数据接近1时，其他位置将趋于0
y = torch.gather(inp, 1, index)  # [64,1]
y = y.squeeze(1)  # [64] 

# 交叉熵计算，计算一个批次的两个分布之间的距离，模型预测的单词与标签单词的距离
# -(lable*log(y) + (1-lable)*log(1-y))
# lable = 1 , -log(y)
# crossEntropy = -torch.log(torch.gather(inp, 1, index).squeeze(1))
crossEntropy = -torch.log(y)  # [64]

# 取有单词的位置上的数据，不计算PAD
loss = crossEntropy.masked_select(mask).mean()
loss = loss.to(device)
return loss, nTotal.item()

 
整个代码段都是为下面这一行服务的 
crossEntropy = -torch.log(y)

个人感觉这个函数更符合 负对数似然损失 这个名称，毕竟这里面有负对数

同时，这段代码也告诉我们，工作实践中的代码，要比学习阶段的练习代码 复杂一些

torch.gather(inp, 1, index)

 
input.shape = [64, 字典长度]，这也是模型的输出，
并且已经做过softmax了，就是已经转概率了

dim=1 就是 维数为字典长度 的向量 这个维度 
index对应这个向量的索引下标 

利用 torch.gather 直接从模型的输出中 取出标签对应索引位置上的数据y
其他的都不要了，
然后将y代入简化后的交叉熵计算公式，就是这个 负对数似然损失函数 
就得到了模型输出与标签两个分布之间的偏差 

one hot的1

体会one hot的 唯 1 性

 
1这个数，太神奇了，此处借这个场景，要说的是这个设计思想的中的 唯1性 这一点 

一个向量表示一个事物，比如，大象，常态思维会这样表示：
[年龄，身高，体重，鼻子形态，腿形态...] 

而one hot的思想并不是这样的，
它强调一个向量中 有且仅有 一个值是重要的
并且这个值就是1,
这1就是个整体，完全代表了该事物，
不再对这个1进行拆分，拆分出年龄，身高，体重等等更细的维度 

 
一个事物就是一个1,就是一个完全体/完整体 
事物与事物之间的差异，并不在于大小，而是在于位置 
位置的差异，由索引位置，也就是不同的维度体现，
不同的事物在 不同的维度上 
每个事物都是1 
两个事物在一个维度上，那是量的差异；在不同维度上，那是质的差异 

 
同时，这个1也是概率的1,
这个让其他位置都是0,这导致整个向量的 模/长度/距离 也是1,
向量的模为1,意味着向量之间的差异完全由其夹角体现，
而one hot向量与向量之间全是正交，即垂直相交，
任何一个向量与其他向量之间都是垂直相交，
正交意味着，本维度在任何其他维度上的分量是0,
换成人话说是，该事物与其他事物没有半毛钱关系... 

这都快达到坐标系的标准正交基的层次了... 
坐标系的基可用于表示向量空间内的任何向量，
是一个 基本 或者说 最合适的最小表示单位了
没有比标准正交基更适合来表示一个空间的向量了 

话说回来，这么好，为啥数据不这么表示呢？
因为这样做向量太长了，长到计算机算不动，无法落地实现... 
所以，one hot标签适合类别不多的分类问题

参考