范数 norm

L1范数：1维上的距离

 
各个元素绝对值的和

|a-b|，两个数相减，再求绝对值，再相加，是常见的距离的计算方式
也叫L1范数

L2范数：多维上的距离

 
各个元素的平方和再开平方

两个向量
A=(a1,a2,...,an)
B=(b1,b2,...,bn)
设xi=ai - bi,那么向量AB的距离可表示为 

 
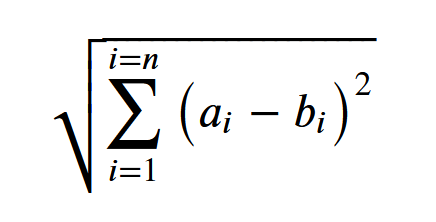
这就是L2范数，也是欧氏距离，表示多维上的距离/差异 

L2范数将距离的概念 扩展/加强 了

向量有多维，就像花有绿肥红瘦一样，不同事物之间的差异是多方向/方面/维度的，

各个维度的差异积累起来的总差异，也是两个事物之间的差异，

这种差异在数学上叫 L2 norm 

L1 Loss

L1 Loss:绝对值损失,再对绝对值求均值

 
nn.L1Loss(size_average=None, reduce=None, reduction: str = 'mean') -> None

Creates a criterion that measures the meanL1 Loss 示例 absolute error (MAE) between each element in

the input :math:`x` and target :math:`y`.

size_average, reduce 这两个参数已废弃，看 reduction: str = 'mean'

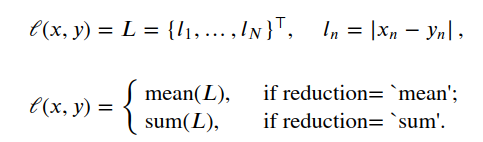
L1 Loss 示例

L1 Loss 示例

  
where :math:`N` is the batch size

import torch
from torch import nn 

loss = nn.L1Loss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)
output = loss(input, target)
output.backward()

output
tensor(1.1354, grad_fn=MeanBackward0)

SmoothL1Loss

Smooth L1 Loss为L1 Loss的平滑处理

 
Init signature:
nn.SmoothL1Loss(
    size_average=None,
    reduce=None,
    reduction: str = 'mean',
    beta: float = 1.0,
) -> None
Docstring:     
Creates a criterion that uses a squared term if the absolute
element-wise error falls below beta and an L1 term otherwise.
It is less sensitive to outliers than :class:`torch.nn.MSELoss` and in some cases
prevents exploding gradients (e.g. see the paper `Fast R-CNN`_ by Ross Girshick).


For a batch of size :math:`N`, the unreduced loss can be described as:

 
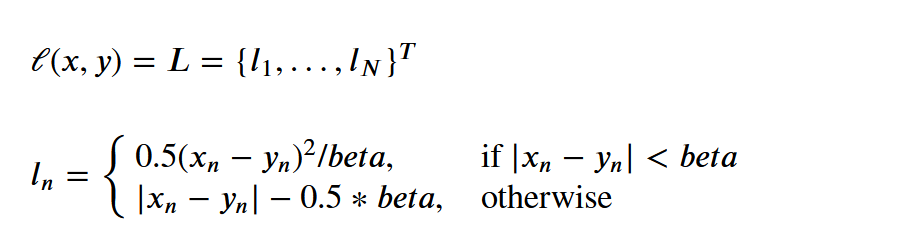
.. note::
Smooth L1 loss can be seen as exactly :class:`L1Loss`, but with the :math:`|x - y| < beta`
portion replaced with a quadratic function such that its slope is 1 at :math:`|x - y| = beta`.
The quadratic segment smooths the L1 loss near :math:`|x - y| = 0`.

当x与y相异不大时， 使用的是平方，只不过加了个参数，是扩大还是缩小分布的差异，看参数设置， 
相比MESLoss，可以防止爆炸，数据偏差大时，不再使用平方了，而是回到绝对值（即L1Loss），
只不过又减了一个数,并且这个数是正数，意思就是让偏差小一点
不管怎样，这两者都会随着偏差的增大而增大，能够反应分布之间的差异

L1 Loss易受异常点影响，且绝对值的梯度计算在0点容易丢失梯度。
Smooth L1 Loss 在0点附近是强凸，结合了平方损失和绝对值损失的优点。

L2 Loss/MSELoss

 
nn.MSELoss(size_average=None, reduce=None, reduction: str = 'mean') -> None
  
Creates a criterion that measures the mean squared error (squared L2 norm) 
between each element in the input :math:`x` and target :math:`y`.

 
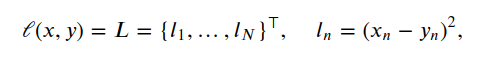
where :math:`N` is the batch size. 
If :attr:`reduction` is not ``'none'`` (default ``'mean'``), then:

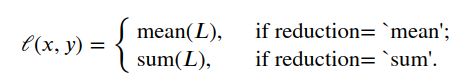
Shape

 
- Input: :math:`(*)`, where :math:`*` means any number of dimensions.
- Target: :math:`(*)`, same shape as the input.

MSELoss要求模型输出与标签的shape一致，
并不像交叉熵那样，标签支持索引的格式
也没什么，就是遇到MSE加一个标签与模型输出的shape是否一致的判断就可以了 

MSELoss示例

 
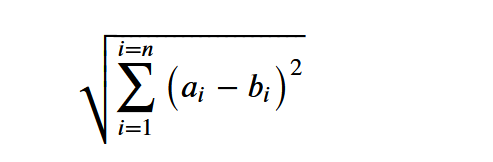
$\displaystyle \sqrt{ \sum_{i=1}^{i=n}{ \big(a_i-b_i\big)^2}}$

示例

 
import torch
from torch import nn 

loss = nn.MSELoss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)
output = loss(input, target)
output.backward()

output
tensor(1.0446, grad_fn=MseLossBackward0)

参考

    L2范数的理解
    什么是范数（norm）？以及L1,L2范数的简单介绍
    拉普拉斯分布