全遍历计算

完全不管函数是个啥，直接全定义域上生成间隔较小的一组随机数，然后求结果的最小值
- 容易实现
- 定义域广的话，需要生成的随机数量大
- 因为是随机数，所以结果有些不稳定
- 数据量大时，效率低，完全是暴力计算

蒙特卡罗算法（Monte Carlo Algorithm）是一类利用随机数进行数值计算的方法，特别适用于解决复杂且难以通过常规方法直接求解的问题。其中，使用蒙特卡罗算法寻找函数的最小值是一个典型的应用。这种方法通过大量随机采样和统计分析来逼近目标函数的最小值。
基本步骤

定义目标函数：
首先，你需要有一个待优化的目标函数 f(x)，其中 x 通常是多维的向量。

生成随机样本：
在目标函数的定义域内生成大量的随机样本点。例如，如果 x 是一个二维向量，可以在 [x_1_{\min}, x_1_{\max}] \times [x_2_{\min}, x_2_{\max}] 的范围内生成随机点。

计算函数值：
对每个随机样本点计算目标函数的值。

记录最小值：
记录迄今为止遇到的最小函数值及其对应的样本点。

重复采样：
根据需要重复步骤2到步骤4，增加样本数量以提高估计的准确性。

输出结果：
在达到预定的样本数量或满足其他停止条件后，输出记录的最小值及其对应的样本点作为估计结果。

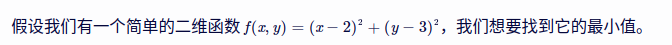
import numpy as np

# 定义目标函数
def f(x, y):
    return (x - 2)**2 + (y - 3)**2

# 设定定义域
x_min, x_max = -10, 10
y_min, y_max = -10, 10

# 生成随机样本
num_samples = 100000
x_samples = np.random.uniform(x_min, x_max, num_samples)
y_samples = np.random.uniform(y_min, y_max, num_samples)

# 计算函数值
values = f(x_samples, y_samples)

# 记录最小值
min_value = np.min(values)
min_index = np.argmin(values)
min_x, min_y = x_samples[min_index], y_samples[min_index]

print(f"Estimated minimum value: {min_value}")
print(f"Corresponding point: ({min_x}, {min_y})")

函数是有单调性，在一定范围内，会单调递增/递减

随机选一个起点，向前一小步，
- 如果函数值变大，就回退一点点
- 如果函数值变小，就前进一点点

def f23(x1,x2):
    y = (x1-2)**2 + (x2-3) **2
    return y

比如上面这个函数，有两个变量，在AI中默认两个变量相互独立，
虽然肉眼可见是x1=2,x2=3时可取得最小值，
但如何找到一个方法，让计算机对于任意函数都能求出最小值？

第一步，如何使用上面的方法，计算多变量函数的最小值？

A:一个变量还好说，现在有多个变量？

B:你说什么？

A:现在有多个变量

B:不是这一句，是上一句

A:一个变量还好说

B:对，就是这一句，既然当函数只有一个变量时，单调性变化少，那么就一个一个变量地观察；先解决一个再说下一个

def fn(x):
    return (x-2) ** 2

再回顾一下蒙特卡罗方法：全遍历比较

x = np.random.uniform(low=-100, high=100, size=10000)

def fn(x):
    return (x-2) ** 2


# 起点
x_min = x[0]

# 假定第一个就是最小值，若有值比它小，则将更小的值赋予它
y_min = fn(x_min)

for ele in x:
    y = fn(ele)
    if y < y_min:
        y_min = y
        x0 = ele

print(x0, y_min)  # 2.016519470488859 0.00027289290523228854

微调方法

#随机选择一个起点
x0 = np.random.uniform(low=-100, high=100, size=1)

print(x0)

delta = 0.01  #微调大小

for _ in range(10000): #尝试1万次
    if fn(x0 + delta) < fn(x0):  #前进一点点
        x0 += delta              #变小了
    elif fn(x0 + delta) > fn(x0):
        x0 -= delta              #变大小
    else:
        print("OK!!!")
        break

print(x0, fn(x0))

[81.24773959]
[1.98773959] [0.00015032]

结果说明当x=1.98773959时，fn取得最小值0.00015032

同样的方法解决另外一个变量

def fn(x):
    return (x-3) ** 2


#随机选择一个起点
x0 = np.random.uniform(low=-100, high=100, size=1)

print(x0)

delta = 0.01  #微调大小

for _ in range(10000): #尝试1万次
    if fn(x0 + delta) < fn(x0):  #前进一点点
        x0 += delta              #变小了
    elif fn(x0 + delta) > fn(x0):
        x0 -= delta              #变大小
    else:
        print("完美!!!")
        break

print(x0, fn(x0))

[-86.72279204]
[2.99720796] [7.79549379e-06]

算法说，起步并不重要，只要你不断学习，不断前进，就会有进步！

这个函数可以看作是两个变量的的函数的和，那如果是差呢？

将这看作一个新的问题

如果单变量的函数值都变得很小，至少从现在的结果来看，不管是和还是差，最终的函数值也会很小
- 其实这里是想让一个函数趋于0，所以使用正的函数举例
- 如果是负的，让其绝对值趋于0即可

该方法的问题，实际上只能求极小值
局部最优

很可能有个地方有个最小值就在那来回摆动，不再尝试了，
至于其他地方有没有更小的值，该方法就无能为力了

如果有一种方法能取得 单个变量函数 的变化趋势 就好了

就是知道单个变量函数在一定范围内，是增还是减，

在数学上，导数可以解决这个问题
- 函数增，对应区域的导数为 正
- 函数减，对应区域的导数为 负
- 不管函数再复杂，只要它可导，就有此规律

导数的正负

y=fn(x)在x处的导函数值记为dx

x = x - 步长*dx
- 当函数增加时，dx为正，x变小, y变小
- 当函数减小时，dx为负，x变大，y变小

该公式可以保证x总体，在大趋势上，大方向上，是朝着y的最小值处前进的

导数的大小

步长，
- 如果起点离最小值点的距离大的时候，步长大一些，可以加速
- 如果快到最小值点附近了，那么步长小一点，会更准一些

导数可以解决这个问题吗？
- 有些函数在极值附近变化缓慢，导数值就小，这样就可以
- 可现实是，这个函数正是要求的，不知道的，或者说函数是复杂的，
- 所以导数解决不了这个问题

该问题在深度学习中，由优化器解决，
- 在训练开始时，步长大一些
- 之后，步长小一些