五张卡片，共有 3个A，4个B
每张卡片最多一个A，最多一个B

P(A)发生的概率 = A的卡片数/总卡片数 = 3/5
P(B)发生的概率 = B的卡片数/总卡片数 = 4/5
P(AB)发生的概率 = AB卡片数/总卡片数 = 2/5

P(B|A)  = 包含A的卡片中B的卡片数/A的卡片数 = 2/3

P(B|A) A发生的条件下B发生的概率

这里面最重要的是，也从来不说出来的是，全集：五张卡片

全集，划定了范围，但在讨论问题，分析问题的时候，从来不提，
没有这个前提，一切讨论便没有意义，为什么不提？
因为如果每次都提这个，写字累，打字也累，说话也累，大家知道就好了，
嗯，默认大家都知道，大家平时说话也不是这样的吗？省略了很多大背景...

什么时候会出问题？出现交流障碍？
就是新手来的时候，新手不知道你那些没有说，但很重要的大前提，
就自然地不太理解你在这之上所说的东西了

P(B|A)  = P(AB)/P(A)

P(A|B)  = P(AB)/P(B)

看这公式多简洁，新手 看不明白 才是正常...

P(B|A)P(A) = P(AB) = P(A|B)P(B)

P(B|A) = P(A|B)P(B) / P(A)

P(B|A) = P(A|B)P(A) / P(A)

P(y|x) = P(x|y)P(y) / P(x)

一个样本x是y的概率 = 标签y中样本x的概率*标签y的概率 / 样本x的概率

分类与标签

通常使用标签描述分类
二分类：y1 = [1,0],y2=[0,1]
三分类：y1 = [1,0,0],第1个位置上的1表示该向量属于某个类型/分类

对于二分类问题，
一个样本xi 属于y1的概率为P(y1|xi),属于y2的概率为P(y2|xi)

属于 哪些/哪个 类别的概率高，该样本是 哪些/哪个 类别的可能性就大
默认做法是最概率最大的那个类别

P(yi),P(xi)的计算就是 数 数，就是统计
P(xi/y1)就是标签为y1的样本中，xi出现的概率

工程近似

AI工程 中 P(yi/x)表示输入一个样本x输出某个标签yi的概率

P(yi|x) = P(x|yi)P(yi) / P(x)
i 属于[0,1,2,...,n]

对于任何一个yi来说，P(x)是共用的，
同时该公式只需要 比较出哪个标签的概率最大即可，

所以该公式可使用下面的公式近似
P(yi|x) = P(x|yi)P(yi)

概率是描述一件事发生可能性大小的规律
是由事件本身所决定的，固定的性质，

比如，
一个硬币只有两面，那么抛下后，任何一面出现的概率是1/2
一个筛子有6面，抛下后，任何一面出现的概率是1/6

这与是否有人去做实验没有关系，即在做实验之前就是确定这个事件的概率
这是就先验概率，先于实验就确定的概率

自然界事件是多以正态分布呈现的，
不像硬币1：1的正反出现，也不会像筛子一样，每面出现的概率都是一样的
即，事物的性质决定了其中事件的概率不是均匀分布的

一个集合中，比如，年收入，
有极少数年收入是 +百亿的，也有极少数人年收入是 -百亿的，就是一年赔了几百亿

比如，身高，大部分人身高差不多，集中在1.5-1.8米之间，
但人活几十年也能见到一两个需要你抬头才能看到人家脸的高个

这是单维度的事件，有些场景中是多维度的，有很多的事件，
多到根本不知道有哪些事件，
比反洗钱，反欺诈场景，你想去收集所有的欺诈手段，这不可能的
只能收集已经出现的，并且是经常出现的手法，才能被收集到

这就错过了一些样本类型 ，错过的多了就会影响样本的质量
样本是用于代表客观世界的现象的，很多样本收集不到，这个代表力就不足

针对这些问题，处理的方法有两类：
平滑处理：高斯平滑，拉普拉斯平滑,加一个很小的数，n/N转为(n+1)/(N+1)等

忽略不计：比如求最大概率，
目的是求最大概率时，那些小概率事件本来就是要忽略不计的，
求众多可能中最大的那个可能，本身就是要排除/过滤掉小概率事件的，
有没有收集到一些小概率的事件关不影响求最大的那个概率
注意，这里说的是忽略，不计算了，不管了，没说让那些小概率事件为0

理论与工程

还是一种情况是，面对数据的缺失，事情没做好，

没做好就没做好吧，但不是最差的那个就行了，就是跑赢同行/对手就可以了

在工程上，计算概率时，
哪怕事件发生的概率再小，或者没有，
也不直接设置为0，而是设置为一个很小的数

比如，抛硬币这件事，简单，
比如，猜一猜，抛下一枚硬币，出现正面的可能是多少，我大概也会猜是 1/2 ，不算难
很多事情，到这里就结束，止于讨论...

这件事情的发展只停留在了思考的层面，一些大人物提倡要动脑思考，要多思考，
于是很多人去思考了,不断思考，经常思考，累了就休息，有精力了就读书，就思考...
N多年后终有所得，于是立书留于后人思考...后人不借鉴于前人，重蹈覆辙...轮回成...

但有人去实践操作了，把一攻硬币抛了上万遍，不断地记录，去验证，再记录，再验证...
这就很难了，非常地艰难/困难，做成就很不容易了，
做成之后，能推广开来，让大家接受这种方法，就更不容易了，
但如果做成了，其影响力将是无比巨大的，巨大到可能诞生出一个文明分支-科技文明...

到这一步，并没有完...
这件事虽然难，哪怕我笨一点，但我知道它的重要性，我坚持去做，我也能做到...
但抛硬币这件事，不管抛多少遍，它只是接近1/2，但永远不会真的就等于1/2

是不断接近，但却不会相等！

于是极限思想就诞生了
不诞生也没办法啊，那么多人做了那么多实验，但就是无法转化为数学上的 绝对相等，
不转化为数学上的绝对相对，就无法以此为基石，推衍下一阶段...

可以想象一下，在数学的公式世界中，公式的两边都是绝对等价的，
通常一边是我们理解的，另外一边是我们不太理解的，要通过这个 绝对的等号“=”把两边连接起来
如此，无数个公式连接起来，形成一张大网，就是数学对这个世界的描述，精准无比

现在来一个约等，虽然很近似，你内心也无比肯定抛一枚硬币出现一面的概率就是 1/2
在感性的交流中，你可以无比笃定的说，绝对是1/2,绝对是1/2,绝对是1/2
但在数学的世界中，不认！容不下一丝一毫的差异！

于是极限思想就诞生了，同样用绝对相等的公式推导出其极限，使之可以普遍运用，
这样终于可以在数学上说，抛一枚硬币出现一面的概率就是 1/2 了

在极限方法诞生之前，对很多的事物解释皆处于 “道可道，非常道”的层面

大概知道一个规律的样子，在不断接近它，但却描述不清楚它，
时间，空间，环境，人的不同，对它的描述也有差异

极限方法诞生之后，就产生了一种对于某种规律的 精准描述，
从此之后，就开启了认知世界的一扇新的大门

从此，便是 “道，可道...”
认知清楚的规律，不会因为 时间，空间，环境，人的不同，而产生任何差异

理解朴素贝叶斯分类的拉普拉斯平滑

https://zhuanlan.zhihu.com/p/26329951

高斯平滑

https://baike.baidu.com/item/%E9%AB%98%E6%96%AF%E6%A8%A1%E7%B3%8A/10885810?fr=ge_ala

高斯模糊（英语：Gaussian Blur），也叫高斯平滑，通常用它来减少图像噪声以及降低细节层次。

其视觉效果就像是经过一个毛玻璃在观察图像，
从数学的角度来看，图像的高斯模糊过程就是图像与正态分布做卷积。

频率的平滑处理

条件概率计算，要去求概率，概率就是 数 数，就是统计
在具体的实验中，其实求的是频率，以频率作为概率的近似

AI工程 中 P(yi/x)表示输入一个样本x输出某个标签yi的概率

P(yi|x) = P(x|yi)P(yi) / P(x)
i 属于[0,1,2,...,n]

举个特殊的例子，
随机说一句话，不限语言，判断这句话是积极还是消失

假设全球几百种语言总共有1000万个常用句子
可以有重复，重复越多的句子表示说的越普遍，
比如，“不知道”这三个字就会大量出现在各种语言中
全体句子集合为S，其个数N=1000W

你所说的话，有可能在这N个句子中，也有可能不在
如果不在，则概率P = 0
如果在，设其出现的次数为 n ，则其概率P = n / N

客观上讲，人类所说过的话绝对不止这N=1000W句，因为这里面不限重
你要是专门说一句没有人能听懂的话，很可能就不在这里面了，那其概率就为0

在工程为了避免这种情况，进行以下平滑处理

P = n / N  约等于 (n+1)/(N+1)

如果n很小，比如为0,那么(n+1)=1,1/(10000000+1)在计算机中约等于0,或者说就是0
- 比如收集1000W句各国语言的话已经不容易了，再扩展数据集，可能电脑算不动了...就算电脑算的动，人也收集不动了...
- 全体应该代表所有句子的集合，实际上只有常见的那一部分... 人力有时尽...
- 所以，你随便说一句，尤其是故意的情况下，可能真不在这个集合中
- 这也是算法界的一大现实，不缺少理论上的算法，缺少验证算法的数据！

如果n很大，比如1W，那么 n / N  还是约等于 (n+1)/(N+1)

实际上，在N是一个比较大的数值的前提下，n取什么值关系就不大了...
+1就是为了不让它为0，达到这个效果就可以了

在标准差的计算中， (x-mean)/(std+1e-7)
在分母中+上一个比1e-6还小的数，防止std为0导致计算机抛出异常，
因为加的数很小，在计算机中近似于0,所以不影响原有的计算
也是一种平滑处理

为什么宁可小也要避免0呢？

一种场景是像求标准差这种，在分母上，若为0则抛出异常

还有一种是联乘的场景
比如P(开心 就好)=P(开心)P(就好)，这是一个联乘，
如果P(开心)的概率为0,那么整个句子的概率为0了，
这会导致后面的单词不管出现的概率有多大，其结果都是0，再无回归的可能了

最重要的是模拟现实，
现实中很少有概率为0的事情,就是绝对不可能发生的事情
笛卡尔的一个观点是，一切皆有可能，一切都可以怀疑这件事不需要怀疑，
你甚至可以怀疑自己是不是虚拟的...

一切皆有可能，希望最美，哪怕发生的概率很小很小...
AI就是在模拟现实，因此时计算是会进行平滑处理，避免0的出现

比如，概率密度图描述事件概率的分布，是一个中间高两边低的图形，
两个边无限接近x轴，却永远也不会真的与x轴相遇！

数学很严谨，在讨论一个问题之前，会先设定一个讨论的范围，
就是一个集合，一个全体
这样出错，出现误解，出现不确定因素的可能就降低了很多

AI从数据中学习规律，然而很多场景下数据是收集不全的，凑不齐这个全体/全集

在理论上，可以做假设，可以玩虚的，可以进行纯逻辑上的推导

做工程时，面对残缺的数据，如何去解决问题，如何去落地产生价值？
这时有两个方向
- 一个是追求规律本身，去想办法掌握更多，更全的规律，去拿更多的数据
- 超越竞争对手即可，自身效果很差，但在同行中不垫底，不是最后一名，就可以有口饭吃

分析数据，收集特征，收集的是不同维度的特征，
相同维度的特征，即重复的特征，要一个就可以了，多了也没有正向作用

理论上相互独立，不重不漏的特征是最完美的

但工程上，特征通常会有些重复

此时，会使用一些设定，去简化计算，
比如，直接假定所有特征是相互独立的，不去管它们是否真的相互独立
如此，P(AB) = P(A)P(B)

特别是在NLP领域中
P(y1|x) 近似于 P(x|y1)P(y1),x是一个句子，由单词序列组成
如果单词出现的概率相互独立，那么就有
P(x|y1) = P(x1|y1)P(x2|y1)...P(xn|y1)
条件相互独立，在y1的条件下,句子中各个单词相互独立的概率

这如极大地简化了计算过程，并且减少了联乘的次数，使得工程能够继续做下去了...

非NLP领域，比如机器学习中，
数据预处理阶段也会做一些共线性分析，将重复度高的特征去掉
这样进入模型的数据，至少没有线性重复的

去重操作，也是有理论支撑的

效果呢？
就是本来不是相互独立或者不知道是不是相互独立的，就假设为相互独立，影响效果吗？

影响，但在此情况下的工程 也 能用！

另外，在收集特征时，也需要注意，明显重复的特征，就不要收集了

朴素，指简易，不麻烦，不复杂，
就是简单地认为 特征之间是相互独立的，那么就有

P(x|y1) = P(x1|y1)P(x2|y1)...P(xn|y1)

条件相互独立，在y1的条件下,句子中各个单词相互独立的概率

分步乘法计数原理

如果事件A与事件B相互独立，相互之间无影响，那么有

P(AB) = P(A)P(B)

概率 就是 统计，就是数 数 ，就是计数
简单的计数，直接数就可以，复杂的计数要使用 排列/组合

举例：
事件A表示 一个员工过去10天中考勤异常的天数
事件B表示 该员工过去10天午餐吃的面食的天数

相互独立
事件A与事件B是相互独立的，
这里指出了两个事件是不是相互独立，主要取决于业务，取决于事件本身的性质

一个员工中午吃不吃面食，跟他当天考勤是否异常没有直接联系

事件A与B
这里只考虑事件A与事件B，其他的 都叫 其他类别，即不是A或B
考勤只有正常异常两类，没得说
吃饭，除了吃面，还有很多情况，这里只归于是不是面，是就代表事件B发生，不是就代表B不发生

比如抛硬币只有正反，没得说
掷色子是有6个点，如果只考虑2是否出现的话，
不是2的事件就不是事件2，也可以将不是2定义为事件B

回归正题，经统计发现一个员工过去10天中，考勤异常2次，中午吃面5次
求该员工过去10天中，中午吃面且考勤异常的概率

这是一个组合的问题，这两者是同时发生的，没有顺序关系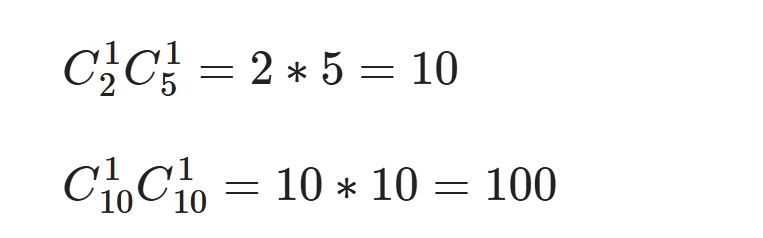

10/100 = 10%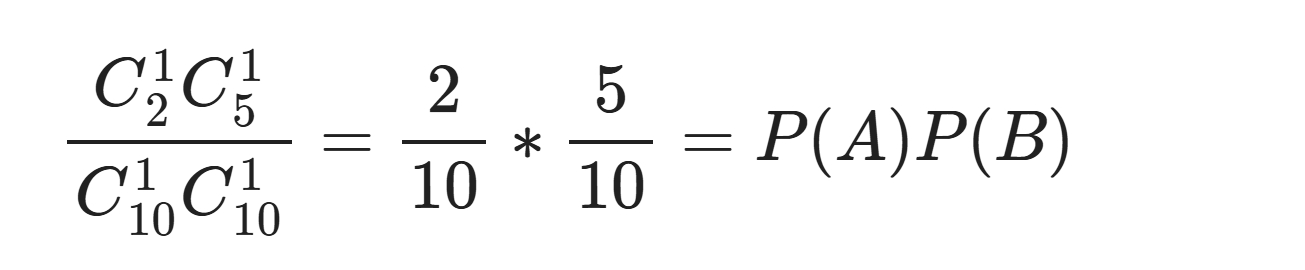

这里从排列组合的角度解释了，为什么当两个事件相互独立时

两个事件同时发生的概率 = 两个事件单独发生的概率之积

离散必有间，连续可有间可无间

首先讨论离散，数数，
数一数你走过的一段路旁边有几棵树，按类别计数，如此可求某个类别的概率
这就是离散数据

那如果是一条河中的水，一片沙漠中的沙呢？
给你一袋大米呢？数颗粒
给你一袋面粉呢？怎么数？

何为连续何为离散？

以为/感觉的连续真的是连续吗？
比如，
电脑屏幕的画面，感觉上是连接，实际上是一张张离散的图片播放的，只是眼睛无法区分

沙漠中的沙与天上的星星呢？
如果将沙漠中的沙说成连续的，感觉还不明显
按这个思路说天上的星星也是连续的，就明显感觉不合理

空间中物体的连续讨论

电脑屏幕连续吗？看着很平滑，实际上屏幕都是由一个个点组成的，m*n大小个像素点

有了元素周期表以及原子电子的理论之后，
如果从原子电子的角度看空间中的事物，所有物体都是镂空的，内部空间无比巨大，空旷
就跟站在地球上看银河系差不多，空旷才是主题...

这里讨论了，感觉，肉眼
还有纯理论，纯逻辑上的连续，
通常会认为数轴是连接，它与实数对应，
但实际上实数中是有无理数，无限不循环小数的，也就是说，单维的数轴也不连续

收一收，想法太多了，讨论的面太多，要收一下范围

通常所讨论的 连续与离散 是 宏观上，感觉上的连续，
只要出现人力有时尽的场景，
即对于人来说，有数不完的数，就是无限的，连续的，不过于追求它是不是真的连续

个体与个体之间有明显的距离，可以通过数数完成的，就是离散的

这就是统计学中的 连续与离散 ，皆是在宏观领域，不涉及微观

在逻辑的角度看连续，就是不间断，间断就不连续，
本人提出一个新的词来描述这个场景，“无间”

没有间隔就是连续，即无间
有间隔叫有间

比如，
时间应该是无间的，时间本是一个纯虚的，看待事物运动的一个维度，它应该是无间的
即时间静止是不存在的，事物在绝对0度下可以不运动，
但时间还在走，只是事物的状态不再变化了

整理一下，连续与离散，
- 生活中容易数个数的就是离散的，不容易数的就是连续的
- 看着，主要指眼睛，连在一起就是连续的，分散开来的就是离散的

比如，水流是连续的，面粉是连续的，光是连续的，声波是连续，事物的运动轨迹是连续...
从这个角度看去，这世界是连续的...

沙漠与星星的问题
- 沙漠中的沙子与沙子之间的距离很近，沙子在人所接触的事物范围内，它体积小，可以认为是连续的
- 星星体积大，巨大，超级大，但它们之间的距离/间隔 更大，比它们体积的亿万倍还大！离散性很明显
- 数不数的完是一个问题，它们之间的距离是另外一个问题
- 星星是离散的，沙漠中的沙子,有间，但是连续的，沙子太多了，连的太紧了，到处都是...

至此，可以说，这个世界是连续的

从计算机数据的角度看，
在电脑中看到的数据，都是离散的，
因为连续的数据是无限的，你看不完,计算机也存不下...

这就是我们看世界，是离散的！

既然都是离散，为什么还要区分哪些是连续，哪些是离散？

为了模拟现实，为了追求客观世界的规律

这是两大类别，

虽然看上去一样，
但如果知道这数据对应现实的事物是连续的，
比如，一些公式计算，有助于人们更好地理解客观世界

如果知道这数据对应的是离散的事物，
比如抛硬币，数小球，人口统计等，就能更好地理解这些数据

即，要明白数据背后客观世界中对应的事物是连续还是离散的

离散可有限可无限，连续必无限

从定性与定量的角度总结一下

定性分析，方向与范围 分为 生活与数学
在生活中，
由于肉眼的能力所限，能连在一起的，就是连续的；有明显距离的，就是离散的

在数学上，
连续的数据是可以有间隔的，有范围


定量分析，在个数上
离散数据的个数一定是有限的
连续数据的个数一定是无限的，无穷无尽的...

在数学上
离散数据是有限的，可列的，哪怕你数不过来
连续数据是无限的，

数学科学 是以 人能收集到的 有限的数据 代表 客观世界
- 当数据收集完后，连续与离散就没有区别了，都是 有限个数的 数据集
- 它们对应的 在客观世界中的事物 是不一样的，这才是离散与连续的本质区别
- 在工程落地时，它们都是数字，数字化...数字化 就是 将一切转化为数字...

在肉眼可见的层面上，离散与连续数据都是有限个数的，都是数字，没有区别
区别在于它们背后所代表的事物，所代表的规律

[0,1]范围内的数字是无限的
比如，有0.1,就可以有0.01,0.001,0.0001,...
这不同的于无限不循环小数，比如3.1415926...，这是同一个数后面有无限个小数位
连续的无限指不同数据个数上的无限，不是同一个数后面的小数个数

数学与工程落地

数学上，统计个数/次数 是一个离散型变量，一个，一次，没有半个，半次

工程上，是有半个，半次，比如n个客户最近1个月交易次数统计后，可以求均值，平均交易次数

概率密度图不是概率图，但它与单点概率同比变化，胜似概率

因为[0,1]范围内有无限个数，所以对于某一个确定的数，比如0.1出现的概率为0
因为分母的数字个数为无穷大 ，那如何求连续型数据的概率？

这一点涉及 大数定律与中心极限定理，
https://blog.csdn.net/qq_40765537/article/details/106740918?sharetype=blogdetail&sharerId=106740918&sharerefer=WAP&sharesource=

以及 微积分相关的知识

微分，工程近似

x轴上取一点x,单点x的概率为0
概率密度图中的面积是概率
    取x(对应y值为a)附近一个微小的距离b，那么b就是一个长度，a*b就是x附近小矩形的面积，
    以此近似表示点x的概率

点x处的概率与点x处的概率导数同比

前提：连续变量，无穷无尽的数据...
    (可以认为 任意两个 相邻数据 之间的距离是无限小，这个仅是辅助理解的个人观点，本人没证明过...)

导数是两个变量 变化的 比率(大概这么说，通俗地说，非严格数学定义，仅是本人心中的想法...大概这意思)
就是一个变量相对另外一个变量 变化的快慢程度
- y=2x,不管你x怎么变化，我y永远是你的2倍！

概率密度图不是概率图，但任意一个点的概率与该点在概率密度图上的y值，同比
- p(x) = a*b，b对于所有矩形是相同的，尽管b很小
- 因此p(x)主要取决于a，a大p(x)就大,a小p(x)就小

贝叶斯

P(B|A) = P(A|B)P(B) / P(A)

P(y|x) = P(x|y)P(y) / P(x)

一个样本x是y的概率 = 标签y中样本x的概率*标签y的概率 / 样本x的概率

假定特征相互独立

朴素，指简易，不麻烦，不复杂，
就是简单地认为 特征之间是相互独立的，那么就有

P(x|y1) = P(x1|y1)P(x2|y1)...P(xn|y1)

条件相互独立，在y1的条件下,句子中各个单词相互独立的概率

工程近似：连续概率等比替换

对于一个给定的样本x，那么该样本出现的概率是固定的，是一个常数
P(y|x) = P(x|y)P(y) / P(x) 等比于 P(x|y)P(y)

假定特征相互独立后
P(y1|x) = P(y1) P(x1|y1)P(x2|y1)...P(xn|y1)

若x1是连续的，可通过与概率等比的概率密度图替代

离散变量

若x1是离散的，可通过数数计算离散概率
- 离散变量存在这样一种情况，测试集中会出现训练集中没有的类型
- 有可能是代码bug，也有可能是训练集没有收集全所有的类型，现实世界中是有的
- 这时，该类型出现时，给它一个极低的概率，比如1e-6

在概率密度图上并没有概率导数为0的地方，越远离中心，概率变化越缓慢，但还是在变化...
- 再进一步说，还是因为这世界是连续的
- 一些离散变量本就是从连续中采样出来的，比如，信号处理，语音等
- 对于一些本身离散的量，
  - 比如物体识别，一个苹果的大小等，在一定的范围内，也接近是连续的
  - 因为这世界有太多的苹果，尺寸就集中在那么一段长度上，导致虽然离散，却近似于无限个数
  - 一旦近似于无限，用连续型变量的计算方法来替代也是可以的
  - 但对于NLP文本处理的问题上，单词的数量虽然也多，但远远达不到接近无限的程度，
  - 常见单词也就几十万，对于汉字，常用汉字也就3000多，还得通过数数计算概率
所以对于离散型变量，
  - 有些变量可看作连续型的，比如那些本身就是从连续值中采样而来的
  - 而有些数据规模不大的类型，还得通过数数算概率，比如文本处理

选择可能性最大的

假定特征相互独立后
P(y1|x) = P(y1) P(x1|y1)P(x2|y1)...P(xn|y1)

如此，一个样本为某个标签的概率，转化为一系列概率的连乘

对于二分类问题，至少有两个标签，y1,y2
最终，选出概率最大的标签,作为该样本最终的归类

从三个维度描述自然界中的连续与离散

宏观世界
- 宏观
  - 贝叶斯的概率是指统计中的概率，统计就是数数，主要用肉眼看世界
  - 即这里不讨论微观世界，范围定为世界中肉眼所见的宏观层面的事物
- 世界
  - 这里实指巨大的数据量，
  - 虽说人力提取的事物是有限的，但其实对应着世界中的一些类别，
  - 默认所采样的数据能代表世界中对应的类别
  - 比如，一个果园的苹果，其实是默认这世界上所有的苹果跟这个果园中的苹果差不多
  - 至少其他果园的苹果与该果园的苹果的差别，没有苹果与 西瓜或香蕉 的差别大
  - 类别与类别之间的差异，是基于"世界/自然界 量级"这个巨大无比的数据量的，
  - 这个巨大的数据量通常以基本常识的形式呈现，默认大家都知道，所以讨论时通常不提及...


哲学中的主要矛盾与次要矛盾
- 比如说一个苹果坏了，是指这个苹果上有坏的部分，
- 也可能只是坏了一小部分，还有一大部分是好的
- 但对这个苹果的定性是，这是一个坏苹果
- 连续的事物可以通过 分段，滑窗，分桶，使之化为离散数据，
- 比如从窗户中看天，照片中看风景...
- 一如你的眼睛所见的世界，是一个个连续事物的切片...抬头看天，走路看地
- 离散的数据中也有连续的维度，比如，花草树木，一棵树从小至大这个过程是连续的


哲学中事物的共性与特征
- 万物有共性，这是说的世界本质是连续的，基于相同的事物发展演化而来
- 万物有特性，事物经过漫长的运动之后，
- 物以类聚，本来混沌一片的世界，变得 天是天，地是地，山是山，水是水
- 天是连续的，星球是离散的，水是连续的，水中的鱼是离散的...变得你中有我，我中有你

所以，
连续还是离散，都是有范围的，有条件的，确定讨论的范围与条件是很必要的

工程落地

贝叶斯在落地时，概率计算全部采用 连续型变量的概率计算方法，
即默认所有离散变量是连续变量的一部分

异常类问题
- 工程实现参考理论，依据理论，但也会考虑现实问题
- 现实中各种偏离理论的异常，比如年龄输入了一具很大的数，或者负值...
- 年龄有负值吗？
  - 理论中是没有的，实现中用户不小心/故意 输入一个负值，你能奈何？
  - 如果按连续的思维逻辑，就是那个概率密度图，
  - 那条导数曲线不断在接近x轴却永远不会真的相遇，
  - 一切皆有可能，异常类问题 迎刃而解
  - 工程中允许各种不合理的事件出现，给它们一个很小的值即可
  - 年龄有负值吗？或者说时间有负值吗？是不是有个概念叫“公元前”？
  - 公元是正的，起点是0，公元前是负值的，可以吗？
  - 以出生为起点，年龄是正的，以成年懂事为起点，那出生是不是就可以是负的？
- 水中可以有鱼吗？
  - 让你取的水，结果是取来的水中还带着小鱼和杂草...
  - 那这水还连续吗？
  - 这其实就是现实，现实是复杂的，你中有我，我中有你，不像理论那么纯粹
- 这数据是来自于实现，所以也不会那么纯粹...

计算量的问题
- 连续型数据是无限的，在处理时，全部都是离散化的数据
- 说白了，虽然走的是连续型变量的计算逻辑，
- 但真正计算时，都是一个个确切的数值在相乘在相加，都是离散的
- 由于计算量的问题，不管连续还是离散在具体计算时都是在计算离散的
- 连续与离散在代码中的区别没那么大


最终的效果
- 这是工程中最关心的问题，核心问题，连续也好，离散也罢，最终效果如何？
- 最终效果差别不大
- 既然效果差不多，那么怎么实现方便怎么来
- 很明显，连续型变量计算使用概率密度图替换，比离散变量的计算逻辑简单多了
- 于是，贝叶斯默认所有变量为连续型变量

这里其实暗含了工程落地的两个大标准
- 条件是什么，什么业务场景？
- 以结果为导向，效果怎么样？

至于中间使用了什么算法，怎么做的，还排这两个后面...

高斯贝叶斯 就是 贝叶斯的 高斯版本
- 朴素：默认特征间相互独立
- 连续：默认变量为连续型变量，并以概率密度图替代概率进行计算

在工程上，在数据量大的情况下
- 一个变量是离散还是连续本质区别不大，就是有差别也不大，可以默认没区别
- 在数据预处理时，比如归一化，将所有数据归到[0,1]
- 一些处理技巧上，就默认把变量当作连续变量处理了，比如取两个离散变量的均值等

高斯贝叶斯适用场景

适用于文本处理，比如NLP领域

在其他场景中，效果不理想...

概念回顾

注意这里说的是概率的分布，所以才会有小于x的概率是多少

如果是概率函数，则会更倾向于求某个值的概率

概率密度函数是概率分布函数的积分，这一点是没有问题的

接下来讨论概率密度函数是不是概率分布函数的导函数，这一点稍微有点分歧

这是来自两个大模型的回答，
其中一个自说是擅长数学推理的，它一直认为存在积分关系即有导函数关系
另外一个大模型则是认中，在不定积分的情况下，积分关系存在导函数关系

离散变量的全体是训练集，某个类型的概率是个体占训练集的比例

连续变量的全体并不是训练集，而是自然界/客观世界中的全体
数据集，包括训练集/测试集 中的数据，只看作单点，是客观世界中的一部分
这意味着，不管你数据集的分布是均匀的还是正态的，还是什么其他的，
都被默认为是正态分布中的一小部分

def p_normal(x, mu, sigma):
    """正态分布的概率密度函数
    - x：变量取值
    - mu：均值
    - sigma：标准差

    exmaples
    -----------------------------
    p_normal(x=0, mu=0, sigma=1)  # 0.3989422804014327

    p_normal(x=np.array([-1,0,1]), mu=0, sigma=1) # array([0.24197072, 0.39894228, 0.24197072])

    - 连续变量计算概率不需要像离散变量那样输入全体变量，因为连续变量的全体是无限的数量

    """
    return 1 / np.sqrt(2 * np.pi) / sigma * np.exp(- ((x - mu)/sigma) ** 2 / 2 )

import numpy as np
from matplotlib import pyplot as plt

x = np.linspace(start=-7,stop=7,num=100)
y = p_normal(x, mu=0, sigma=1)
plt.plot(x,y)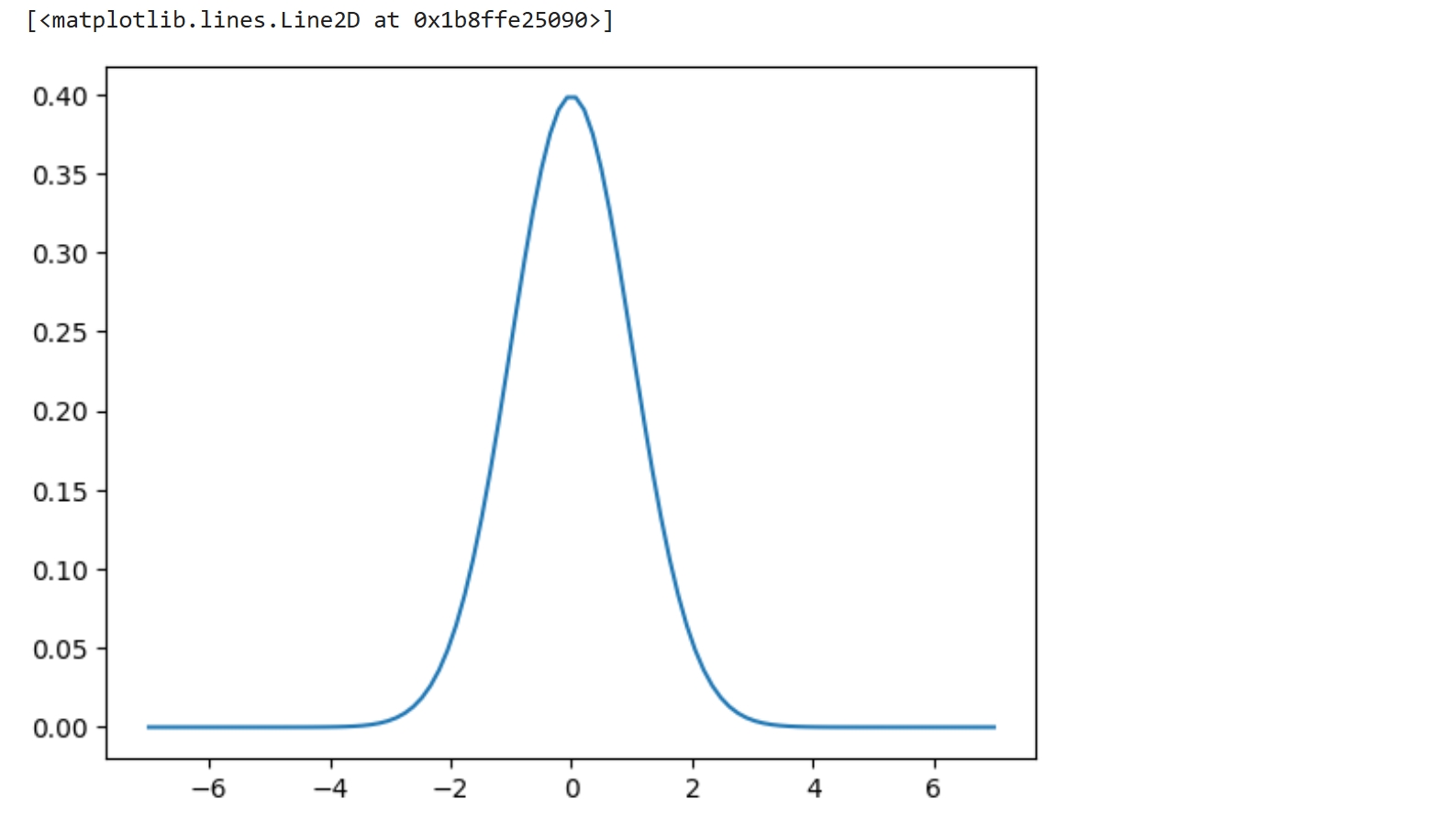

视角：全局视角，不看某个具体的元素，看整体，看所有数据，看整个分布...

均值：平均值，全体数据之和/全体数据个数

标准差：数据偏离中心的平均距离，有的数据离中心很近，也有则很远

均值决定了分布的中心在哪里，标准差则侧重说明数据偏离中心的程度
这两个要素可以描述分布之间的差异/不同

不同的数据有不同的均值与标准差

x1 = np.linspace(start=-7,stop=7,num=100)
x1.mean(),x1.std()   #(-2.842170943040401e-16, 4.0820705117990865)

x2 = np.linspace(start=-7,stop=17,num=100)
x2.mean(),x2.std()   #(5.0, 6.99783516308415)

但若将上面的分布都拉到以0为中心，以1为标准差时，他们的分布就是一样的了

x11 = (x1-x1.mean())/x1.std()
x22 = (x2-x2.mean())/x2.std()
x11.mean().round(6),x11.std(),x22.mean().round(6),x22.std()

减去均值就是去中心，将分布的中心拉到0的位置
除以自身的标准差，就是将分布的标准差归于1，
然后再观察两个分布中元素的差异，就发现他们没有差异，都是均匀分布出来的数据...

x11[:3],x22[:3],
(array([-1.71481604, -1.68017329, -1.64553055]),
 array([-1.71481604, -1.68017329, -1.64553055]))

也这是标准归一化可以起到统一量纲的原因之一

可以理解为，将原生数据统一投影到相同的尺度上，再去比较他们，
会将原生数据的差异转化为同一尺度上的差异，
这样更容易比较，更容易发现一些共性上的差异，也就是本质上的差异

至于说x22的数据普遍比x11大一些，这是表象，本质上x11与x22是同一类数据
比如，大苹果比小苹果大一些，但它们都是苹果，不是西红柿，也不是西瓜...

也就是说，贝叶斯的计算，不需要在数据处理阶段对数据做预处理工作
在计算阶段自带了这一步

(x-mean)/std

并且除以std这个操作，进行两次，一次在e的指数中，
一次是进行完指数函数的计算后，又除了一次std

连续概率的求解，
实际上是先将数据分布拉到了标准正态分布，然后又进一步做了转换

P(yi|x) = P(x|yi)P(yi)

P(x|yi) = P(x1|yi)P(x2|yi)P(x3|yi)...P(xn|yi)

yi是标签中的某一类，计算出所有类别的概率后，取最大类别的概率 作为 样本x的类别

P(yi)    按离散变量概率的求解方式进行计算

P(x1|yi)
- 先从数据集中取出标签yi对应的数据
- 在这些数据中，按连续变量概率的求解方式进行计算x1的概率，即哪怕x1是离散变量也不对x1数数了

  
贝叶斯适用于文本处理，在其他场景则效果不佳，

个人猜测是这种计算方式更适用于
- 连续性相对较强且
- 类别与类别之间差异较大
- 特征极度复杂且多，但重要特征相对集中，不重要特征相对稀疏
的场景

自然语言是描述世界的，实际上只是描述世界中的一个部分，
事物复杂且多，但主要描述的部分，实则集中于一个场景中
大多数特征在所针对的场景中，作用不大