BIRCH原理
|
BIRCH算法解释 BIRCH(Balanced Iterative Reducing and Clustering Using Hierarchies)算法 是一种基于层次聚类的算法,其特点在于能够在大规模数据集上进行高效的聚类操作。 Iterative 英/ˈɪtərətɪv/ 美/ˈɪtəˌreɪtɪv/ 迭代;迭代法;迭代式;反复性;反复式 Hierarchy 英/ˈhaɪərɑːki/ 美/ˈhaɪərɑːrki/ 层次;等级;层级;层次结构;层级命令面板 BIRCH算法通过构建聚类特征树(Clustering Feature Tree,简称CF Tree) 来快速发现数据的聚类结构,这个树结构类似于平衡B+树。 基本原理 BIRCH算法的核心在于聚类特征(Clustering Feature,简称CF)和CF树的构建。 每个CF是一个三元组,包含簇的大小(N)、线性和(LS,即簇内各数据点在每一维上的和) 和 平方和(SS,即簇内各数据点在每一维上的平方和)。 CF树的每一个节点由若干个CF组成,内部节点的CF还有指向子节点的指针, 而所有叶子节点则通过双向链表链接起来。 BIRCH算法通过以下步骤进行聚类: 初始化: 扫描所有数据,建立初始化的CF树,将稠密数据分成簇,稀疏数据作为孤立点处理。 可选优化: 对CF树进行筛选,去除异常CF节点,并利用其他聚类算法(如K-means)对CF元组进行聚类,以优化CF树结构。 聚类: 利用优化后的CF树的所有CF节点的质心,作为初始质心点,对所有的样本点按距离远近进行聚类。 BIRCH算法的聚类过程是基于密度的,它会将数据点分为密集点和稀疏点。 密集点被聚类到一个聚类中心中,而稀疏点则被作为噪声点处理。 聚类结果是一个聚类树,每个节点包含一个聚类中心和一个聚类半径, 聚类半径表示该聚类中心周围的数据点的密度。 应用场景 BIRCH算法在多个领域有广泛的应用,包括但不限于: 推荐系统:通过聚类用户行为和喜好,提供更个性化的推荐。 社交网络分析:在大规模社交网络数据中,通过BIRCH算法可以找出社群结构或关键影响者。 金融风控:用于检测异常交易行为或欺诈行为。 医疗研究:在基因序列、疾病发展等方面进行分群,以便进行更深入的研究。 在乳腺癌数据集的应用中, BIRCH算法可以基于患者的各种特征(如年龄、病理分级、肿瘤大小等)对患者进行聚类, 从而发现不同的患者群体, 这对于疾病的分类、治疗方案的制定以及预后评估都具有重要意义。 与其他聚类算法的对比 与其他聚类算法相比,BIRCH算法具有以下特点: 高效性:BIRCH算法只需要单遍扫描数据集就能进行聚类,运行速度很快。 可扩展性:由于使用了CF树结构,BIRCH算法能有效地处理大规模数据集。 层次结构: 不同于K-means的扁平聚类,BIRCH提供了一种层次聚类结构,这在某些应用场景中可能更有用。 球形假设: BIRCH算法假设簇是球形的,这在某些情况下可能不适用。 相比之下,DBSCAN等算法能够发现任意形状的簇。 对高维数据的效果: BIRCH算法对高维、非凸数据的效果不如一些其他算法(如谱聚类、CLIQUE等), 后者在处理高维数据或复杂形状的数据时更为有效。 综上所述,BIRCH算法是一种高效、可扩展的基于密度的聚类算法, 特别适用于大规模数据集, 但在处理高维、非凸数据时可能不如其他算法。 |
|
|
|
|
|
|
|
|
COPOD
COPOD 异常/离群 检测算法 - 可以理解为输入的数据是一类数据,数据密集处是大多样本呆的地方 - 边缘处零零散散的样本将被认为是不合群的数据 - 中心到最远处的距离定义为1,中间的数据介于[0,1],如此每个样本就有一个分数 - 人工取一个阈值,比如0.95,大于该阈值的样本被认定为离群样本 - 以上是通俗理解,实际上它基于Copula理论,特别适用于高维数据的异常检测 COPOD(Copula-based Outlier Detection)是一种基于Copula理论的异常检测算法, 特别适用于高维数据的异常检测。 它通过将数据特征转换为Copula分布,以捕捉特征之间的相关性,从而有效地检测异常点。 COPOD算法通过计算每个数据点与其邻域之间的不一致性分数来识别异常值。 COPOD的原理 Copula变换: 首先,将数据集中的每个特征通过其边缘分布变换到标准均匀分布。 这一步是通过估计每个特征的累积分布函数(CDF)来实现的。 Copula建模: 使用Copula函数来捕捉特征之间的相关性。 Copula函数可以将多个均匀分布的边缘变量联合成一个多变量分布。 不一致性分数计算: 对于每个数据点,计算其与周围点的不一致性分数。这个分数反映了数据点与其余数据点之间的偏差程度。 异常检测: 根据不一致性分数,设置一个阈值来确定哪些数据点是异常值。 |
import pandas as pd
import numpy as np
import joblib
from pyod.models.copod import COPOD
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import PowerTransformer
class COPODModel():
def init(self):
self.clf = None
def predict_probs(self, X):
self.clf = COPOD(contamination=0.05)
self.clf.fit(np.array(X))
scaler = MinMaxScaler()
copod_scores_2d = self.clf.decision_scores_.reshape(-1,1)
# 分数进行box-cox转换
pt = PowerTransformer(method = 'box-cox')
copod_scores_i_boxcox = pt.fit_transform(copod_scores_2d)
copod_scores_nol = scaler.fit_transform(copod_scores_i_boxcox).flatten()
return copod_scores_nol
from sklearn.preprocessing import StandardScaler
def generate_data(n_normal=100, n_anomalies=10):
normal_data = np.random.normal(loc=0, scale=1, size=(n_normal, 2))
anomaly_data = np.random.normal(loc=5, scale=0.5, size=(n_anomalies, 2))
return np.vstack((normal_data, anomaly_data))
data = generate_data()
# 数据预处理(标准化)
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data)
model = COPODModel() y_probs = model.predict_probs(X = data_scaled) ## 绘图理解 - 取阈值 - 图形展示大于阈值的数据,会被标记为红色 threshold= 0.95
import matplotlib.pyplot as plt
# 确定异常标签(高于阈值的为异常值)
labels = ((y_probs > threshold)).astype(int)
# 绘制结果
plt.scatter(data[:, 0], data[:, 1], c=labels, cmap='coolwarm', marker='o', edgecolor='k')
plt.colorbar(label='Outlier Labels (1: anomaly, 0: normal)')
plt.title('COPOD for Anomaly Detection')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()
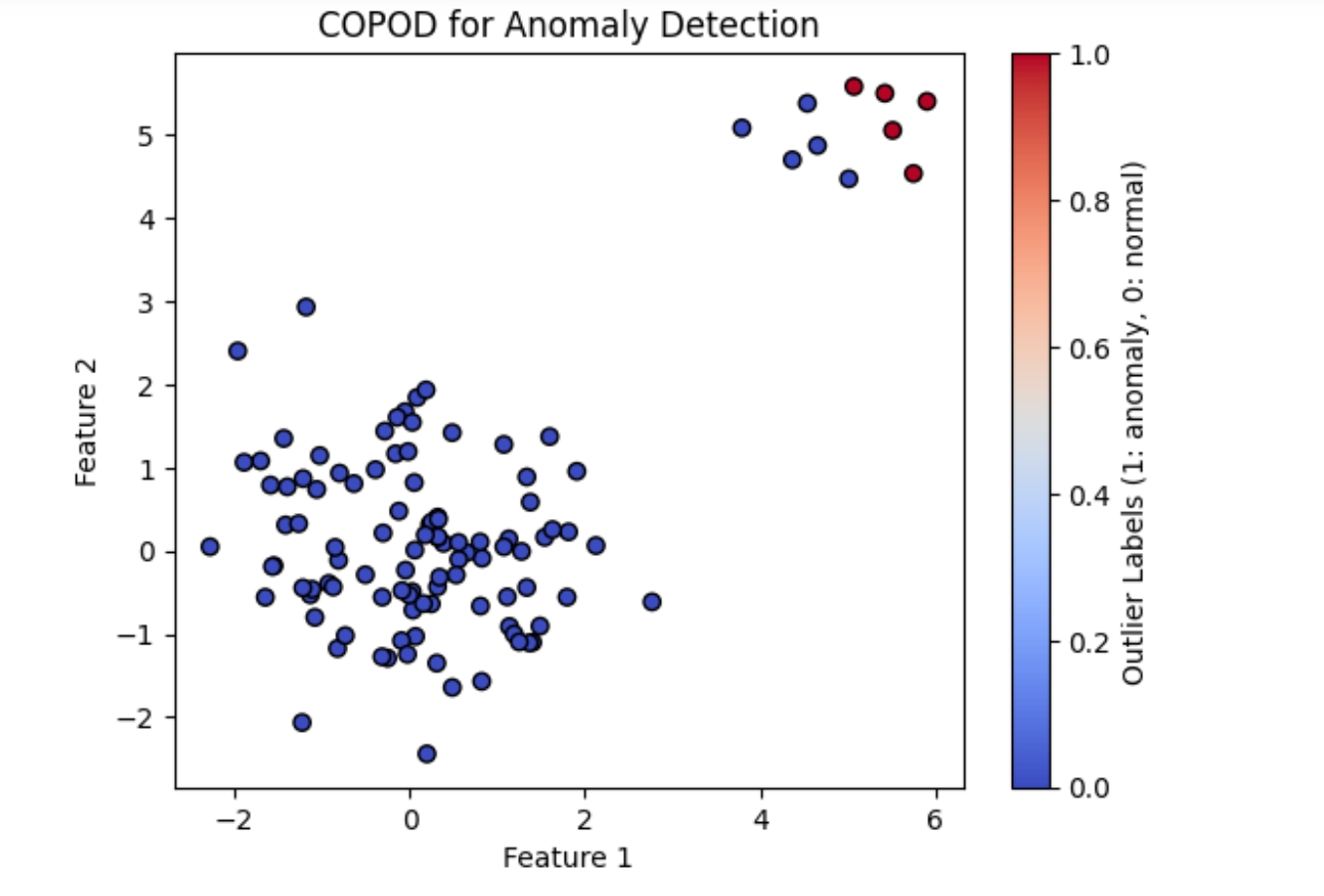
实际上,COPOD算法并不是一个可以直接通过pip安装的库,而是一个算法概念。 在Python中,没有官方或广泛认可的名为“copod”的包来直接实现这个算法。 此例中 - COPOD主要是为每个样本打分,哪些是离群样本,更多的依赖于阈值的确定 - 阈值的确定完全依赖于业务数据,因此本例中模型只负责输出样本的分数 |
COPOD 算法 COPOD(Copula-based POD)是一种基于copula theory的主成分分析(Principal Component Analysis,PCA)算法。它可以用于降维、数据可视化和异常检测等任务。 原理 COPOD 算法的核心思想是将原始数据转换为copula space,然后使用 POD 算法对 copula space 进行降维。copula space 是一个高维空间,其中每个点表示一个数据样本的copula分布。 首先,我们需要计算原始数据的copula分布。 copula 是一个概率分布,它描述了随机变量之间的依赖关系。 COPOD 算法使用 Gaussian copula 作为默认的copula分布。 然后,我们将原始数据转换为copula space。 对于每个数据样本,我们计算其copula分布,然后将其转换为copula space 中的点。 最后,我们使用 POD 算法对 copula space 进行降维。 POD 算法可以将高维空间降维到低维空间,使得降维后的空间保留原始数据的主要特征。 核心参数 COPOD 算法有两个核心参数: n_components:指定降维后的维数。 copula_type:指定copula分布的类型。默认为 Gaussian copula。 降维 分布转换
COPOD(Copula-based Outlier Detection)是一种基于Copula的无监督异常检测算法。以下是对COPOD原理及其与其他无监督算法主要区别的详细阐述:
一、COPOD的原理
COPOD算法的核心思想是利用Copula函数来捕捉数据特征之间的依赖关系,并基于这些关系来评估数据点的异常程度。具体来说,COPOD算法通过以下步骤实现异常检测:
数据预处理:首先对数据进行预处理,包括标准化或归一化等,以确保不同特征之间具有可比性。
Copula变换:接着,利用Copula函数对数据进行变换。Copula函数是一种能够捕捉变量之间依赖关系的工具,它能够将多维数据的联合分布分解为各个变量的边缘分布和一个Copula函数。通过Copula变换,可以得到一个与原始数据具有相同依赖结构但边缘分布为均匀分布的新数据集。
计算局部密度:然后,计算每个数据点在新数据集中的局部密度。局部密度反映了数据点与其周围数据点的相似程度,可以通过计算数据点与其邻居之间的距离或相似度来得到。
评估异常程度:最后,根据局部密度来评估数据点的异常程度。局部密度越低的数据点被认为是异常点的可能性越大。具体来说,COPOD算法通过计算每个数据点的局部密度与整个数据集平均局部密度的比值来得到一个异常得分,异常得分越高表示数据点越异常。
二、COPOD与其他无监督算法的主要区别
异常检测机制:
COPOD:基于Copula函数来捕捉数据特征之间的依赖关系,并基于这些关系来评估数据点的异常程度。它利用局部密度来识别异常点,局部密度越低的数据点被认为是异常点的可能性越大。
其他无监督算法(如K-means聚类、DBSCAN等):主要通过聚类来发现数据中的模式或结构,并基于聚类结果来评估数据点的异常程度。它们通常根据数据点与聚类中心或聚类边界的距离来判断数据点是否异常。
数据适应性:
COPOD:对数据中的非线性关系和复杂依赖结构具有较好的适应性。它通过Copula变换来捕捉这些关系,并能够处理具有不同尺度和分布的特征。
其他无监督算法:在某些情况下可能对数据中的非线性关系和复杂依赖结构不够敏感,导致异常检测效果不佳。特别是当数据特征之间具有复杂的依赖关系时,这些算法可能无法准确捕捉这些关系。
计算复杂度:
COPOD:计算复杂度较高,因为它需要计算每个数据点的局部密度,这涉及大量的距离计算或相似度计算。
然而,随着计算技术的发展和算法的优化,这个问题正在逐渐得到解决。
其他无监督算法:计算复杂度因算法而异。
例如,K-means聚类算法具有较低的计算复杂度,但可能受到初始聚类中心选择和聚类数目设置的影响;
而DBSCAN算法则具有较高的计算复杂度,因为它需要计算每个数据点与所有其他数据点之间的距离。
应用场景: COPOD:适用于处理具有复杂依赖关系和不同尺度特征的数据集, 特别是在金融、医疗和网络安全等领域中的异常检测任务中表现出色。 其他无监督算法:适用于不同的应用场景。 例如,K-means聚类算法常用于市场细分、客户分类和图像分割等领域; DBSCAN算法则常用于空间数据挖掘和图像分析等领域。 综上所述,COPOD算法在异常检测方面具有较高的准确性和适应性, 特别适用于处理具有复杂依赖关系和不同尺度特征的数据集。 然而,它也存在计算复杂度较高的问题,需要在实际应用中根据具体需求和数据特点进行选择和优化。 |
COPOD(Copula-Based Outlier Detection) 是一种基于copula理论的无监督异常检测算法,适用于高维数据。 它通过构建数据特征的copula函数来捕捉特征间的依赖关系,从而有效地检测异常点。 Init signature: COPOD(contamination=0.1, n_jobs=1) Docstring: COPOD class for Copula Based Outlier Detector. COPOD is a parameter-free, highly interpretable outlier detection algorithm based on empirical copula models. See :cite:`li2020copod` for details.
Parameters
----------
contamination : float in (0., 0.5), optional (default=0.1)
The amount of contamination of the data set, i.e.
the proportion of outliers in the data set. Used when fitting to
define the threshold on the decision function.
n_jobs : optional (default=1)
The number of jobs to run in parallel for both `fit` and
`predict`. If -1, then the number of jobs is set to the
number of cores.
contamination 含义: 这个参数指定了数据集中异常点的预期比例。 它用于在训练过程中指导算法,以识别出相应比例的异常点。 取值范围: 通常在0到0.5之间,具体取值取决于数据集中异常点的实际比例。 影响: contamination的值直接影响算法对异常点的判断标准。 设置过低可能导致一些真正的异常点被误判为正常点,设置过高则可能导致正常点被误判为异常点。 |
|
|
参考