HMM概述

HMM是什么

 
双序列事件：
序列1相互独立
序列2存在前后依赖关系
序列1的每个事件的发生由序列2对应的事件决定

HMM是双重随机过程形成的两个序列：一个叫观测序列，一个叫隐藏序列，满足以下三个条件：
观测序列的事件相互独立，
隐藏序列的事件(这里叫状态)仅前后存在依赖关系 
观测序列事件发生的概率由隐藏序列对应的状态决定，观测序列与隐藏序列事件一一对应 

观测：已有统计数据，观察到的统计数据，容易得到或已知数据
隐藏：有了部分数据，不那么容易直接拿到，需要拿到，需要训练个模型预测的数据 


https://hmmlearn.readthedocs.io/en/latest/index.html 

 
状态序列：
  - 初始状态概率矩阵：各个状态最初的概率
  - 状态转移矩阵：一个状态到另外一个状态的概率
观察序列：
  - 发射概率矩阵：各个状态下，观察序列元素的概率分布

HMM算法在行业中的应用

 
隐马尔可夫模型（HMM）：是结构最简单的动态贝叶斯网络，是一种尤其著名的有向图结构，

主要用于时序数据的建模，在语音识别、自然语言处理等领域有广泛应用，

在分词算法中，隐马尔可夫经常用作能够发现新词的算法，
通过海量的数据学习，能够将人名、地名、互联网上的新词等一一识别出来，具有广泛的应用场景。

HMM五元组

 
观测序列——O(observe)
隐藏状态序列——I 
初始状态概率——π
状态转移矩阵——A
观测概率矩阵——B（也叫发射概率）

两个基本假设： 
1. 齐次马尔科夫性假设：在t时刻的状态只依赖于t-1时刻的状态 
2. 观测独立性假设：在任一时刻的观测只依赖于该时刻的状态

有向图中的序列

 
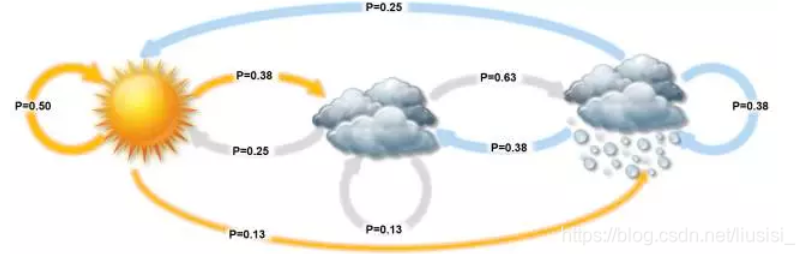
状态是有向图，相互关联的状态形成一个网，那状态序列怎么来的？ 

状态序列是由观察序列得来的，通过观测得到一个序列，每个观测属于一个状态，
这样就有了状态序列 

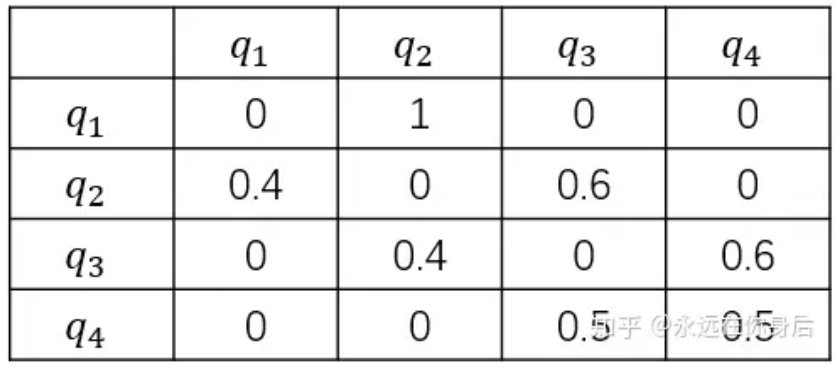
状态转移矩阵——A

 
状态转移矩阵必是方阵，状态s1永远都不可能转移到状态s3，则标记为0 
每个状态转移到的状态可以是自己，也可以是其他状态 
每个状态转移出去各个的概率和为1 

HMM解决三类问题

 
给定模型参数和观测数据，估计隐藏状态的最佳序列。

给定模型参数和观测数据，计算模型似然度。

仅给定观察到的数据，估计模型参数。

HMM示例

 
import numpy as np 
from hmmlearn import hmm

#观测序列
obs = np.array([0,1,0,1,0,0,1,1,1,0]).reshape(-1,1)

model=hmm.GaussianHMM(n_components=2, covariance_type="full", n_iter=100)

# model.startprob_  = np.array([0.6,0.4])  #初始状态概率 
# model.transmat_ = np.array([[0.7,0.3],[0.4,0.6]]) # 状态转移概率矩阵
model.emissionprob_ = np.array([[0.8,0.2],[0.3,0.7]]) #观测概率矩阵

#使用观测序列训练 
model.fit(obs)

#预测隐藏状态序列
hidden_states = model.predict(X=obs)
hidden_states
array([0, 1, 0, 1, 0, 0, 1, 1, 1, 0])

init_params='mc'

 
init_params默认为stmc 
Can contain any combination
of 's' for startprob, 't' for transmat, 'm' for means, and 'c' forcovars.  Defaults to all parameters.

去掉st，然后手工指定 初始状态概率 和 状态转移概率矩阵

 
import numpy as np 
from hmmlearn import hmm

#观测序列
obs = np.array([0,1,0,1,0,0,1,1,1,0]).reshape(-1,1)

model=hmm.GaussianHMM(n_components=2, covariance_type="full", n_iter=100,init_params='mc')

model.startprob_  = np.array([0.6,0.4])  #初始状态概率 
model.transmat_ = np.array([[0.7,0.3],[0.4,0.6]]) # 状态转移概率矩阵
model.emissionprob_ = np.array([[0.8,0.2],[0.3,0.7]]) #观测概率矩阵

#使用观测序列训练 
model.fit(obs)

#预测隐藏状态序列
hidden_states = model.predict(X=obs)
hidden_states
array([1, 0, 1, 0, 1, 1, 0, 0, 0, 1])

参考

    机器学习 HMM 
    HMM（隐马尔可夫）简介
    一站式解决：隐马尔可夫模型（HMM）全过程推导及实现 
    隐马尔可夫模型（HMM）