线性回归
线性回归(Linear Regression)算法是一种用于预测连续值变量的统计方法。 其基本原理是通过寻找自变量(解释变量、特征)和因变量(响应变量、目标)之间的最佳线性关系, 来建立一个数学模型,以便使用这个模型对新的自变量值进行预测。 线性回归的原理 线性回归模型假设目标变量(y)与一个或多个解释变量(x1,x2,...,xn)之间存在线性关系, 即可以用一个线性方程来描述它们之间的关系: y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_n x_n + \epsilon \] 其中,$\beta_0$ 是截距项, $\beta_1, \beta_2, ..., \beta_n$ 是回归系数(也称为斜率或权重), 它们表示了当其他解释变量保持不变时,某个解释变量每变化一个单位,目标变量平均会变化多少。 $\epsilon$ 是误差项,表示了模型无法解释的变异部分。 为了找到最佳的回归系数,线性回归算法通常采用最小二乘法(Least Squares Method)来拟合数据。 最小二乘法的目标是找到一组回归系数, 使得预测值与实际值之间的差的平方和(即残差平方和)最小。 这通常涉及到求解一个线性方程组或优化问题 |
|
回归二字的含义 “回归”一词最初来源于高尔顿(Francis Galton)在19世纪对遗传学的研究。 他观察到,虽然父母的身高会影响子女的身高,但子女的身高会趋向于整个人群的平均身高, 即存在一种“回归平均”的现象。 后来,统计学家们将这一概念应用到数据分析中, 用来描述因变量(响应变量)随自变量(解释变量)变化的趋势或规律, 并通过建立数学模型来预测因变量的值。 在统计学中,“回归”通常指的是通过拟合一个函数(如线性函数、多项式函数等) 来描述自变量和因变量之间关系的过程。 这个过程既可以是预测性的(即使用模型来预测新的数据点), 也可以是解释性的(即使用模型来解释自变量和因变量之间的关系)。 因此,在线性回归中, “回归”二字指的是通过建立一个线性模型来拟合自变量和因变量之间的关系, 并使用这个模型来进行预测或解释的过程。 |
|
|
|
|
|
|
逻辑回归
|
逻辑回归API示例 from ai.datasets import load_hotel X_train,y_train,X_test,y_test = load_hotel(return_dict=False, return_Xy=True) X_train: (4800, 85) y_train: (4800,) X_test: (1200, 85) y_test: (1200,) from sklearn.linear_model import LogisticRegression model = LogisticRegression(max_iter=10000) model.fit(X=X_train,y=y_train) model.score(X=X_test,y=y_test) 0.6008333333333333 y_pred = model.predict(X=X_test) y_pred[:10] array([0, 0, 1, 1, 0, 1, 1, 0, 0, 0]) |
机器学习算法中的逻辑回归(Logistic Regression)是一种广泛应用于分类问题的算法, 尽管其名称中包含“回归”, 但实际上它主要用于处理分类任务,特别是二分类问题。 逻辑回归的原理可以概括为以下几个关键点: 逻辑回归通过建立一个预测函数(通常是线性函数)来预测输入变量与输出类别之间的关系。 然而,与线性回归直接输出连续值不同, 逻辑回归通过引入Sigmoid函数(也称为逻辑函数)将线性回归的输出转换为概率值, 从而进行分类。 逻辑回归(Logistic Regression)是一种广泛应用的分类算法,尤其是在二分类问题中。 其核心在于使用一个逻辑函数(通常是sigmoid函数) 将线性回归的输出映射到(0, 1)的区间内, 从而表示一个概率值。 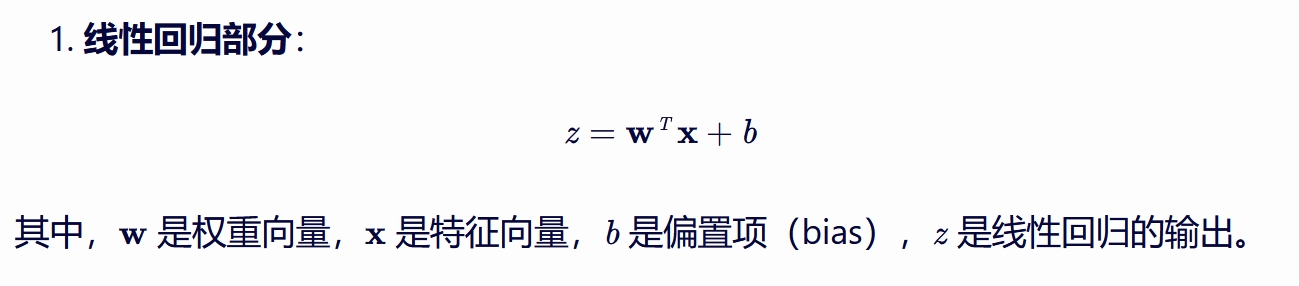



优化: 逻辑回归通过梯度下降等优化算法来最小化损失函数,从而更新权重 w 和偏置 b 说白了,逻辑回归就相当于单层的神经网络 |
|
|
|
|
|
|
逻辑回归·自定义
import numpy as np
class Linear_Regression:
def __init__(self):
self._w = None
def fit(self, X, y, lr=0.01, epsilon=0.01, epoch=1000):
#训练数据
#将输入的X,y转换为numpy数组
X, y = np.asarray(X, np.float32), np.asarray(y, np.float32)
#给X增加一列常数项
X=np.hstack((X,np.ones((X.shape[0],1))))
#初始化w
self._w = np.zeros((X.shape[1],1))
for _ in range(epoch):
#随机选择一组样本计算梯度
random_num=np.random.choice(len(X))
x_random=X[random_num].reshape(1,2)
y_random=y[random_num]
gradient=(x_random.T)*(np.dot(x_random,self._w)-y_random)
#如果收敛,那么停止迭代
if (np.abs(self._w-lr*gradient)<epsilon).all():
break
#否则,更新w
else:
self._w =self._w-lr*gradient
return self._w
def print_results(self):
print("参数w:{}".format(self._w))
print("回归拟合线:y={}x+{}".format(self._w[0],self._w[1]))
def predict(self,x):
x=np.asarray(x, np.float32)
x=x.reshape(x.shape[0],1)
x=np.hstack((x,np.ones((x.shape[0],1))))
return np.dot(x,self._w)
import pickle
#创建数据
x=np.linspace(0,100,10).reshape(10,1)
rng=np.random.RandomState(4)
noise=rng.randint(-10,10,size=(10,1))*4
y=4*x+4+noise
model=Linear_Regression()
model.fit(x,y,lr=0.0001,epsilon=0.001,epoch=20)
with open('model.pickle', 'wb') as file:
pickle.dump(model, file)
with open('model.pickle', 'rb') as file:
model=pickle.load(file)
print(model.predict([50]))
model.print_results()
|
参数说明
LR(逻辑回归)算法的重要参数主要包括以下几个方面:
一、正则化相关参数
C:正则化强度的倒数,是一个浮点数。C的值越小,正则化强度越大,模型越简单,从而有助于防止过拟合。C的默认值通常为1.0,但在实际应用中,可能会根据具体的数据集和任务需求进行调整。调整C的值时,通常会在10的幂次方上进行尝试,如0.01、0.1、1、10、100等。
penalty:正则化类型,用于指定模型使用的正则化方法。逻辑回归默认使用L2正则化,但也可以选择L1正则化。L1正则化有助于特征选择,因为它可以将一些系数缩减为零。而L2正则化则主要用于缩减系数的大小,但不会将它们设置为零。
二、优化算法相关参数
solver:用于指明损失函数的优化方法。不同的求解器具有不同的优缺点和特性,会产生不同的结果。常见的求解器包括‘liblinear’、‘newton-cg’、‘lbfgs’和‘sag’等。其中,‘liblinear’适用于小数据集,而‘newton-cg’、‘lbfgs’和‘sag’则适用于大数据集。需要注意的是,如果选择了L1正则化,则只能使用‘liblinear’求解器,因为其他求解器需要损失函数的一阶或二阶连续导数,而L1正则化的损失函数不是连续可导的。
tol:残差收敛条件,用于控制优化算法的停止条件。当两步之间的残差小于tol时,算法会停止迭代。默认值通常为0.0001,但可以根据具体需求进行调整。
max_iter:算法收敛的最大迭代次数。如果算法在达到最大迭代次数之前仍未收敛,则会停止迭代。默认值通常为100,但也可以根据具体需求进行调整。
三、模型其他参数
fit_intercept:是否将截距/方差加入到决策模型中。默认为True,表示将截距加入到模型中。如果设置为False,则模型不会计算截距。
class_weight:用于调节正负样本比例的参数。默认值为None,表示正负样本的权重是一样的。如果数据集存在类别不平衡问题,可以通过设置class_weight来调节正负样本的权重,从而改善模型的性能。例如,可以设置为“balanced”,让模型根据正负样本的绝对数量比来自动设定权重比。
random_state:随机种子的设置。如果设置了随机种子,则每次运行代码时都会得到相同的结果。这对于实验的可重复性非常重要。默认值为None,表示每次运行代码时都会使用不同的随机种子。
multi_class:分类方法参数选择。对于二分类问题,这个参数的设置不会影响结果。但在多分类问题中,可以选择“ovr”(一对多)或“multinomial”(多项式)方法。默认值为“ovr”。
verbose:是否输出模型运算过程中的一些信息。默认为False,表示不输出。如果设置为True,则会输出一些冗余信息,有助于了解模型的训练过程。
warm_start:是否使用上次的模型结果作为初始化。默认为False,表示不使用。如果设置为True,则会利用上次的模型结果作为初始化,从而加速模型的训练过程。但需要注意的是,如果更改了模型的其他参数(如C、penalty等),则warm_start可能会失效。
n_jobs:并行运算数量(核的数量)。默认为1,表示使用单个核心进行运算。如果设置为-1,则表示使用所有可用的核心进行并行运算,从而加速模型的训练过程。
综上所述,LR逻辑回归算法的重要参数包括正则化相关参数(C、penalty)、优化算法相关参数(solver、tol、max_iter)以及模型其他参数(fit_intercept、class_weight、random_state、multi_class、verbose、warm_start、n_jobs)。这些参数的设置会直接影响模型的性能和训练过程,因此需要根据具体的数据集和任务需求进行仔细调整。
|
import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# 加载乳腺癌数据集
data = load_breast_cancer()
X = data.data
y = data.target
# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 设置逻辑回归模型的参数
lr_params = {
'C': 1.0, # 正则化强度的倒数
'penalty': 'l2', # 正则化类型,'l1'或'l2'
'solver': 'liblinear', # 优化算法,适用于小数据集和L1正则化
'tol': 0.0001, # 残差收敛条件
'max_iter': 100, # 最大迭代次数
'fit_intercept': True, # 是否计算截距
'class_weight': None, # 类别权重,None表示自动平衡,或指定为字典形式
'random_state': 42, # 随机种子,保证结果可复现
'multi_class': 'ovr', # 多分类策略,'ovr'表示一对多,'multinomial'表示多项式
'verbose': 0, # 是否输出训练过程信息,0表示不输出
'warm_start': False, # 是否使用上次的模型结果作为初始化
'n_jobs': -1 # 并行任务数,-1表示使用所有处理器核心
}
# 创建逻辑回归模型实例并训练模型
lr = LogisticRegression(**lr_params)
lr.fit(X_train, y_train)
# 使用测试集进行预测
y_pred = lr.predict(X_test)
# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f'Test Accuracy: {accuracy:.4f}')
# 注意:在实际应用中,可能需要根据数据集和任务需求调整上述参数。
# 例如,可以尝试不同的C值、penalty类型、solver等,以找到最佳的模型配置。
|
fit_intercept参数在逻辑回归(以及线性回归)模型中起着决定是否需要计算截距项的作用。以下是加入与不加入fit_intercept参数的具体区别:
加入fit_intercept=True(默认值)
作用:模型会计算并包含一个截距项(通常表示为b或intercept_)。这意味着模型假设当自变量(特征)全为0时,因变量(目标变量)有一个非零的期望值。
适用场景:在大多数情况下,特别是当数据没有预先中心化(即数据的均值不为0)时,应该包含截距项。这有助于模型更好地拟合数据,因为截距项可以捕捉到数据中可能存在的全局偏移。
数学表达:模型的形式为 y = Xβ + b,其中X是特征矩阵,β是系数向量,b是截距项。
不加入fit_intercept=False
作用:模型不会计算截距项,即假设当自变量全为0时,因变量的期望值为0。
适用场景:在某些特定情况下,如果数据已经预先中心化(即数据的均值为0),或者当你知道截距项不应该被包含在模型中时(例如,在某些设计实验或特定领域知识指导下),可以选择不包含截距项。
数学表达:模型的形式简化为 y = Xβ,其中X和β的含义与上面相同,但没有截距项b。
注意事项
当fit_intercept设置为False时,如果数据实际上没有中心化,这可能会导致模型拟合效果不佳,因为模型无法捕捉到数据中可能存在的全局偏移。
在某些算法实现中,如果fit_intercept设置为False,则normalize参数(如果可用)可能会被忽略,因为标准化通常与包含截距项一起使用。然而,这取决于具体的算法实现。
综上所述,fit_intercept参数的选择取决于数据的特性和模型的需求。在大多数情况下,默认包含截距项是一个合理的选择。但在特定情况下,如果数据已经中心化或你知道截距项不应该被包含,则可以选择不包含截距项。
|
在逻辑回归(Logistic Regression,简称LR)中,
solver参数用于指定损失函数的优化方法,
其可选值包括"newton-cg"、"lbfgs"、"sag"等,这些优化方法在处理大数据集时各有特点。
以下是它们的区别:
一、基本原理
newton-cg(牛顿-共轭梯度法)
使用牛顿法的框架,需要计算Hessian矩阵或其逆矩阵。
采用共轭梯度法来近似求解Hessian矩阵的逆方向的乘积,从而避免了直接计算Hessian矩阵。
lbfgs(有限内存的Broyden-Fletcher-Goldfarb-Shanno算法)
一种改良的拟牛顿方法,不直接使用Hessian矩阵。
使用低秩更新的方式来近似Hessian矩阵的逆,仅保存最近几步的更新信息(如梯度和变量差),通过这些信息构建Hessian矩阵的逆的近似,从而大大减少内存需求。
sag(随机平均梯度下降)
梯度下降法的变种,每次迭代仅使用一部分样本来计算梯度。
适用于样本数据多的情况,是一种线性收敛算法,速度远比普通的梯度下降法快。
二、适用场景与特点
newton-cg
适用于Hessian矩阵稀疏且结构良好的优化问题。
收敛速度通常比梯度下降法和简单的牛顿法要快,尤其是接近最优解时。
在变量数量较多时,计算可能非常昂贵,因为共轭梯度法本身在某些问题上可能会有较慢的收敛速度。
lbfgs
特别适用于大规模问题,平衡了收敛速度和内存使用。
通常比全Hessian方法更快,尤其是在变量数量非常大的情况下。
在实际应用中通常能提供稳定的收敛性能,尤其是在目标函数较为复杂或参数维度较高的情况下。
sag
非常适合于大数据集,因为每次迭代仅使用部分样本来更新梯度,从而加快了计算速度。
不能用于没有连续导数的L1正则化,只能用于L2正则化。
当样本量少的时候不要选择它。
三、正则化支持
newton-cg和lbfgs:只能用于L2正则化,因为L1正则化的损失函数不是连续可导的。
sag:同样只能用于L2正则化。
四、其他注意事项
在sklearn的逻辑回归模型中,从0.22版本开始,solver的默认值从"liblinear"改为"lbfgs",这反映了"lbfgs"在处理大规模数据集时的优势。
在选择solver时,还需要考虑其他参数,如正则化参数、迭代次数、分类方式等,这些参数的选择也会影响模型的性能和结果。
综上所述,在LR中,"newton-cg"、"lbfgs"、"sag"等solver参数在处理大数据集时各有优劣。选择哪种优化方法取决于具体问题的特性,包括问题的规模、Hessian矩阵的特性、内存限制以及对正则化的需求等因素。
|
|
|
参考
sklearn2pmml github
PMML讲解及使用