主成分分析 
使用SVD提取主要信息
    

 
适用于稀疏矩阵 ，就是存在大量0数据的矩阵 
从这样的矩阵中提取主要信息 

如果一个矩阵是稠密的，全是主要信息，那么就不适合使用PCA
    

 
numpy中 二维·矩阵·分解 中详细讲解了矩阵分解及SVD相关的知识，这就主要说PCA 
    

 
U,S,V = np.linalg.svd(A) 

矩阵A@矩阵V的转置 即可实现降维

U中的列与S对应，V中的行与S对应，V转置后变为其列与S对应

一列就是一个维度的计算，取多少列，就会生成多少维，少生成点列，就是降维... 

 
打开IDE,本人使用的是vscode，输入下面的代码，前提是已配置好python环境
from sklearn.decomposition import PCA

按下Ctrl键，鼠标点击PCA,就是去查看源码
    
class PCA(_BasePCA):
    """Principal component analysis (PCA).

    Linear dimensionality reduction using Singular Value Decomposition of the
    data to project it to a lower dimensional space. The input data is centered
    but not scaled for each feature before applying the SVD.
    ... 
    ...
    ...
    """
基于奇异值分解的线性降维
Linear dimensionality reduction using Singular Value Decomposition
一种线性降维方式，使用SVD
    

 
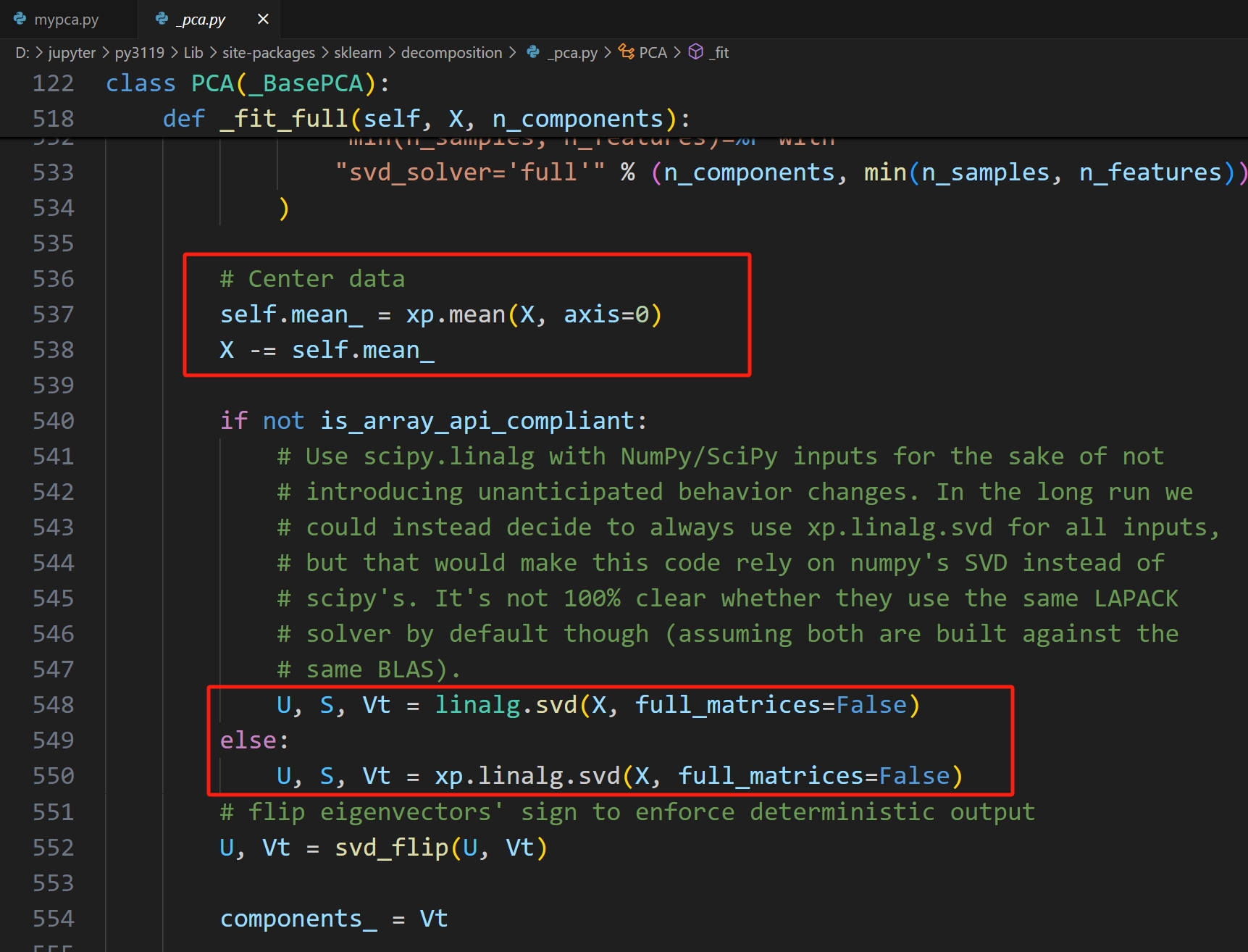
从源码中可以看出，PCA主要依赖于SVD的实现
    

使用同一算法，数据降维前与降维后进行对比

 
import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split

# 加载数据集
X, y = load_breast_cancer(return_X_y=True)
# 切分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,random_state=73)

 
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X=X_train,y=y_train)
knn.score(X=X_test,y=y_test)  # 0.9035087719298246

 
0.9035087719298246
    

 
import pandas as pd
from sklearn.datasets import load_breast_cancer
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler

# 加载乳腺癌数据集
data = load_breast_cancer()
X = pd.DataFrame(data.data, columns=data.feature_names)
y = pd.Series(data.target)

# 数据预处理
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 使用PCA进行降维
pca = PCA(n_components=2)  # 将数据降维到2维
X_pca = pca.fit_transform(X_scaled)

# 输出降维后的数据
print(X_pca)
    

 
# 切分数据集
X_train, X_test, y_train, y_test = train_test_split(X_pca, y, test_size=0.2,random_state=73)

knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X=X_train,y=y_train)
knn.score(X=X_test,y=y_test)  # 0.9035087719298246

 
0.9122807017543859
    

 
# 加载数据集
X, y = load_breast_cancer(return_X_y=True)

# 切分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,random_state=73)

 
class MyPCA(object):
    """
        自定义PCA
    """
    
    def __init__(self, n_components=None):
        """
            挂载超参数
        """
        self.n_components = n_components
    
    def fit(self, X):
        """
            训练过程
        """
        # 转 Numpy 数组
        X = np.array(X)
        
        # 进行 SVD 分解
        U, S, VT = np.linalg.svd(a=X, full_matrices=False)
        
        # 获取转换矩阵
        self.V = VT[:self.n_components, :].T
               
    
    def transform(self, X):
        """降维转换
        - 起名transform是因为在sklearn中无监督学习的命名都是transform
        - 比如StandardScaler，MinMaxScaler就可以先fit,再transform
            
        """
        # 转为 numpy 数组
        X = np.array(X)
        
        # 进行降维操作
        return X @ self.V
    

 
# 构建模型
my_pca = MyPCA(n_components=3)

# 模型训练
my_pca.fit(X=X_train)

# 训练集降维
X_train1 = my_pca.transform(X=X_train)
print(X_train.shape, X_train1.shape)

# 测试集降维
X_test1 = my_pca.transform(X=X_test)
print(X_test.shape, X_test1.shape)
    

 
(455, 30) (455, 3)
(114, 30) (114, 3)
    

 
# 构建模型
knn1 = KNeighborsClassifier(n_neighbors=3)

# 训练模型
knn1.fit(X=X_train1, y=y_train)

# 模型预测
knn1.score(X=X_test1, y=y_test)

 
0.9122807017543859
    

对全体数据集进行降维

 
# 使用PCA进行降维
pca = PCA(n_components=2)  # 将数据降维到2维
X_pca = pca.fit_transform(X_scaled)
    

先对训练集降维学习，再对训练集与预测集的全体进行降维

 
# 构建模型
my_pca = MyPCA(n_components=3)

# 模型训练
my_pca.fit(X=X_train)

# 训练集降维
X_train1 = my_pca.transform(X=X_train)
print(X_train.shape, X_train1.shape)

# 测试集降维
X_test1 = my_pca.transform(X=X_test)
print(X_test.shape, X_test1.shape)
    

 
PCA是无监督的，即降维这个操作不需要标签

但PCA仍然是需要学习，需要训练的 

由于训练集已经是包含上所有的数据规律，
那么在训练集上提取主成份，还是在全体数据集上提取主成分，
其区别应该不大，意思是这两种操作都可以
    

 
PCA的全称是Principal Component Analysis，即主成分分析。

它的主成分由SVD方法确定 

 
# 进行 SVD 分解
U, S, VT = np.linalg.svd(a=X, full_matrices=False)

# 获取转换矩阵
self.V = VT[:self.n_components, :].T
  

 
full_matrices=False 指修减矩阵，使矩阵的形状与self.n_components相符，
即指U,VT不再是原来的样子，也不会对S形成的对角阵补0，只是去减U的列，VT的行  
  

 
S就是主成分，其元素与U的行对应，与VT的行对应 
S的元素由大到小排列 

即最主要的特征放在前面，
U的前面的几列，VT前面的几行 是重要的数据特征，
越往后，其信息越不重要 

主成分是无监督的

 
比如人是复杂的，但要是去相亲(即转化为有监督，标签是相亲满意度或者否成功)
主成分可能是 身材，颜值，收入，资产，地位等

但要是去面试一个AI算法工程师(即转化为有监督，标签是面试是否通过)，
主成分可能是 工作年限，行业，资历，年龄，期望薪水等

人还是同一个人，但由于打的标签不一样，有监督会以标签为目标调整算法中的参数

而PCA不是这样的，PCA不看标签 
它以数据本身的信息为前提，提取其中的主要信息 

PCA是弱化了数据信息中不重要的成分，提取了信息的主要内容 
如何划定哪些信息是次要的，哪些信息是主要的，由SVD算法处理...涉及矩阵论，不是数学天才莫看此书... 
这个过程不用初学者理会，
  

 
比如，
你是一个面试官，要选一批AI算法工程师，虽然面试者提供的信息很多，
但你主要看 工作年限，行业，资历，年龄，期望薪水 这五个就够了
  

 
# 获取转换矩阵
self.V = VT[:self.n_components, :].T
      
比如提取前3个主成分
self.V = VT[:3, :].T

得到的是一个n行3列的矩阵，n就是向量的维度，
不管是训练集，预测集，还是单个样本向量，有n维 

[m行，n列]@[n行，3列] = [m行，3列]
  
即提取前3个主成分，就能得到3列数据，
一个主成分生成一个维度的数据，
3个主成分共生成3份数据，即3个维度的数据，这就降为3维了

 
主成分提取，从大量信息中提取部分主要信息 
适用于原矩阵是稀疏矩阵，特征多且有很多不重要的 

如果特征少或每个特征都很重要，就不适用用PCA